The Non-Destruction of the European Jews

As will be demonstrated, more people died in Ted Kennedy's car at Chappaquiddick than in any "gas chambers" built for extermination in Poland, Germany, or any other German-held territory throughout World War Two. There never was any program to "exterminate" the Jews. The idea was initially conceived by Jewish rabbis, eagerly seized upon by wartime propagandists, and parroted by paranoid conspiracy theorists.

The following rebuttal of the infamous myth is almost redundant, since the "Holocaust" Hoax is already well into its death throes, for example, with Hoaxers having to resort to employing a young woman to pose as a gormless, brainwashed dreamer who digs at a Polish cemetery, finds 40 bone fragments and imagines she's discovered "mass graves" at Treblinka (after no one else was able to find mass graves after 70 years of trying!!!), and to find tiles with a pierced mullet star that is actually a brand mark of a 125-year-old porcelain factory in Poland, to assume that it's a "Star of David", and conclude that it's evidence of "gas chambers". Nowadays, informed debate is no longer about whether or not there was any German program to exterminate the Jews; it's about whether the false allegations of a 'Nazi' "extermination" program can possibly endure for another year, another three years or another ten years.

Jews' frank admissions about the "Holocaust"

Before going into various proofs of the sheer absurdity and physical impossibility of Jewry's "Holocaust" fable, and evidence of the Hoaxers' deliberate deceptions, let's begin with some candid statements about the "Holocaust" by Jews who chose to speak out after waking up to the reality. An extraordinary letter written by a French Jewish professor in 2004 hits upon a remarkable number of truths.

One Jew to Another
Open Letter To: Mr Simon Wiesenthal
Subject: Nazis Chasing Sixty Years After The War
From: R. D. Polacco de Menasce France 6-27-4

My Dear Sir,

I do think that no Jew will ever dare to tell you the truth.

I am probably the only Jew left who can tell it to you.

I have learnt that you are still chasing very old persons who had responsibilities in the Nazi regime. Sixty years after! People who are eighty-five years old! How shameful!

Do you know one ethnicity who did such a thing in the course of the History of Mankind? You are the very symbol of Talmudic hysterical never-ending hatred.

This is the more egregious as the Nazi regime gave work, sane economy and balance to a whole country, whereas today, everything (when I mention everything, I mean absolutely all) is both Jewish and entirely rotten.

Jewish Capitalism has collapsed the world into all forms of pollutions. Jewish Marxism has slaughtered 200,000,000 people.

To crown it all, everybody knows that there were not 6,000,000 Jews (a country the size of Switzerland) in occupied Europe in 1941 (The American Jewish Year book, mentions 3,300,000 Jews and from that date (1941) on, we all fled to the Free Zone or to Spain towards England). And it is only one million Jews whom Hitler wanted to exchange for trucks at the period of the so-called Shoah. Besides we know that Zyklon B cannot gas 1000 or 2000 people at one time (see M.Roubeix, chief executive of the factory of Saint Avold producing cyanide acid) in gas chambers which have strictly never found norms.

I suppose you would rather have a Jewish USA government enshrined in Jewish finance, pinching petrol in Iraq, spreading Jewish one-worldism, Jewish pornography, 13 Jewish press, Jewish puppets in all governments, than the cleanness of the Nazi regime which made a miracle out of the Jewish rot of the Versailles treaty—the negotiators of which were the Warburg brothers, and that of the Weimar Republic.

You are 95 years of age: if you are not insane what will you tell the Lord when you soon appear in front of Him?

I do wonder.

Entirely disgusted,
R. D. Polacco de Menasce
(Docteur de l'universite de Paris. Thèse de morpho-psycho-endocrinologie—Ret.)

And this is not coming from a so-called "anti-Semite" or "neo-Nazi"; it's from Roger Dommergue (full name Roger Dommergue Polacco de Menasce), a Jewish professor. He can be seen in this video. He also wrote a letter to Steven Spielberg in the 1990s. Here's an excerpt:

The 6-million-gas-chambers myth is an arithmetic and technical nonsense. As a matter of fact the howling, snivelling, Shoah business, 50 years after the war, is disgusting, debasing: it is a disgraceful shame.

No people in History has ever been wailing about its losses 50 years after a war, even its true and real losses. Even if the 6-million-gas-chambers were true, it would be a dishonour to make such din and pump up so much money everywhere: who were the usurers of the Weimar Republic? You know it as well as I do. It is all the more so as we know that 6.000.000 is gross exaggeration and that the Zyclon-B gas chambers are a technical impossibility. (See Degesh Trial in 1949). In fact 150,000 or 200,000 Jews died in the German camps of typhus or starvation. Many others died but as fighters against Germany to which we, the Jews, had declared war in 1933! ( Hitler was allergic to the hegemony of gold and of the dollar: so he could give work to six million unemployed, before the functioning of German armament factories!).

Do you know the book published at this period and written by our congener Kaufmann: GERMANY MUST PERISH? We know that 80,000,000 Goyim were slaughtered in the USSR, in a political regime which was entirely Jewish, from Marx and Warburg, to Kaganovitch, Frenkel, Yagoda, the executioners. We know that after 1945 Americans and Russians killed and raped German communities all over Europe from Lithuania to Albania. We know that 1,500,000 German war prisoners were starved to death after the war (a famous book was published a few years ago, but is ignored to day). You will find here included in French the text of a rabbi: A rabbi pleads guilty: unfortunately I possess neither the German original nor an English translation. You should have it translated.

The Rabbi condemns the Jewish behaviour in Germany 50 years before Nazism and vindicates the emergence of Hitler. As for the harm we have done to Humanity absolutely not redeemed by your excellent films or the virtuosity of Yehudi Menuhin, or the neutron bomb of S.T. Cohen, I wrote a book about it from texts written by important Jews which are much above the most anti-Semitic text written by Goyim. Simone Weil drew a tragic summary:

The Jews, this handful of uprooted people, have been the cause of the uprooting of the whole mankind.

(The Jews refer to the "Holocaust" as the "Shoah", and boast about how "there's no business like Shoah business". The quip originated with former Israeli foreign minister Abba Eban, regarded as being on the "dovish" side of Israeli politics.)

Paul Eisen, another Jew who chose to think for himself rather than swallow unsubstantiated allegations and regurgitate them parrot-fashion, posted "But how could the Holocaust not be true?", in which he offers some ideas on how people came to perceive propaganda as fact. (He also has a longer version, posted in 2005, "The Holocaust Wars".) In another entry on Eisen's blog, he introduces a recent article of the esteemed revisionist Professor Robert Faurisson with some wise comments about the "unravelling" of the "Holocaust" narrative:

More and more people are coming to realise that the previously unassailable Holocaust narrative is in fact, gravely flawed, and among those people are that tight little band of professional Holocaust worshippers - those that make a living (in both money and prestige) out of the Holocaust - and their followers.

These include the Court Historians who routinely prostitute their 'scholarship' for a best-selling book, TV programme or just an old-fashioned bung, those 'Guardians of Truth' who run the various Holocaust institutes such as the Simon Wiesenthal Centre or, here in the UK, the Holocaust Educational Trust, and those High Priests of the Holocaust religion such as the shameless old fraud Elie Wiesel.

Of course, now the whole thing is unravelling, they've got a terrible problem: How to get out of it without appearing to be getting out of it and I've often wondered how they're going to do it. So far they've made quite a few moves in that direction: Lowering the fatality figure on the plaques at Auschwitz, the sign on the Dachau gas-chamber "GAS CHAMBER (BUT NEVER USED)", the abandonment of the search for conclusive evidence and instead bullshitting on and on about 'convergence', and most recently, the move away from the impossible-to-support murder by gas to the (hopefully) more easily supported murder by bullets. It is this that is addressed by this piece by Robert Faurisson

Of course, it won't work because nobody with half a brain believes them anymore. But no matter, as long as they can keep on churning it out, an obsequious non-Jewish world will bend their knees and comply.

So, will one day Robert Faurisson, Germar rudolf, Ernst Zundel, Carlo Mattogno, Jurgen Graaf, David Cole and many, many more receive the apology (and how about some reparations) they deserve?

I'm not holding my breath

David Cole is a Jew, rather ahead of his time, who doubted the Holocaust fable back in the early 1990s. He exposed the fact that one of the alleged "gas chambers" at Auschwitz was actually a former air-raid shelter that had been reconstructed by the Soviets after the war to look like a "gas chamber", to be shown off to gullible tourists. He made a one-hour documentary, in which he tells of how he made a trip to Europe in September 1992 to investigate Auschwitz. The transcript is at this link; here are a few excerpts:

Which brings up another interesting point: what is shown on the tour and what is not. During the tour, you are shown "The Block of Death," the so-called "Wall of Death" -- naturally right next door to "The Block of Death" -- and exhibit after exhibit specifically designed to affirm atrocity stories and to portray Auschwitz as a death machine, the place where internment meant extermination.

But what don't they show you? To start with, a building which could conceivably be called "The Block of Life," a massive disinfestation complex where Zyklon B gas was used daily to combat lice and the disease they carried. These were the real gas chambers except their victims were clothing and mattresses, and their purpose was to preserve the health of the inmates.

Holocaust experts don't deny the purpose of this building; they just don't like mentioning it. After all, why complicate things?

Also forgotten is the Auschwitz camp theatre, the current home of the aforementioned convent of nuns. The last pictures taken inside this building showed pianos and costumes and a stage where the inmates used to put on productions. These days, however, the nuns don't allow pictures to be taken inside.

And finally, we have the Auschwitz swimming pool. Yes, that's right; swimming pool, situated inside the prison compound right along side of the inmates barracks. A beautiful pool with a diving board and 'starters' blocks for races.

To their credit, the Auschwitz camp officials have not tried to remove this distraction. But if you want to see the pool, you need to know already that it exists because you won't find it on the tour.

So basically what we have is a tour that consists mainly of tourists who already believe in the Holocaust story and are perhaps emotionally connected to it in some way, being given a selectively edited tour filled with horror story after horror story and finally ending up at the final stop -- the gas chamber.

[...]

I know from years of my own research and the research of others that proofs of the Holocaust are few. Literally, all there is are the "eyewitness" testimonies and the post-war confessions. There's no picture, plan or wartime document dealing with homicidal gas chambers or a plan to exterminate Jews.

And we can't use the excuse the Nazis destroyed all the evidence because after we had broken the German code, we were able to intercept their secret transmissions including those that came from Auschwitz. The key to understanding the Holocaust story is understanding the true nature of the things passed off as proofs. Everything that is used as evidence of the Holocaust also can be said to have a perfectly normal explanation.

For example, these exhibits are said to be the material proofs of exterminations. There are the piles of human hair. But what does that prove? It is acknowledged that each inmate had his or her head shaved because of the lice problem. That's not denied, so why wouldn't there be piles of human hair?

What about the piles of shoes and clothing. Is that a proof? It's a fact that the prisoners were issued a uniform upon arrival, including shoes. So why wouldn't there be piles of inmates' shoes and clothing? It doesn't prove anybody was killed. And that's giving the Soviets and Poles the benefit of the doubt that the clothes and hair are genuinely from the camp during its operation.

What about the canisters of gas? No one denies that Zyklon B was used to disinfect clothes and also buildings. Zyklon B was one of the premier pest control agents in Europe at that time. It was present in most of the concentration camps including those that were not said to have had homicidal gas chambers in them.

The typhus epidemic that spread throughout Europe during the war and also spread through the camps called for stringent lice control procedures.

Cole asked the tour guide Alicia about the authenticity of the "gas chamber", asking if it was a reconstruction, and she replied that it was in its "original state". He asked if the holes in the ceiling were the original four holes through which the Zyklon B was dropped, and she replied that they were original. And when he asked if any walls had ever been knocked down in the "gas chamber", she denied it. Next, Cole met a tour guides supervisor, and asked about the holes in the ceiling. This time, the supervisor replied that they'd been rebuilt, after the war. Cole managed to arrange an appointment to see Dr. Franciszek Piper, the Head of Archives and Senior Curator. (It was Dr. Piper who was largely responsible for the admission that the claim of "four million" killed at Auschwitz was false, and replaced that with a revised claim of a little over one million - whilst the headline claim of "six million" Jews killed in total remained unchanged - an infamous example of "Jewish mathematics". And as Cole says, "...there is no possibility that even the most extreme Holocaust revisionist in the world could possibly revise the figure any more than the Holocaust 'experts' already have".)

Here's what Piper told Cole:

The first and the oldest gas chamber, which existed in Auschwitz I, this camp where we are now here, operated from autumn 1941 to December 1942, approximately one year. The crematorium near by this gas chamber worked longer, to the middle of 1943.

In July 1943, the crematorium was stopped and the bodies of the prisoners [who] died at Auschwitz I at the time were transferred to Birkenau.

In 1944, in connection with the bombardment of Auschwitz by the Allied forces, [the] empty crematorium number one and gas chamber at Auschwitz were adopted as air [raid] shelters.

At this time, additional walls were built inside the former gas chamber. An additional entrance was made from the east side of the gas chamber and openings in the ceiling, [through which] the gas Zyklon B was discharged [to the] inside, were at the time liquidated.

So after the liberation of the camp, the former gas chamber presented a view of [an] air [raid] shelter. In order to gain an earlier view ...earlier sight...of this object, the inside walls built in 1944 were removed and the openings in the ceiling were made anew.

So now this gas chamber is very similar to this one which existed in 1941-1942, but not all details were made so there is no gas-tight doors, for instance, [and the] additional entrance from the east side rested [remained] as it was made in 1944. Such changes were made after the war in order to gain [the] earlier view of this object.

And Cole goes on to summarize:

Here I think we should recap what Dr. Piper has told us. According to him, the room was a gas chamber but was later turned into an air-raid shelter at which time dividing walls were built, the holes in the ceiling were removed and a new door was added on one side of the gas chamber.

After the camp's liberation, the dividing walls were knocked down, [and] the holes were put in the ceiling. However, the new door was not removed.

[...]

Which brings us to our final point, the reconstruction itself. With the information we now have, we can say there are two different views of the gas chamber reconstruction.

The first one, the official view, holds that the Soviets and Poles created a "gas chamber" in an air-raid shelter that had been a gas chamber. The revisionist view holds that the Soviets and Poles created a "gas chamber" in air-raid shelter that had been -- an air raid shelter. So how do we know which one is correct?

Well, obviously the burden of proof is on those who say that there was a gas chamber at one time in that building. Do they have any evidence at all to support that claim?

In my tenure as a Holocaust revisionist, I'm sure if there was any I'd have seen it. I can also add that those questionable four holes in the roof of the building are not detectable in any of the aerial photograph blow-ups that I've seen.

Cole makes a very important point about the cyanide levels in the delousing chambers versus the alleged extermination "gas chambers":

Another question that should be asked: Is there any Zyklon B gas residue in the gas chamber, knowing that cyanide gas would, in fact, leave a residue?

In 1988, execution equipment expert Fred Leuchter conducted forensic examinations on the gas chambers at Auschwitz to answer that question.

He took samples from the four gas chambers at Birkenau, the one at the main camp and the control sample from one of the disinfestation chambers that we know did use Zyklon B. Now, the gas chamber samples showed almost no appreciable traces whereas the disinfestation sample literally went right off the scale.

More importantly though, in 1990, the Institute of Forensic Research in Krakow decided to conduct their own forensic tests to see if they could refute Fred Leuchter's findings. They did this with Dr. Piper's help.

Their own tests got back the same results so, since then, the question has not been, "Are there any appreciable traces of Zyklon B residue in the gas chambers?" but instead, "Why are there not any appreciable traces?"

Joseph G. Burg (Josef Ginsburg), a Jewish revisionist who was beaten and persecuted by Hoaxers attempting to prop up their 'truth', said, "World War II was a Zionist plot to make way for the foundation of the Jewish State in Palestine." Burg visited Auschwitz in 1945 but found no "gas chambers". He visited Majdanek three times, and found delousing chambers used to liquidate lice and fleas but no homicidal gas chambers. Burg provided much more evidence, too numerous to mention here, refuting the "extermination program" malarkey.

The Toronto Star, March 31, 1988, reported Joseph Burg as saying, "Zionism was willing to sacrifice the whole of European Jewry for a Zionist State. Everything was done to create a state of Israel and that was only possible through a world war. Wall Street and Jewish large bankers aided the war effort on both sides. Zionists are also to blame for provoking the growing hatred for Jews in 1988." Amusingly, the Hoaxer site Nizkor ironically confirmed the quote as genuine after attempting to debunk it by seeking evidence that no Joseph Burg had ever worked for The Toronto Star!!

The plethora of evidence refuting the "Holocaust"

We can start with the forensic evidence that refutes Hoaxers' extermination gas chambers claims, followed by:

the resulting absurdities should the Hoaxer narrative be assumed to be true regardless
Hoaxers' deliberate attempts to deceive with a fraudulent 'study' that was set up to yield the results Hoaxers required
the fact that Hoaxers have no compelling physical evidence whatsoever to back up their allegations (which they certainly would have, had thousands or millions of Jews been "gassed"), and merely have 'documents' of dubious provenance or proven forgery, dubious "eyewitness" testimony that is mostly already confirmed as lies, and 'confessions' extracted under torture and duress
the fact that Hoaxers' duplicity is confirmed from the fact that they have already been forced to retract the vast majority of their claims because they were far too preposterous even for the gullible to believe in, and people were able to see for themselves that the claims were poppycock
the fact that Hoaxers' deception is confirmed by the fabrication of forged 'documents'
the fact that Hoaxers need to prop up their 'truth' by murdering in cold blood, attempting to murder, and repeatedly beating up revisionists, and enacting laws to ban free speech and have revisionists imprisoned and fined for merely stating their views
the fact that camp propaganda (lies) originated with Jewish inmates such as the communist Bruno Baum
the fact that the "six million" figure pre-dates not only WWII but also the death of Queen Victoria
the fact that the same rabbi who was talking about "six million" dead or dying Jews in 1900 said in 1938 that "millions of Jews are dying today" and led an organization that was peddling early WWII extermination stories from May to August of 1942, in which Jews were allegedly being exterminated by "firing squad" in a "vast slaughterhouse" - amusingly, they knew exactly how many but couldn't say where the alleged "slaughterhouse" was (since they knew that would have enabled the Germans to refute the claim), and the mass murder by "firing squad" allegation was quietly abandoned
the fact that the extermination chambers narrative is a physical impossibility given the known laws of physics and mathematics.

And last, but not least, we can fit in somewhere below how Hoaxers' deception is confirmed by a patently fraudulent TV "documentary" posing as 'fact', in which a dig at a Polish cemetery is passed off as 'evidence' of "mass graves" at Treblinka, and a pierced mullet star - a brand mark of a 125-year old Polish porcelain factory - is passed off as a "Star of David" and proudly proclaimed as 'evidence' of "gas chambers". These Hoaxers have even plagiarised revisionist Richard Krege's methodology (albeit for a sound bite, not for practising it) by claiming to have conducted a "study" using "ground-penetrating radar", after Krege and an Australian team had already conducted a real study using ground-penetrating radar at Treblinka in 1999 and found zero evidence of mass graves. (It might seem hard to believe that Hoaxers truly are this desperate. But they really are; this is a seventy-year-old hoax - the Hoax of the 20^th century - in its death throes, after decades of unravelling. It's history in the making!!!)

The forensic evidence against homicidal gas chambers

The chemist Germar Rudolf conducted his own independent forensic tests at Auschwitz in 1992, which confirmed the findings of Leuchter (1988) and of the Jan Sehn Institute for Forensic Research (IFR) of Krakow (1990/1). Rudolf's report was published in German in 1993, after Cole made his documentary. Leuchter wrote four reports in total over 1988-1991, which all showed the "gas chambers" allegation was a myth. The forensics confirmed large scale use of cyanide in delousing chambers, but zero or trace levels in the alleged "gas chambers". There was a fraudulent, pseudo-scientific 'study' commissioned by the Polish government and conducted by IFR in 1994, which gave conflicting results. That came after IFR's first study had failed to give Hoaxers the 'right' conclusion. This demonstrates how the Hoaxers, lacking any credible evidence or argument whatsoever, are compelled to resort to deliberate deception. More on that below.

(The IFR never officially released their 1990 study; the article was smuggled out by persons unknown in 1991.)

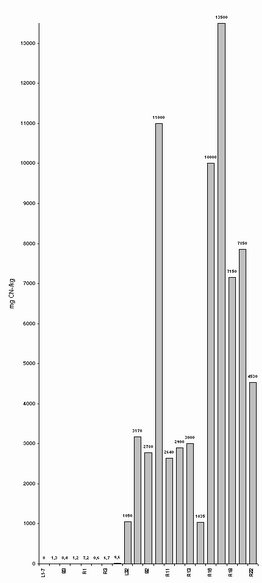
DelousingVsGasChambers photo DelousingVsGasChambers_zps93bef073.png

Source: Dissecting the Holocaust [5.3.2, Graph 2], Germar Rudolf

The trace levels of cyanide on the left of the graph are those of the alleged "gas chambers", and the high levels of cyanide on the right are those for the delousing chambers. See the source for zoomable image and also Table 3, too large to add here, but which shows how cyanide levels in the walls of the alleged "gas chambers" exhibited zero or trace levels of up to 7.9mg/kg, compared to a cyanide content of walls of the delousing chambers ranging from 1,035 to 13,500 mg/kg. Thus, with "gas chambers" in the mg/kg region whilst delousing chambers were in the g/kg region, the delousing chambers that were used to save prisoners' lives by killing billions of typhus lice had around 1,000 times the cyanide levels of the so-called "gas chambers" that were allegedly used to exterminate prisoners. In any case, the levels in the "gas chambers" were regarded as too low to be reliably interpreted as indicating anything other than a building selected at random.

After Leuchter's first study, the historian David Irving said, "The Jewish community have to examine their consciences. They have been propagating something that isn't true." That's an exceedingly polite way of describing it!

Hoaxers accepted the massive difference in cyanide levels, and attempted to 'explain' it by suggesting that killing lice is very hard, but killing humans is very easy and required only a minimal quantity of cyanide. In this scenario then, the Germans are fighting for their very survival on all fronts against the US, the Russians, the French, the British, etc., and they inexplicably allocate scarce resources to an "extermination" program to kill six million Jews for which there is no budget, and no written orders. Moreover, this massive "extermination" program is carried out not in Germany, but in an occupied territory. Inexplicably, they chose to devote scarce resources to shipping millions of Jews to occupied nations (Poland, USSR/Ukraine, etc.) in order to gas them, rather than simply shooting them in Germany. And to cap it all, they bizarrely allocate 99.9% of their Zyklon B to saving their prisoners' lives, and the other 0.1% to killing them!

Had the Germans really been as dim-witted as that, they would not have held out for six years. The war would have been over within six weeks, if not six days.

The bizarre strategy of preservation-extermination wastes scarce resources by requiring tons of Zyklon B, whereas a simple extermination would require merely kilos. Or better yet, the prisoners would simply be shut in airtight chambers to asphyxiate, with the advantage that there would be no need to wait for the poisonous gas to disperse. Any victims who remained alive could be moved to the front of the queue for the ovens, and if necessary, knocked unconscious first. Preservation-extermination is like someone who goes out into their garden when it's raining, puts up an umbrella to keep themselves dry, and then turns on a hose to get themselves wet.

The Hoaxers' scenario is comparable to the US deciding to invade and conquer the world, beginning by invading Canada and choosing to indulge in exterminating the Jews. But rather than summarily despatch Jews where they stand with bayonets or a bullet to the back of the head, they are transported to occupied Canada, whereupon "death camps" are constructed, and massive resources are devoted to preserving the lives of the prisoners. There are no written orders for the "extermination" campaign, and no budget for it. The camps are also equipped with a hospital, theater, library, swimming pool, several orchestras, etc. And at the same time, the same medicines that are used to preserve prisoners' lives are also used, at a thousandth of the cost, to poison them to death!

In the twisted, perverted, paranoid, delusional 'reality' of the Hoaxers, absurdities are perceived as normal, and gigantic conspiracies are imagined where none existed.

David Cole told of how Piper attempted to 'explain' the lack of appreciable traces of any cyanide residue in the "homicidal chambers" by claiming they were used "about 20, 30 minutes during 24 hours" whereas the delousing chambers were used "day and night". Cole points out that this not only contradicts "eyewitness" testimonies of "repeated homicidal gassings going on day and night", but contradicted Piper's own claims when he later told of multiple gassings each day.

Another Hoaxer tactic is to claim that because the Germans (supposedly, and how conveniently!!) destroyed "evidence" by dynamiting the "gas chambers", the "gas chambers" cyanide was exposed to the elements, and so did not survive. The Nizkor site at the above link, for example, where they attempt the "killing lice is very hard" gambit, claims: "Furthermore, the delousing chambers are intact while the extermination chambers were blown up (a .GIF picture of the one of Krema II is available). Therefore, their walls have been exposed to the elements for the last 50 years. The ruins of the gas chamber of Krema II are covered with about 3 feet of water during certain periods of the year; HCN compounds easily dissolve in these surroundings." (In reality, of course, the only people who destroyed - or created - evidence were the Soviets; the Germans had no motive to do so.)

The lie that cyanide compounds were not detected because they were exposed to the elements was also plugged by Hoaxer "Professor" Robert Jan Van Pelt. Needless to say, the claim has been thoroughly debunked by Rudolf: "The relevant literature consistently describes Iron Blue as an extremely stable pigment. It is insoluble in water, resistant to acid rain and also surprisingly resistant to sunlight. When exposed to weathering, other compounds of hydrocyanic acid will even convert preferentially into Iron Blue."

Rudolf gives several examples, one of which is the fact that the Iron Blue on the exterior southwest wall of the delousing wing of BW 5b in the Birkenau camp was still highly visible after 50 years of weathering, when the below photo was taken. Also see Dissecting the Holocaust, Some Considerations about the 'Gas Chambers' of Auschwitz, 3.3.2 or The Rudolf Report 6.6. The solubility of Iron Blue, for example, is 10^-27 g of Iron Blue per g of water.

This leads to some fun calculations. Suppose you wanted to dissolve a mere one gram of the Iron Blue in the picture below. (At around 10,000 mg/kg, the cyanide alone is some 1% of the mass of building materials, within samples taken. There is a lot more than one gram of Iron Blue there.) The mass of water required is 10²⁴ kg; a little over one-sixth the entire mass of the earth. The total mass of earth's oceans is reckoned at 1.35 x 10²¹ kg (about 1/4,424 the mass of the earth). Thus, all of the water in the oceans would need to converge upon that wall, 741 times over in 50 years, or once every 25 days. And even then, a large multiple of that would be needed to remove not just 1 g, but all of the Iron Blue to get down to the trace levels of the "gas chambers". And that applies for each wall of the so-called "gas chambers". And even then, the Hoaxers haven't explained the 'coincidence' of why those impossible events happened only with "gas chambers" and not with delousing chambers' exterior walls, which is not surprising, given that they would need to postulate an "anti-Semitic", supernatural "Being" to selectively orchestrate those supernatural phenomena.

So much for Hoaxers' claims that the compounds would "easily dissolve"!

CyanideExteriorDelousing photo CyanideExteriorDelousing_zps0e342724.png

Source: The Rudolf Report [8.3.3.3, Fig. 71], Germar Rudolf

(Also see Fig. 68.)

Hoaxers' deliberate attempt to deceive by fixing their 'study' to give them the 'right' result

After the four Leuchter reports, the Rudolf report, and the leaking of their own IFR report of 1990 that ironically also confirmed the revisionist position, Hoaxers were in an even bigger hole than usual. So in 1994 they had Markiewicz et al at the Krakow Institute for Forensic Research conduct a 'study' that would come up with the 'right' results. They needed some way of obtaining similar cyanide levels in delousing chambers and mortuaries ("homicidal gas chambers"). By using a fraudulent methodology in which they would only look for unstable cyanide salts, and certainly exclude the stable Iron Blue, their study would reveal only trace amounts of cyanide in both delousing chambers and "gas chambers". And in order to justify using such a deliberately fraudulent methodology, they pretended that "It is hard to imagine the chemical reactions and physicochemical processes that could have led to the formation of Prussian blue in that place." In contrast to their 1990 study that was never officially published because it had failed to give Hoaxer-friendly results, they did publish the 1994 study.

Germar Rudolf addresses the fraudulent IFR 'study', for example, here, and in Dissecting the Holocaust, Some Considerations about the 'Gas Chambers' of Auschwitz, 5.4 [pp. 369-371].

One thing to note is that Markiewicz and his gang at the IFR had already been attempting to fix the results in their 1990 study, by not looking for Iron Blue. However, despite their manipulations, they'd failed to get their politically desired results. All but one of their "gas chambers" samples had failed to show any cyanide, and they still got twenty times higher cyanide levels in delousing chambers than in the "gas chamber". So rather than publish the 1990 study, they chose to keep on tampering until they got the 'right' results. However, the 1990 study was leaked in 1991 and serves to corroborate Leuchter - even though the results were already biased in favor of Hoaxers.

In their 1994 study they tampered with their methodology even further, focusing on unstable cyanide compounds. By this point of course, they're so far from seeking what they should be looking for, that they find less than one part per million parts of building material (compared to Leuchter / Rudolf's more than one part per thousand); it's almost as if they were looking for gold. And even then, the delousing chambers had more cyanide than the "gas chambers".

PolishIFRFraud photo PolishIFRFraud_zpseb7581a4.png

Source: Germar Rudolf

The absurdity of the Hoaxers' allegations

Even after all that deliberate deception on the part of the Hoaxers, and supposing it had worked a little better than it had, we would still have the bizarre scenario of the Germans allocating 50% of their Zyklon B to saving their prisoners' lives and the remaining 50% to killing them, and the absurdity of the work camp with a swimming pool, a brothel, a library, several orchestras, a theater, a museum where their artwork was displayed and a hospital, that also doubled up as a "death camp", and the requirement that the laws of physics and mathematics were suspended whenever the crematoria or the gas chambers were operating. Thus, one breed of Hoaxer peddles the above scenario which relies upon a pseudo-scientific tampering with the results of forensics and yet is still crackers; another breed of Hoaxer claims the Germans used 99.9% of their Zyklon B to save their prisoners' lives and the other 0.1% for killing them. Both are believable only by those who are a few sandwiches short of a picnic, by those who simply don't bother to think critically about their own beliefs, by those who exhibit little interest in the world around them, and by those who are afraid of the truth.

In case Hoaxers should attempt an 'explanation' along the lines of "First they were trying to save the prisoners, then they decided to exterminate them; thus, they were not saving them and killing them at the same time and there is no resulting absurdity" (with, of course, no evidence for that allegation), the scenario is refuted by the deliveries of Zyklon B to Auschwitz. In 1942 Tesch delivered 7.5 tons; in 1943, 12 tons; and in 1944, 6 tons. If we accept the Hoaxers' contention that the 1,000-fold difference in cyanide levels is a consequence of a thousand times as much HCN being needed to kill lice as opposed to humans, it follows that if an extermination program was suddenly introduced and the labor camp turned into a "death camp", Zyklon B usage would be expected to decrease 1,000-fold at that time. Alternatively, Hoaxers might try suggesting that an extermination program was not introduced until halfway through 1944, which would account for the reduction to 6 tons in 1944. In this case the Germans would have to gas and cremate 1.1 million or 1.5 million within six months, before Auschwitz fell into Soviet hands in January 1945. That's 6,023 (or more) per day, 251 every hour, if the gas chambers and ovens were running 24/7. They must also ignore contradictory Hoaxer claims (e.g., Franciszek Piper) that the lack of cyanide residue in the "gas chambers" is explained by operation for only 20 or 30 minutes a day. Or they could claim that the gas chambers could process at a rate of 6,023 in less than half an hour. Someone would probably believe it!

In July 1990, shortly after Leuchter's report was published, Hoaxers were forced to drop their claim of "four million killed at Auschwitz" in an attempt to salvage their last remaining vestiges of credibility. Hoaxer estimates for the Auschwitz death toll vary from half a million to nine million, but most widely quoted today is 1.1 to 1.5 million. In 1992, Franciszek Piper was claiming both 1.1 million and 1.3 million. Jews tried to spin the 1990 revision by blaming the Poles, accusing them of exaggerating the number of non-Jews. This particular Hoaxer fantasy supposes that Jews always believed there were a little over a million Jews killed at Auschwitz, and for more than four decades, officials lied and pretended that nearly three million extra non-Jews had died there. In this way, Jewish fraudsters hoped to get away without a downward revision of their "six million Jews" headline figure, and to still come out of the fiasco smelling of roses. Even if a million Jews were killed at Auschwitz - which they weren't, Jewish Hoaxers have yet to explain how and where the remaining five million were supposedly murdered, and provide evidence. (After seventy years!!!) They now allege 1.5 million Jews were killed in the Ukraine, and say that the executions became, "in a sense, invisible." Yes, exactly like Santa Claus and the tooth fairy!

The idea that Jews always thought only around a million Jews died in Auschwitz-Birkenau, and would never have stooped to exaggerating the figures, is belied by the Jewish Virtual Library's allegation that "Historians and analysts estimate the number of people murdered at Auschwitz somewhere between 2.1 million to 4 million, of whom the vast majority were Jews." And by JewishGen.org, which claims for Auschwitz-Birkenau: "2.1 to 2.5 million killed in gas chambers, of whom about 2 million were Jews".

Amusingly, another Hoaxer tactic is to blame the Germans for not keeping good records. David Cole said in 1992, after the major revision in the death toll, "We are told in the Auschwitz guidebook and also by other sources that the reason it was so difficult to ascertain the number of victims at Auschwitz was because the Nazis had destroyed the appropriate records. This concept was also repeated to me by Dr. Piper." And as late as June 2013, Israel's national "Holocaust" museum Yad Vashem claimed "...the Nazis did not keep meticulous records." But in 2007, The New York Times stated that "The Nazis, of course, kept meticulous records of their mass extermination during World War II...".

The true death toll at Auschwitz-Birkenau

The Soviets found those records at the end of the war, and locked them away in a secret archive. By 1990, the Russians agreed to hand the death books over to the Tracing Center of the International Red Cross in Bad Arolsen, Germany. As of the end of 1943 (see Rudolf, Lectures on the Holocaust, p.262, [.pdf download]), the death books recorded 68,751 deaths of registered prisoners at Auschwitz. [June 2015 update: See this page for a detailed breakdown; the total for July 1941 to December 1943 show 68,864 dead, including 29,125 Jews and 31,814 Roman Catholics.] The Auschwitz-Birkenau Memorial and Museum says the "almost 69,000" deaths are of registered prisoners "who died between July 29, 1941 and December 31, 1943". This would suggest a total figure including 1944 of around 100,000, including about 40,000 to 50,000 Jews. That level of casualties would be consistent with the capacity of the crematoria (as will be demonstrated below), and consistent with a reasonable expectation of the number who died from typhus, other natural causes, and the breakdown in the supply of food and medicines following intensive Allied bombing of supply lines at the end of the war. And it is consistent with the proven fact that there were no homicidal gas chambers, and there was no extermination program!

(In 1993, Carlo Mattogno estimated 160,000 to 170,000 deceased registered inmates at Auschwitz and Birkenau, based on an assumption of additional deceased female inmates being recorded separately in undiscovered registers. 170,000 is at the upper limit of the crematoria capacity, based on available fuel and the lifespan of the firebricks. 170,000 is a possible figure, at a stretch, whereas 1 million and 4 million are in the realm of fantasy.)

The extrapolated estimate for total Jewish deaths at Auschwitz-Birkenau above, is based on the admission of the Auschwitz-Birkenau Memorial and Museum that there were more Roman Catholics than "Mosaics" (Jews) registered in the Death Books:

"An analysis of the 'denomination' item shows that the majority of the registered prisoners in the Death Books were Roman Catholic (31814 persons - 46,8%) and Jewish ('Mosaic') (29125 persons - 42,8%). Others belonged to the following denominations: Greek Orthodox (3,6%), Evangelical-Lutheran (3,4%), and Greek Catholic (1,6%). This item is left blank on 1,275 (1,9%) death certificates."

That range of tens of thousands up to possibly 100,000 Jews, which is an order of magnitude below Hoaxers' allegations, is corroborated by evidence below.

Hoaxers' contempt for free speech

Even if we accept the lower, revised estimates of 'only' 18,000 to 25,000 inhabitants of Dresden murdered by Allied firebombing in 1945, it's still around half the total number of Jews who died at Auschwitz. However, in contrast to Dresden, whilst a few Jews may have been shot or hanged for spurious reasons, the vast majority did not die as a result of the malice of their enemies, but from natural causes, later exacerbated by the malice and negligence of their supposed 'allies', i.e., Allied intensive bombing of the food / medicines supply chain towards the end of the war. And the fact that hundreds of thousands were originally believed to have died at Dresden demonstrates how Allied governments had a powerful motive to collude with Jewish Hoaxers. Both had an interest in portraying the Germans as evil monsters - Zionist Jews in order to grab Palestine, and Allied governments in order to justify, and distract from, their own war crimes. Once the web of lies had been spun, they had to keep trying to stop it unravelling, whether by blowing up François Duprat's car killing him and disabling his wife, kicking in Dr. Robert Faurisson's face, or jailing other revisionists, even David Irving who, in the interests of accuracy, accepted responsibility for inflated figures for Dresden, which is hardly the act of a right-wing "extremist". Decades later, Jews still need their "Shoah" in order to justify their fraudulent annexing of Palestine and continuing receipt of more than $70 billion in "reparations" to date, and governments continue to prop up the lies of previous administrations since they fear being removed in a bloody revolution.

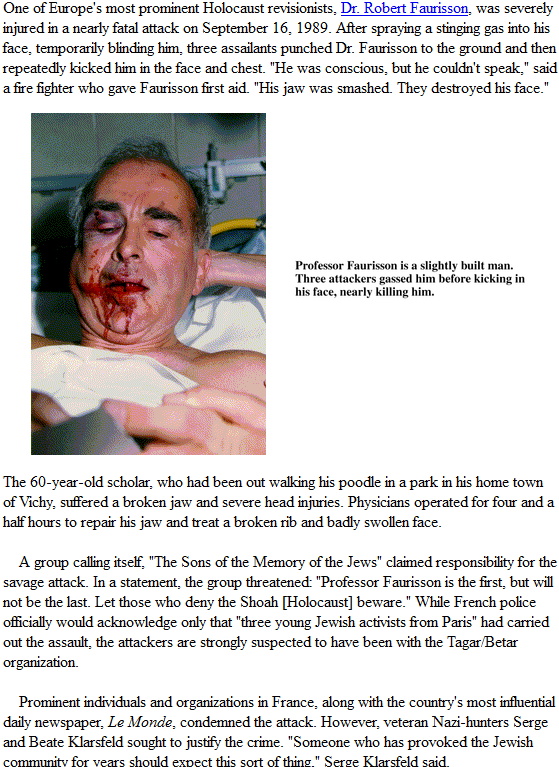
FaurissonAttacked photo FaurissonAttacked_zpse2fa593d.png

Source: Thought Crimes Archive

Any 'truth' that can only be sustained by the use of bombs, acid, boots, fists, arson, imprisonment, fines, etc., is not a truth; it's a religion. And there has never been any other group still whining about their supposed "losses" and continuing to collect massive reparations, 70 years after the alleged "crime" is supposed to have been committed.

Hoaxers' preposterous conspiracy theory

Hoaxers try to have it both ways, by pretending that the Germans kept meticulous records for all the Auschwitz-Birkenau inmates who'd been "innocently" dealt with - i.e., they were put to work for Germany's war effort, and either survived or died of natural causes, and then there was another group of "secret" inmates who'd been exterminated, and the Germans had stealthily managed to leave no traces of these, so that the executions became, in a sense, invisible - just like Santa Claus and the tooth fairy. And somehow, it's simply another big "coincidence" that the number of registered deaths according to the Germans' meticulous records just happens to coincide with the number of people who could be cremated given the available fuel, available time, and capacity of the crematoria. And the Germans had found a way of circumventing the laws of thermodynamics and mathematics so that they could "exterminate" all those extra people who'd been craftily omitted from the records in order to cover up the evidence, for a secret extermination program for which there was no written orders, no budget, no German photographs or film footage, no Allied overhead photographs, no mention of "gas chambers" in Eisenhower's or Churchill's war memoirs, no autopsies, no forensics, no pedal-operated brain-bashing machines, no electric plates, no quicklime trains, no holes in the ceiling, no homicidal gas chambers, no murder weapon, and no evidence apart from highly dubious 'eyewitness testimony', forced 'confessions' and forged 'documents'. William of Ockham would be turning in his grave.

In any case, the idea that those unfit to work were simply gassed upon arrival, and kept off the books to conceal the crime, is refuted by an examination of the ages of the 68,751 registered prisoners who died at Auschwitz up to the end of 1943. If inmates had been selected out for murder below or above specific ages, the age distribution curve would be expected to fall sharply at the specific ages. Instead, the curve is more bell-shaped, with 2,584 (3.7%) below the age of ten, and 2,640 (3.8%) above the age of 60. There were 75 deceased of age 80 or older. Are we really supposed to believe that the Germans were cunning enough, not only to leave "gassed" prisoners off the books, but also to fake fictitious very young and very old prisoners, in order to cover up evidence of an invisible extermination program? And at the same time, the Germans are supposed to be too moronic to realize that it didn't make sense to allocate 99.9% of their Zyklon B towards saving their prisoners' lives whilst they were using the other 0.1% to murder them!

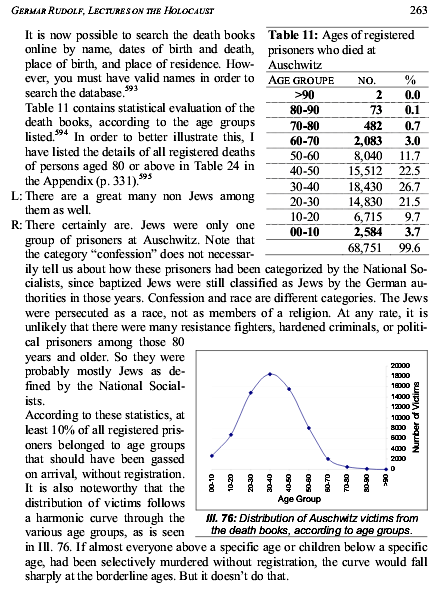
DeathBooksBellCurve photo DeathBooksBellCurve_zps0c894cbb.png

Source: Lectures on the Holocaust [p. 263], Germar Rudolf, .pdf download

There is also the fact that Anne Frank, b. June 12, 1929, arrived at Auschwitz at the age of 15 in 1944, and survived in that alleged "factory of death", only to die of typhus at Bergen-Belsen, which even Hoaxers nowadays concede was not a "death camp" (one Hoaxer claimed to have survived "gas chambers" there not once, not twice, but six times!!!!!!). One part of the Anne Frank legend, which holds that she narrowly escaped being gassed on arrival at Auschwitz in 1944 because she was three months over the age of 15, is refuted by the death books showing 2,584 registered deaths under the age of ten. Moreover, Hoaxers admit that Frank was moved from Auschwitz to Bergen-Belsen because she had scabies. A "factory of death" dedicated to the mass murder of Jews, and, rather than gas a 15-year-old Jewish girl with scabies, the Germans allocate scarce resources to transport her to another camp???

The Hoaxers are in a most unenviable position. The only 'evidence' they have consists of confessions obtained under torture and duress, 'documents' - which can be forged or misrepresented, and the few remaining "eyewitness" testimonies yet to be directly refuted. Those testimonies can already be indirectly refuted in that it can be induced that they are lying because most of the "eyewitnesses" have already been exposed as liars and none have been confirmed as honest, and it may be deduced that they are lying from the simple fact that the "gas chambers" and crematoria could not possibly operate as claimed under the known laws of physics and mathematics, and forensic evidence has already refuted the claim of homicidal gas chambers. All of their physical 'evidence' has a perfectly innocent explanation, they have already been forced to retract most of their allegations (that were supposedly from "eyewitness" testimony, thereby confirming the "eyewitnesses" as liars!), and their arguments are riddled with contradictions, absurdities and physical impossibilities.

For example, as seen with Auschwitz's Dr. Piper, when faced with the problem of massive amounts of cyanide residue in the delousing chambers but none in the so-called "gas chambers", one Hoaxer tactic is to claim the "gas chambers" only operated for 20 or 30 minutes a day. However, even if they were operating for 24 hours a day, that would still be insufficient to account for all of the alleged victims as will be demonstrated below, and so when someone asks about the number of victims, Hoaxers change their story so that the "gas chambers" were operating most or all of the day, as the liars attempt to reduce the overwhelming gulf between claim and reality.

Hoaxers' forging of "documents"

Ingrid Weckert demonstrated that the Nuremberg document PS-501 was a forgery. The 'document', supposedly written by SS-Untersturmführer Dr. August Becker, purportedly 'proved' the existence of homicidal "gas vans" or "death vans" - "gas chambers" on wheels. In Dissecting the Holocaust, the chapter "The Gas Vans: A Critical Assessment of the Evidence", after setting out the evidence, Weckert concludes:

"We have found that the origin of the letter from Becker to Rauff which was submitted to the Nuremberg Tribunal as Prosecution Document PS-501 is uncertain, and hence dubious.

The handwritten notes on the first page of the letter appear to be nonsensical and certainly were not written by the persons (Rauff and Pradel) whom the initials 'R' and 'P' are supposed to suggest. This would indicate a forgery.

The carbon copy bears the same notes at precisely the same places as the original letter. This is not only unusual, but also an impossible feat of handwriting. At least on the carbon copy, the notes can only have been added photo-mechanically. This too would indicate a forgery.

The contents of the letter are not credible, especially in their nature as letter from a subordinate to his superior.

All in all, these points are cause for grave doubts as to the authenticity of the document."

A Hoaxer made a pathetic, half-hearted attempt to counter Weckert's refutation of the PS-501 'document', which fails to address her main arguments and the points raised in her evidence, cites other 'documents' also of dubious origin that are supposed to back up the first forgery, and fails to prove the authenticity of any of the 'documents'. The "gas vans" allegations were also debunked by Jürgen Graf.

John C. Ball's 117-page report on air photo 'evidence' is now available online in its entirety, and shows how marks were added to photographs by CIA operatives, sometime after 1944. The CIA didn't even release the photos until 1979. In those days, tampering had to be painstakingly carried out by hand. After 9/11, it only took forgers 34 months to fabricate a grainy "surveillance video" lacking time and date stamps, purporting to show "hijackers" at one of the airports (the Flight 11, 175 and 93 "hijackers" allegedly managed to board their final flights without being caught on camera - before about half of them turned up alive and well!).

After the Simon Wiesenthal Center was caught forging a photograph of Auschwitz by adding fake "smoke", they tried to 'explain' it by claiming it was a "smudge on the photo" and they'd "incorrectly identified [it] as smoke from the chimneys." A "smudge" that 'coincidentally' happened to be in the right place, so as to appear like smoke from the chimneys? Even mainstream sources recognize that Simon Wiesenthal was a "liar and a fraud", who lied about nearly everything in his life. He had numerous contradictory versions of his wartime exploits, which in any case were so far fetched that they are virtually a benchmark test of gullibility.

Hoaxers' rapid abandonment of most of their allegations

Most of the Hoaxers' early claims fell apart, because people were quickly able to see that there was no substance to them. It was wartime propaganda gone mad. Hoaxers quietly abandoned their claims of Jews being made into soap, knife cases, light switches, lampshades, saddles, riding breeches, gloves, house slippers, ladies' handbags, and book-binders, along with death by steam, electrocution, pedal-operated skull-smashing machines, tree-felling, vacuum chambers, chlorine gas, drowning, bathing in cold water, being thrown into a quarry, being torn apart by a bear and pecked by an eagle, and so on. For example, Hoaxer Jan Karski claimed to have witnessed Jews being killed by "quicklime". But even Hoaxers had to concede that Karski's "eyewitness" testimony was a pack of lies, and needless to say, it's been thoroughly debunked.

One of the Hoaxers, who isn't even Jewish, was ordered to pay back $22 million to her publisher after her lies were exposed. "Misha Defonseca", whose real name is Monica Ernestine Josephine De Wael, claimed to have been adopted and looked after by a family of wolves as a young Jewish girl fleeing the Nazis, but actually spent the war as a student at a Belgian school.

There was even a bizarre allegation that Germans had murdered 20,000 Jews near Auschwitz in an "experiment" with an "atomic" device. Nuremberg trial judge Mr. "Justice" Jackson, cross-examining Albert Speer, asked, "And certain experiments were also conducted and certain researches conducted in atomic energy, were they not?" Speer replied that the Germans were a year or two away from splitting the atom, and Jackson asked, "Now, I have certain information, which was placed in my hands, of an experiment which was carried out near Auschwitz and I would like to ask you if you heard about it or knew about it. The purpose of the experiment was to find a quick and complete way of destroying people without the delay and trouble of shooting and gassing and burning, as it had been carried out, and this is the experiment, as I am advised. A village, a small village was provisionally erected, with temporary structures, and in it approximately 20,000 Jews were put. By means of this newly invented weapon of destruction, these 20,000 people were eradicated almost instantaneously, and in such a way that there was no trace left of them; that it developed, the explosive developed, temperatures of from 400° to 500° centigrade and destroyed them without leaving any trace at all. Do you know about that experiment?"

Speer, like any rational person, replied, "No, and I consider it utterly improbable...". Jackson asked, "The reports, then, of a new and secret weapon were exaggerated for the purpose of keeping the German people in the war?" Speer replied, "That was the case mostly during the last phase of the war...".

What seems to have happened here is that Hoaxers - probably Soviet black propagandists - fabricated a 'document' with "information" purporting to show that Germans killed 20,000 Jews with an atomic bomb. The claim was concocted prior to the Hiroshima / Nagasaki bombings of August 6 and 9, 1945, yet the Speer questioning came afterwards, on June 21, 1946. By then, the effects of atomic explosions were well known, and Jackson was aware that the claim was probably too absurd to be sustainable, even in the make-believe atmosphere of the farcical Nuremberg trials. But he still thought it was worth bringing up on the off-chance that Speer might have confessed or revealed some useful information.

After the case was cited by pro-revisionist, pro-truth websites as an example of Hoaxers' preposterous allegations, the deceptive Hoaxer site Nizkor had the audacity to accuse revisionists of "deceit and misrepresentation"!!! Nizkor spun it by suggesting the "death by atomic bomb" allegation somehow didn't count because Jackson knew it was false all along and Speer didn't accept it. The discredited Nizkor writer Jamie McCarthy has to avoid the fact that Jackson's 'document' with the "information" was obviously created by Allied, not Axis, propagandists, to promote the "Holocaust" hoax, and at the time it was fabricated, they clearly hoped that the charge would fool some people and help to vilify the Germans, or they wouldn't have bothered to concoct it. McCarthy and other internet shills needed to sell the idea that the Germans had circulated the claim of 20,000 dead Jews to boost morale as Germany was losing the war, yet any open admission of an extermination program by German leaders would contradict Hoaxers' allegations of a secret conspiracy to mass murder millions of Jews, in which the Germans supposedly took great pains to avoid leaving any evidence, even to the extent of dynamiting "gas chambers", using coded terms such as "special treatment" at all times, having no written orders or budget for an extermination program, and digging up and cremating nearly a million corpses at Treblinka. If there ever was a 'document' of German origin that provided evidence of 20,000 Jews murdered by an atom bomb, you can be sure that Hoaxers would be milking it for all it was worth.

The absurd allegations of a death camp at Treblinka, and Hoaxers' desperate attempts to prop up the legend

Hoaxer yarns about mass murder by "vacuum chambers" or "steam chambers" at Treblinka were crazy enough, but when they abandoned that and tried the "gas chambers" gambit instead (Diesel exhaust from captured Russian submarines or Soviet tanks), the claims were just as patently ridiculous. Hoaxers needed to claim a large number of deaths to get to their headline total of "six million" (already decided upon before the 20^th century), and so they chose to claim up to a million (870,000 was frequently cited, and now they allege 700,000 to 900,000) dead for Treblinka. Problem was, the Hoaxers didn't have a shred of evidence because their story was a total pack of lies. So they allege the 'Nazis' murdered about 800,000 Jews at Treblinka, buried them all in mass graves, panicked and decided to get rid of the evidence, dug up the 800,000, and cremated the 800,000 together with the latest "gassing victims". This, they reasoned incorrectly, would 'explain' why there were no mass graves. (It's hard to believe that even Hoaxers have the audacity to persist to this day with such risible nonsense, but they really do!!!)

The part about cremating 800,000 bodies is particularly difficult for Hoaxers. Treblinka didn't have any crematoria, and so they had to use wood for fuel. To make matters even worse for Hoaxers, the eastern "extermination" camps used green wood not seasoned (dry) wood. Jürgen Graf says that Carlo Mattogno's original calculations in the Graf / Mattogno book about Treblinka stated that 160 kg of wood is needed to cremate a human body, but that's assuming dry wood. In the case of green wood, 300 kg per body is required. (The conversion factor for green tons to dry tons is about 0.5; 0.463 for softwood and 0.529 for hardwood.) Czech Jew Richard Glazar, a witness, said there were 25 woodcutters, and so the Germans were supposedly using freshly cut green wood from the nearby forest, rather than having wood brought by rail or truck. The witnesses said the cremations were carried out between March and September of 1943, so lasted no longer than 7 months. Thus, the amount of wood required is 800,000 * 0.3 = 240,000 tonnes of fresh wood. Each woodcutter has to cut 9,600 tonnes, 1,371 tonnes per month, or 45 tonnes per day.

So what productivity do woodcutters achieve in reality? Graf cites an internet source in which six Italian woodcutters were able to cut and saw 50 tons of wood in 15 working days, working from sunrise to sunset, which is 0.555 tons per day per woodcutter. (The source also points out that they were twenty-year-olds with "muscles of steel", were fed on bread and cheese, sausages, eggs and bacon, and had good quality, sharp hatchets and a variety of saws.) Thus, the 25 Jewish woodcutters, subsisting on the Treblinka camp rations, and using the same tools but needing to have them sharpened or replaced quite a few times along the way to cutting 240,000 tonnes, supposedly achieved 81 times the productivity of their Italian counterparts and maintained it for seven unrelenting months. More realistically, let's suppose the Jewish woodcutters were able to achieve the same productivity as the sausages-eating, bacon-eating Italians, in which case it would take them 240,000 / (25 * 0.555) = 17,297 days = 47.3 years = until July 1990.

There was no massive area of deforestation at Treblinka, and no aerial photos of mass open-air cremations. The Treblinka narrative is also blown apart by the fact that there is no evidence of mass soil disturbances, whereas such evidence would be an inevitable result of the burial and exhumation of 800,000 bodies. Forensic studies are naturally anathema to Hoaxers, since they are well aware that they can only get the 'right' result by cheating and tampering with the methodology, as in the case of Markiewicz and the Krakow Institute for "Forensic Research". In 1999, the revisionist Richard Krege conducted a study at the territory of the former Treblinka camp using ground-penetrating radar. There should have been an area of around a million square feet of soil disturbance. However, the study found "Almost all of the ground consists of undisturbed soil, sand and rocks. The trees are over 50 years old." And what it didn't find was "Individual or mass graves, fragments of skeletons, human ashes, wood ashes, ground irregularities, construction compounds or remnants, remains of trees or stumps, cavities, [or] golden teeth."

More recently, in January 2012, the Hoaxer Dr. Caroline Sturdy Colls claimed to have uncovered "evidence" of mass graves and "gas chambers" at Treblinka using ground-penetrating radar. Announcing that "evidence" has been found makes for good TV and news stories, but Colls' 'research' was soon exposed as yet another Hoaxer fraud. Colls claimed to have found four pieces of ceramic tile with "Stars of David" on them, which supposedly 'proved' that they were on the site of the alleged "gas chambers". But the symbol was on the back of the tile, where it would have been cemented to the floor, not visible, and thereby making "Colls's claim that the symbol was there to 'make people think they were going somewhere safe' complete nonsense". More importantly, the New Observer debunking goes on to say: "But, even worse for Colls, Schute, and the Smithsonian, the symbol which they all claim to be a 'Star of David' is nothing of the sort. It is in fact a brand mark of the 125-year old Dziewulski i Lange porcelain factory in Poland. That factory still exists, although it was renamed the Opoczno Terracotta Products Factory in 1950 and is today just called Opoczno S.A. The company's symbol is known in the heraldic world as a pierced mullet star, as is not unusual for porcelain marks and coats of arms around Europe."

Moreover, Colls was aware "that the tile was made by Dziewulski i Lange—because she mentioned that on her official website dealing with the excavations", and so this is deliberate fraud rather than amateurish incompetence and ignorance. Colls decided to dig at a spot which is known to be a cemetery ten minutes' walk south of Treblinka 1, which is therefore further proof of deception. And after hours of digging and disturbing a burial site merely in order to engage in fraud, Colls' team not surprisingly found the grand sum of "40 bone fragments" - hardly proof of mass graves of 800,000 bodies!!!

CollsTreblinkaFraud photo CollsTreblinkaFraud_zps317fde0a.png

Source: The New Observer

Some people simply watch TV and read newspapers, and either don't have internet access, or merely use the internet for entertainment. So Hoaxers cynically calculate that their benefits from deceiving a few of these blissfully ignorant people exceeds their costs of revealing further proof of their deliberate lies and deceptions to people who are already sufficiently well informed to know that the whole "Holocaust" "gas chambers" legend is the greatest hoax of the twentieth century, a modern-day religion that foments fear and hatred, and a myth based on a pack of lies concocted by money-grubbing, hate-filled racists for business and political purposes.

For decades, after abandoning "steam chambers" and "electric plates", Hoaxers were claiming that Jews were murdered at Treblinka, Belzec, Sobibor and some of the other alleged "death camps" by carbon monoxide in Diesel exhaust fumes. There is a chapter in Dissecting the Holocaust by Friedrich Paul Berg: "Diesel Gas Chambers: Ideal for Torture - Absurd for Murder". Hypothetically, Diesel exhaust can kill, but it is an absurd choice as a means of mass murder. In contrast to the gasoline engine, Diesels operate with excess air, so that there is relatively little incomplete combustion of fuel, and exhaust CO levels are relatively low. In order to achieve low enough oxygen levels and sufficient CO to kill all those in the "gas chamber" within half an hour or so, the engine would have to be operating at close to full load. Berg says:

"One might think that all one has to do to get a high fuel/air ratio is to press the fuel pedal to the floor - without any external load being coupled to the engine. What happens then, as the fuel pedal is simply pressed 'to the metal,' is that the fuel/air ratio will indeed go to the maximum that the fuel injection stop setting will allow and, because of that, the engine speed will rapidly increase as well. Within a few seconds, the engine speed will approach the maximum safe engine speed set by the manufacturer. Long before that speed is reached, however, an internal speed governor in the fuel injection pump assembly will restrict the fuel supply - and quite severely - to protect the engine by ensuring that the maximum safe engine speed or 'redline' speed is never exceeded. The actual fuel/air ratio at 'high speed idle' will stabilize after a few seconds, since there is no load, to nearly the exact same low fuel /air ratio as at 'low speed idle.' At high speed idle, more fuel will be consumed per second, but because more air is also being drawn into the engine, the fuel/air ratio will remain nearly the same as at low speed idle. In other words, pushing 'to the metal' without an external load will not raise the fuel/air ratio, except initially.

[...] To impose a substantial load on any engine is far from easy. For example, if one has an ordinary truck, a full load can be imposed on the engine by first filling the truck with a heavy cargo and then racing the vehicle up a steep hill with the fuel pedal to the floor. Under that condition, one would probably be putting out about 0.4%/vol. CO, which is indeed lethal, from the exhaust pipe of an undivided chamber Diesel. However, if the truck is simply parked in a driveway, it is practically impossible to impose any significant load on the engine. Merely 'racing' the engine with the transmission in neutral will impose no more than a few percent of load. Letting the clutch slip and stepping on the accelerator may impose a somewhat greater load on the engine - but the clutch will rapidly burn out. Jacking up the rear end of the vehicle and applying the brakes while racing the engine will impose a somewhat greater load, but the brake linings will rapidly burn out."

Further proof of Hoaxers' lies and deceptions is hardly necessary, but these fake "eyewitnesses" to Diesel exhaust murders claimed to have seen "gassing victims" with their skin turned blue. As the Encyclopaedia Britannica states for carbon monoxide poisoning, "Carboxyhemoglobin has a characteristic cherry-red colour. In spite of asphyxiation, cyanosis (turning blue) does not occur; the skin is pink or pale and the lips bright red." But the "eyewitnesses" did not know that, and are thereby revealed as liars who were too ignorant to concoct a credible fiction to prop up their allegations. People who were "gassed" with Diesel exhaust fumes from an engine that was not heavily loaded would have got a headache after more than half an hour, and some would have gone on to die from cancers in another 40 years or so, but they would not die immediately, making it an entirely unsuitable mechanism for mass murder. Although oxygen levels in the exhaust would be relatively low (hence, moderate headaches after an hour or so), the exhaust would supply the "gas chambers" with enough oxygen to keep the prisoners alive, whereas the "evil" 'Nazis' could have simply left the prisoners to asphyxiate in an airtight chamber, speeding up the process, with no need to bother with engines, fuel, hoses, and extracting CO before going in to drag out the bodies. After the Diesel exhaust fumes stories were debunked, some Hoaxers quietly abandoned them for new claims of mass murder by gasoline exhaust (which are still refuted by the demonstrably false reports about skin color). But since gasoline contradicted the "eyewitnesses'" statements, Hoaxers now claim Diesel some of the time and gasoline the rest of the time, depending on who they are trying to convince.

Hoaxers' metaphysical conspiracy theory of a "meeting of minds"

One of the more amusing features of the Hoaxers' conspiracy theory is how it requires "an incredible meeting of minds" and "mind reading" as if by "telepathy", which is a consequence of the fact that there were no written orders, no blueprint, and no budget, for an extermination program. Hoaxers have distanced themselves from history and have moved on to metaphysics, which is hardly sufficient basis for accusations of mass murder. In February 1983, Jewish Hoaxer "historian" Raul Hilberg summarized his 'thesis' before an audience of nearly 2,700 at Avery Fischer Hall in New York City.

"But what began in 1941 was a process of destruction not planned in advance, not organized centrally by any agency. There was no blueprint and there was no budget for destructive measures. They were taken step by step, one step at a time. Thus came about not so much a plan being carried out, but an incredible meeting of minds, a consensus-mind reading by a far-flung bureaucracy."

Somehow, it is asserted, those "evil Nazis" just knew that six million Jews had to be killed, and went ahead and did it, without any worries over possibly incurring the wrath of their leaders. (Here, we must suspend disbelief and forget that there were only around three million Jews in German-controlled territory in 1941, as pointed out by Roger Dommergue and others.) The total absence of any traces of written documentation relating to a "Nazi" extermination program, the total absence of any photographs or film footage of a "gas chamber", and the total absence of any autopsy on any concentration camp casualty demonstrating death by gas poisoning is of course in stark contrast to the existence of written documentation of a Jewish program for world conquest - which was discovered in the 19th century in the document known as the Protocols of Zion, and confirmed by its correspondence to the world about us, such as Jewish control of the press, servile politicians sucking up to Israel and Jewish pressure groups, and so on.

Hilberg's magnum opus, his work on the "Holocaust" entitled The Destruction of the European Jews, was dissected by Jürgen Graf in his book The Giant With Feet of Clay. For example, in Hilberg's gigantic work, which by the 1985 revision had expanded to a three-volume, 1,274-page set, there is not one photograph or illustration in the text; the only photographs are on the title pages of the three volumes. Extraordinarily, there is no description of a "gas chamber" or "gas van", and in contrast to many revisionists who visited the alleged "extermination camps" to conduct research, from 1948 to 1985 Hilberg only ever spent one day at Treblinka, a half-day at Auschwitz I and at Auschwitz-Birkenau, and in all cases it was only to participate in memorial ceremonies. He never visited any of the other concentration camps. Most of his work is about "persecution" of the Jews rather than the alleged "extermination", and there is very little about the so-called "Killing Center Operations".

HilbergNoPhotographs photo HilbergNoPhotographs_zpsdd64dcd4.png

Source: The Giant With Feet of Clay [Chapter 2], Jürgen Graf

Jewish fairy tales of how "German methods" could circumvent mathematical and physical law

Chapter 7 is about Hilberg's claims regarding the "killing centers". Obviously, they're nonsense, but one of the most hilarious parts involves the claims and testimony of Charles Bendel, a Jewish "medical doctor". Bendel is the source for Hilberg's allegation that most of the Zyklon B in Auschwitz was used for "exterminating" the Jews (in contrast, the more moderate Hoaxer Jean-Claude Pressac said most Zyklon B was used for disinfestation). Graf reports on the reliability of Hilberg's various sources, and Bendel was testifying at the 1946 trial against Dr. Bruno Tesch and his assistant Karl Weinbacher - two innocent men whom Bendel helped send to the gallows. Here are Bendel's responses when cross-examined by Dr. Zippel, attorney for the accused:

Question: You have said, the gas chambers were 10 x 4 x 1.6 m large; is that correct?
Answer: Yes.
Question: That is 64 m³, is it not?
Answer: I am not quite sure, that is not my strong point.
Question: How can it be possible to fit 1,000 people in a 64 m³ room?
Answer: That is what you have to ask yourself. It can only be done with German methods.
Question: Do you seriously maintain that you can fit ten persons in a half cubic meter space?
Answer: The four million people gassed in Auschwitz are proof of it.
Question: When you say, they took 17 tonnes of gold from the corpses, are you basing that on a tonne of 1,000 kg?
Answer: Yes.
Question: Then do you also maintain that every victim, whether man, woman, child or baby, would have 4 grams of gold in his mouth?
Answer: It must have been that some had more and others less or even none; it would depend on the condition of their teeth.

This is the 'quality' of Hilberg's sources of information. Rather than forensic examinations, chemical analysis, scanning the soil for traces of mass graves, studying plans of the buildings, determining what is possible according to laws of nature, etc., Hilberg relies upon these "eyewitnesses" to obtain his politically motivated conclusions. When a Hoaxer says "with German methods", what he really means is "in Jewish fairy tales"!

If the average prisoner is "moderately thin" at 55 kg and has a similar density to water, then the volume of one prisoner is 0.055 m³, and the volume of 1,000 prisoners is 55 m³. At a packing density of 0.859, they need to have everyone lying on top of each other, piled up to the ceiling, relying upon unequal sizes, and having a better arrangement than a circle within a square - such as a hexagonal packing arrangement. Surely someone would have noticed that it's an odd way to take a shower!!!

The fallibility of human memory and perception, and the bias of "eyewitnesses"

Elizabeth Loftus, a Jewish cognitive psychologist and expert on human memory, tells in Witness for the Defense: The Accused, the Eyewitness, and the Expert Who Puts Memory on Trial (co-author Katherine Ketchum) of how memory is very fallible, and "eyewitness accounts can be and often are so distorted that they no longer resemble the truth". Loftus tells of a case with tragic consequences where perception was distorted by "prior expectations or interests" (there are some parallels with the Oscar Pistorius case):

"Two men in their mid-twenties were hunting for bears in a rural area of Montana. They had been out all day and were exhausted, hungry, and ready to go home. Walking along a dirt trail in the middle of the woods, with the night falling fast, they were talking about bears and thinking about bears. They rounded a bend in the trail and approximately twenty-five yards ahead of them, just off the trail in the woods, was a large object that was moving and making noise. Both men thought it was a bear, and they lifted their rifles and fired. But the 'bear' turned out to be a yellow tent, with a man and a woman making love inside. One of the bullets hit the woman and killed her. When the case was tried before a jury, the jurors had difficulty understanding the perceptual problems inherent in the event; they simply couldn't imagine how someone would look at a yellow tent and see a growling bear. The young man whose bullet killed the woman was convicted of negligent homicide. Two years later he committed suicide."

Loftus says, "Eyewitnesses who point their finger at innocent defendants are not liars, for they genuinely believe in the truth of their testimony....That's the frightening part--the truly horrifying idea that what we think we know, what we believe with all our hearts, is not necessarily the truth." And her work evokes admiration and fury. "One anonymous letter from an incest survivor concludes, 'Please consider your work to be on the same level as those who deny the existence of the extermination camps during WWII'." But Loftus had some important things to say about "Holocaust" "eyewitnesses", as in, for example, the malicious trial of John Demjanjuk (who, although falsely convicted of "28,060 counts of being an accessory to murder", died before his final appeal could be heard, and so does not have a criminal record under German law).

In his review of Witness for the Defense, John Cobden tells of how Loftus wrestled with her conscience when she went to Israel to sit in on the Demjanjuk trial, deciding not to testify.

"In her analysis of the trial, Loftus presents compelling reasons to doubt Demjanjuk's guilt. And even though, as she explains, she felt a professional obligation to come to the aid of the defendant, she ultimately decided not to do so. [...] When another 'eyewitness,' Eugen Turowski, was first questioned, he recognized Fedorenko but not Demjanjuk. However, when Turowski returned the next day for further questioning, and was again shown the photos, he announced that the picture of Demjanjuk was that of 'Ivan the Terrible,' the Treblinka sadist. [...] In all, just five witnesses identified Demjanjuk as 'Ivan the Terrible.' At least 23 former Treblinka inmates failed to identify him.

In the end, Loftus decided not to testify on behalf of a man she believed was very possibly innocent because she didn't want to offend her relatives, her friends, Jewish survivors and Jews everywhere. In short, as she acknowledges, Loftus put her Jewishness ahead of her regard for truth and justice.
If I take the case,' I explained, having talked this out with myself hundreds of times, 'I would turn my back on my Jewish heritage. If I don't take the case, I would turn my back on everything I've worked for in the last fifteen years. To be true to my work, I must judge the case as I have judged every case before it. If there are problems with the eyewitness identifications I must testify. It's the consistent thing to do.' p. 232)

Some "eyewitnesses" are obviously out-and-out liars, such as those who claim to have survived "gas chambers" six times. But many others had "prior expectations" after already being brainwashed by camp propaganda and rumors about "gas chambers", "steam chambers", "vacuum chambers", etc., which would have distorted their memories. And all "witnesses" had to choose between what they saw as betraying their Jewish heritage, or a possible betrayal of truth and justice. For some witnesses, who knew what they'd seen, this must have been an unenviable choice. But for those brainwashed into believing in the "extermination" myth and the legend of the "evil Nazis", the choice was easy: stick up for the Jewish "race" (or religion), and they came to imagine that they were also defending the truth. What is needed is a sea-change, so that people can learn how the evidence proves the "extermination" allegations are nothing more than a myth, and Jews can understand that by continuing to make themselves look like deliberate liars who slander the German people for profit and power, they are doing the very opposite of defending their Jewish heritage - and their human heritage, by laying the foundations for "anti-Semitism" and a potentially horrendous conflict between Jews and Gentiles that should never happen.

The reliability of 'confessions'

For more about the value of 'testimony' and 'confessions', see Dissecting the Holocaust, Manfred Köhler, "The Value of Testimony and Confessions Concerning the Holocaust". For example, some of the methods employed to elicit 'confessions' include:

skin burns
destruction of the bed of the (finger-, i.e., toe-)nails with burning matches
torn-out fingernails
knocked-in teeth
broken jaws
crushed testicles
wounds of all kinds due to beatings with clubs
brass knuckles and kicks
being locked up naked in cold, damp and dark rooms for several days
imprisonment in hot rooms with nothing to drink
mock trials
mock convictions
mock executions
bogus clergymen, and many more.

Germar Rudolf openly admits that "Manfred Köhler" was one of his pseudonyms at a time when he was "rather busy" (not to mention being persecuted by those who fear the truth). Harry Mazal, a Jewish founder member of the Congregation Israel of San Antonio synagogue who got into the Shoah business and built a library and a propaganda website to sell his false version of history, had the audacity to claim Rudolf's use of pseudonyms was 'evidence' of "intellectual dishonesty" and an "attempt to obfuscate and confuse". However, rather than revisionists, it's Mazal's Hoaxer chums who need to prop up their 'truth' by resorting to bombs, arson attacks, breaking jaws, extracting fingernails, burnings, beatings, castrations, lawsuits, extraditing people to another continent and jailing them for years merely for stating their opinions, and employing some pretty redhead to pose as a numbskull who digs at a cemetery, finds a few bone fragments and gets tearful when she imagines it's evidence that 900,000 were systematically murdered!!!

The last thing Hoaxers need is intellectual honesty; they know a level playing field assures their defeat.

(Interestingly enough, Harry Mazal, who died in 2011, was an expert in dynamite and was based in Mexico City for most of his life before moving to San Antonio, Texas. Israelis Salvador Guersson Smecke and Saur Ben Zvi were caught and arrested inside the Mexican Congress chamber in possession of dynamite, detonators, wiring, guns and grenades while posing as "press photographers" on October 10, 2001, three days after the launch of the war in Afghanistan, after a large-scale 37-nation poll of world opinion carried out by Gallup International had found a 94% majority of Mexicans were opposed to military intervention in Afghanistan.)

The beginning of the end for the Holohoax

In Dissecting the Holocaust, Professor Faurisson tells in the chapter "Witnesses to the Gas Chambers of Auschwitz" how Simone Veil, a Jewish "French" politician who survived the Auschwitz "factory of death", effectively admitted the absence of proofs, traces and even witnesses of the "gas chambers". On April 26, 1983, the Paris Court of Appeal had found Faurisson guilty for "harm to others" (for telling the truth), but had perfectly summarized his "logical thread" and his "reasoning" by specifying that, for him:

"...the existence of the gas chambers, such as usually described since 1945, conflict with an absolute impossibility, which suffices by itself to invalidate all the existing testimonies or, at the least, to stamp them with suspicion."

That's an excellent summary, except that the last nine words could be omitted. If multiple witnesses tell stories that are totally impossible, then it doesn't matter whether it's six, six thousand or six million witnesses - they are lying. Or deluded. End of story. The court concluded: "The value of the conclusions defended by Mr. Faurisson [as to the problem of the gas chambers] rests therefore upon the sole appreciation of the experts, the historians, and the public." Hoaxers were unhappy that Faurisson's work had been taken seriously, his point of view had been respected, and he wasn't found to have been lying, negligent, frivolous or wilfully ignorant in arriving at his conclusions. So two weeks later, in a May 7, 1983 interview for France-Soir Magazine, Veil said:

"What strikes me nowadays is the paradox of the situation: someone publishes a diary attributed to Hitler by sheer dint of publicity and a great deal of money without, it seems, taking very great precautions to assure himself of its authenticity, yet, at the same time, in the course of a trial brought against Faurisson for having denied the existence of the gas chambers, those lodging the complaint are obliged to apply a formal proof about the reality of the gas chambers. Yet everyone knows that the Nazis destroyed these gas chambers and systematically eradicated all the witnesses."

This followed a "dark year" for the Hoaxers. On April 21, 1982, an association was founded in Paris to research evidence for the existence and operation of the "gas chambers". However, they failed to discover any proof, and of course, never will. Then an international symposium on "Nazi Germany and the extermination of the Jews" was held at the Sorbonne, June 29 to July 2, 1982. It was supposed to serve as a decisive rebuttal to the revisionist offensive in France, concluding with a press conference that would strike a resounding blow. However, during the press conference, the two organizers shied away from even mentioning the words "gas chamber(s)". Faurisson thus dates as July 2, 1982, the time when "the myth of the 'Nazi gas chambers' and their associated witnesses died or entered their final death throes, at least on the level of historical research." So the Jewess Veil's admission that there was no evidence of gas chambers and no credible witnesses of gas chambers - and her attempt to 'explain' it with the claim that the 'Nazis' had "destroyed" the "gas chambers" and liquidated all the witnesses - came when the myth had already entered its death throes.

Also see Rudolf's Lectures on the Holocaust [p. 175 in the 2005 edition], a quote by Dr. Arno J. Mayer, Professor of Modern Jewish History at Princeton University, from his 1990 book about the "Holocaust" - Why Did the Heavens Not Darken?

"Sources for the study of the gas chambers are at once rare and unreliable.
Even though Hitler and the Nazis made no secret of their war on the Jews,
the SS operatives dutifully eliminated all traces of their murderous activities
and instruments. No written orders for gassing have turned up thus far. The
SS not only destroyed most camp records, which were in any case
incomplete, but also razed nearly all killing and crematory installations well
before the arrival of Soviet troops. Likewise, care was taken to dispose of
the bones and ashes of the victims."

As Rudolf puts it, Mayer's argument in principle boils down to: "The fact that there is no material evidence proves that this evidence was eliminated without a trace", which is the same line of argument used by other Hoaxers such as Simone Veil.

Along with the plethora of ludicrous claims that soon unravelled, such as "steam-filled chambers" and a "building where the floor was electrified in a special way", was the allegation that work camps in Germany proper, such as Dachau and Buchenwald, were "extermination camps" where gassings occurred. Unfortunately for the Hoaxers, people were able to visit those camps, and were able to see for themselves that the allegation was a lie. Hoaxers now have to resort to claims that the Dachau "gas chamber" was merely "in the process of being built", but it was "never completed", and concede that no gas chamber was ever used there. So the same ultra-efficient Germans who were supposedly capable of burying 870,000 Jews at Treblinka, and then digging them all up and cremating every one within seven months to get rid of the evidence, and murdering at least 1.3 million people at Auschwitz and cremating every one to get rid of the evidence, could not even build a gas chamber in Dachau after three years of attempts, even though "work was going on at a high speed"???!!!

After the vast majority of outlandish allegations had bit the dust and were recognised as the black propaganda of wartime, the remaining part of the Hoax that survived for decades was that about "death camps" and "gas chambers" in Poland. That legend only endured because Stalin and Beria, well aware that there were no "gas chambers" or "death camps", understandably wouldn't allow independent observers into the Iron Curtain to examine the 'evidence' of the "death camps". This gave the Soviets time, for example, to reconstruct an alleged "gas chamber" at Auschwitz after the war, as exposed by David Cole. The "gas chambers" part of the myth endured because there were delousing chambers, and so Jews could cite Zyklon B as the "murder weapon", even though it had been used to preserve life, not to exterminate.

How separation of family members helped to perpetuate the "gas chambers" myth

One reason why the myth persisted for so long is the fact that Jewish families were separated during the war, and in many cases each individual survived the war but sadly did not manage to locate other family members. They were brainwashed by the mass media into believing Hoaxer propaganda about the "evil Nazis" operating an extermination program - the "Holocaust" fable, and went on to presume that their missing relatives and friends must have perished in the "Holocaust". Google: jewish separated holocaust reunited, and there are numerous examples of people being reunited after 60 years, 65 years, and so on, often as a result of their "internet sleuthing".

See this YouTube video of a recent recording of David Cole (who went into hiding as "David Stein" after receiving death threats, until recently being outed) talking about the "Holocaust", Auschwitz and so on. At around twenty minutes, Cole tells how he was on the Montel Williams Show (in 1992) and they brought on Ernest Hollander, a Jewish fellow who'd been imprisoned in Auschwitz in 1944, along with his family. Hollander kept insisting that his brother had been killed, and how could Cole say that his brother was not killed. It turned out that the "exterminated" brother, Zoltan, had been fighting the Germans until the end of the war, but the Soviets thought he was a pro-German spy and sent him to Siberia for ten years. Then he returned home to Yugoslavia, where the authorities accused him of being a Soviet spy and mistreated him. For nearly 50 years, Ernest and his other brother Alex - both living in northern California - and scores of other relatives in the US, Canada and Britain, thought that Zoltan had been murdered. They had good reason for doing so, because a few years after the war, a 'friend' told Ernest that he'd witnessed Zoltan's execution in 1994 by German soldiers who'd hanged him from a tree. And as Cole says, the Jews imprisoned in 1944 were later told by Western governments that if they had any missing family members at the end of the war, then they must have been killed and there was no point in looking for them. Meanwhile, for all that time, Zoltan presumed that his entire family - who were the other side of the Iron Curtain - had perished in the war. It was only after a migrant from Serbia who was living in Brooklyn recognized Ernest on the screen as the "spitting image" of a friend he'd known back in Serbia, his upstairs neighbor by the name of Zoltan "Hershe" Hollander, that the family was reunited.

On November 17, 1992, a special session of the Montel Williams show was broadcast featuring the reunited Hollander brothers. But neither Cole nor Mark Weber, the other revisionist on the show, received the slightest thanks from any Hollander family member for bringing together the long-lost brothers. Ernest referred to Cole and Weber as "bums", and Williams reported that he'd been "deluged with complaints" about the April 30, 1992 broadcast. Jewish organizations had threatened law suits for allowing the two revisionists to appear.

Responsibility for the fact that many innocent Jews were not reunited with other family members for so long, or were never reunited, because they mistakenly imagined that they'd been "exterminated" and thereby had little or no motivation to search for them, and for the fact that many innocent Jews must have been worried - to put it mildly - that since there had apparently already been one "Holocaust" in their lifetime, there might be another, lies squarely with the lying, grasping, scheming, snivelling, parasitic Hoaxers, who gorge themselves on human misery like bed bugs gorge on human blood. (Anyone who propagated the lies due to mass-media brainwashing, ignorance, a lack of education, or general indifference to the world about them, is of course blameless. However, now that the Hoax has been widely debunked all over the internet and in dozens of books, those who continue to post lies on the internet, apart from making an idiot of themselves in public, are, ironically, contributing to Jewish misery as did the original Hoaxers.)

In Dissecting the Holocaust, the chapter "National Socialist Concentration Camps: Legend and Reality" [pp. 305-7], Jürgen Graf tells of how the Jewish "German" communist Bruno Baum admitted to being one of the main fabricators of propaganda at the Auschwitz camp. Baum was sentenced to ten years' imprisonment in 1935 for anti-government activity, along with Erich Honecker, who would later be president of the communist East Germany. In 1943, Baum was transferred from Brandenburg prison to Auschwitz. In the first edition of his memoirs, published 1949, Baum wrote [pp.34-5]:

"It is no exaggeration when I say that the majority of all Auschwitz propaganda, which was spread at that time all over the world, was written by ourselves in the camp. [...] We carried out this propaganda in [for] the world public until our very last day of presence in Auschwitz."

In the next edition, published 1957, Baum had changed that to:

"It is no exaggeration when I say that the greatest part of the publications on Auschwitz spread all over the world originated from ourselves [...] We informed the world in this manner until the very last day of our stay in Auschwitz." [p. 89]

As Graf says, "propaganda" became "publications", which "informed" the world. And on p. 308, Graf states:

"The orthodox historians are unable to explain why Jewish inmates who were allegedly destined for extermination were, in many cases, nevertheless transferred from one camp to another, without succumbing to extermination; or why Benedikt Kautsky, who, as a left-wing Socialist and Jew was doubly marked for extermination, survived Dachau, Buchenwald, Auschwitz, and, once again, Buchenwald; or why Israel Gutman, later co-editor of the Encyclopadia of the Holocaust, survived not only the "extermination camps" of Majdanek and Auschwitz but the "ordinary concentration camps" of Mauthausen and Gunskirchen as well;[124] or why the Polish Jew Samuel Zylbersztain survived to write a report entitled Memoirs of an Inmate of Ten Camps, describing his experiences in Majdanek, Auschwitz, and eight (!) other concentration camps.[125]

The orthodox historians must be deeply embarrassed by the release of 20,000 inmates from Majdanek "extermination camp," each one of which must have been a witness to the cruelty of the "mass exterminations," if any such exterminations ever took place there; or by the fact that the National Socialists released large numbers of inmates in the summer of 1944, in the midst of the alleged extermination of the Hungarian Jews. They cannot explain either why the Germans, during their withdrawal from Auschwitz-Birkenau, left 4,299 inmates behind, almost all of them Jewish, each of whom would have been an accuser of the Third Reich if the official version of Auschwitz squared with the historical facts.

In short: the orthodox history of the National Socialist concentration camps has reached the point of collapse."

The long history of allegations of a "holocaust" and "six million" "exterminated" Jews, from 1891 to 1945

In 1898, Rabbi Stephen Samuel Wise attended the Second Zionist Congress in Basle, where he met Theodor Herzl, instantly "felt a bond with him", and "agreed to serve as American secretary of the world Zionist movement". The New York Times reported that Wise spoke of "six million living, bleeding, suffering arguments in favor of Zionism", at a Federation of American Zionists meeting at Cooper Union in Manhattan on June 10, 1900. Wise campaigned for President Woodrow Wilson in 1912, helped write the "British" Balfour Declaration of 1917 along with Louis Brandeis and Felix Frankfurter, and helped to persuade Wilson to support the Balfour Declaration. From 1916 to 1919 Wise was "an important liaison between the American Jewish community and President Wilson". Thus, Wise was a rabid Zionist who regarded "six million" dead or dying Jews as a pretty good argument for Zionism.

On April 18, 1938 [p. 15] - before WWII had even started! - the New York Times quoted Wise as saying: "[Christ] died as millions of Jews are dying today".

Rabbi Wise was the president of the World Jewish Congress from 1936 until his death in 1949. The New York Times of June 30, 1942 [p.7] ran an article:

"1,000,000 JEWS SLAIN BY NAZIS, REPORT SAYS

LONDON, June 29 (U.P.) ... spokesmen for the World Jewish Congress charged today.

They said Nazis had established a 'vast slaughterhouse for Jews' in Eastern Europe ...

A report to the Congress said that Jews, deported en masse to Central Poland from Germany, Austria, Czechoslovakia and the Netherlands were being shot by firing squads at the rate of 1,000 daily.

Information received by the Polish Government in London confirmed that the Nazis had executed 'several hundred thousand' Jews in Poland."

The Pittsburgh Post-Gazette carried the story on the same day, alleging 700,000 Jews murdered in Lithuania and Poland, 125,000 in Rumania, 200,000 in Russia, and 100,000 in the rest of Europe.

So, in June 1942, Hoaxers allegedly know how many Jews have been killed in each country, but they daren't name specific camps such as Auschwitz, since they know that would allow the Germans to refute the claim and prevent their legend from getting airborne. After the war, it supposedly takes them another 45 years to revise the claimed Auschwitz death toll by nearly three million! Wise's claims of June 1942 didn't prove sufficiently convincing, and so in August he decided to try a more sophisticated approach.

On August 28, 1942, Rabbi Wise received a telegram from Sidney Silverman, a "British" Jewish Member of Parliament, relaying "information" from one of several telegrams which had originated earlier that month from Gerhart Riegner, the World Jewish Congress representative in Geneva. The message included:

"RECEIVED ALARMING REPORT THAT IN FUHRERS HEADQUARTERS PLAN DISCUSSED AND UNDER CONSIDERATION ALL JEWS IN COUNTRIES OCCUPIED OR CONTROLLED GERMANY NUMBERING 3-1/2 TO 4 MILLION SHOULD AFTER DEPORTATION AND CONCENTRATION IN EAST AT ONE BLOW EXTERMINATED TO RESOLVE ONCE FOR ALL JEWISH QUESTION IN EUROPE. STOP ACTION REPORTED PLANNED FOR AUTUMN METHODS UNDER DISCUSSION INCLUDING PRUSSIC ACID"

Riegner claimed to have received information of an impending "extermination" plan from some anonymous German industrialist, still anonymous at the time Arthur Butz wrote The Hoax of The Twentieth Century in 1976 (the 2003 edition reproduces the old text but includes supplements and a 2003 Foreword). In 1986, the "industrialist" was claimed to be Eduard Schulte, by "Holocaust historian" Richard Breitman and Jewish "historian" Walter Laqueur. Schulte, who died in 1966, is alleged to have been an agent for US intelligence supremo Allen Dulles. Interestingly enough, Dulles is himself named as the intermediary said to have discovered the White Russian landowner with English connections, the mysterious "Mr. X", the "source" provided to Philip Graves in 1921 for the Times 'exposé' that made the risible assertion that since passages in the Protocols of Zion were plagiarised from passages in Maurice Joly's Dialogues, the Protocols was a 'proven' "forgery". If "information" was needed, Dulles would "discover" it, and the "source" would be attributed to an anonymous or dead person, thereby eliminating any possibility of the "source" denying involvement.

At the time, everyone was well aware Riegner's rumor was a hoax and didn't take it seriously. However, after the war, when Allied governments needed to deflect attention from their own war crimes such as Dresden by portraying the Germans as barbarians who committed terrible crimes against humanity, and when Jews needed to promote their Holohoax in order to get their paws on Palestine, and Jews were able to mould public opinion through their control of the press and Hollywood, the unholy alliance of war criminals, corrupt politicians and a nation without a land colluded in rewriting history. This time, in the brave new 'reality' of victors' justice, the Reigner telegram had transformed into genuine "information", and sadly, no one had taken it seriously.

This paved the way for irrelevant, distracting debates over whether or not Rabbi Wise should have done more to try to convince people that there really was a "Holocaust", whether Allied governments, the Pope, or the Red Cross should have done more, and so on, rather than the debate that should have been raging on whether human bodies could be burnt with negligible fuel, whether the 'Nazis' could possibly have been stupid enough to employ 99.9% of their Zyklon B for saving Jews when they were using the other 0.1% to kill them, whether 1,000 people could be fitted in a 64 m³ room even with "German methods", how an extermination program to kill six million people could be carried out with no budget, no written orders and without leaving a trace, whether the 'Nazis' had "telepathic" powers, how long it would take the brake linings or the clutch to wear out on a Diesel-engined vehicle that was being run at close to full load to generate carbon monoxide, whether the Germans could have been stupid enough to employ such a preposterous method of CO generation, how Jewish slave laborers on starvation rations could perform as woodcutters at 81 times the productivity that experienced woodcutters attained in peacetime, how mass open-air cremations could be made invisible to Allied aircraft, whether six million people could have been murdered - mostly by gassing - when there was not one autopsy confirming a "gassed" victim and not one photograph or piece of film footage of a "gas chamber", how a "gas chamber" that required holes in the roof through which Zyklon B would be dropped could work when it had no holes in the roof, did it make sense to transport Jews to an occupied nation merely in order to kill them, did it make sense to have a hospital at a "death camp", why believe any of the allegations when it was already accepted that well over 90% of Hoaxers' claims - death camps in Germany proper, death by quicklime, steam chambers, vacuum chambers, electric plates, drowning, atomic bomb, pedal-operated brain-bashing machines, a bear and an eagle, etc., - were a total pack of lies and the rumor promoters had already resorted to forgeries, and so on.

As an indicator of the 'reliability' of "information" emanating from the World Jewish Congress around the time that Riegner's rumor was being circulated, the American and British branches of the WJC allegedly received a 'report' from the Swiss branch of Agudat Israel on September 4, 1942, claiming Jews were being deported from the Warsaw ghetto for resettlement in the East. The 'report', written by someone posing as a paranoid conspiracy nut, falsely suggested that "resettlement" was a euphemism for murder, and claimed, "The corpses of the victims are used for the manufacture of soaps and artificial fertilisers."

Thus, we have Stephen Samuel Wise, a rabid Zionist who regarded "six million" dead or dying Jews as a pretty good argument for Zionism back in 1900, heavily involved in fabricating the initial claims of a National Socialist "extermination" policy in 1942, just when Zionists desperately needed to sell the idea of a Jewish "holocaust" in order to trick the world into letting them have Palestine, ostensibly as a sanctuary for Jews. "Zionism" was itself merely a means to an end. There was the Jews' imperialist dream of establishing a Jewish "Utopia", as described in Michael Higger's The Jewish Utopia (1932), in which the "righteous" - i.e., the Jews - would inherit the world's riches. And running in parallel was the Rothschild dynasty's dream of world conquest which began when Mayer Amschel Rothschild observed how William I of Hesse, later known as William IX, Landgrave of Hesse-Kassel, and his father made a fortune from hiring out Hessian soldiers to foreign countries for profit, for example, to Britain's King George III to fight in the American War of Independence, saw how they profited whichever side won the war, saw that Adam Weishaupt's Illuminati policies of exploiting secret societies, attacking the nation-state and religion would also be useful (but of course adapted the latter so as to attack Christianity and Islam whilst promoting Judaism), and drew up instructions for his five sons. For anyone seeking world domination, however much political power they already had, the additional clout from having their own sovereign state would always be very valuable. If most of their people came from Khazaria, for example, rather than the Middle East, they would simply lie about their origins. After all, lying is their forte!

After the Hoaxers had succeeded in getting their myth of a Jewish "holocaust" accepted as 'reality', it would become known as "the Holocaust".

On October 13, 1919, the American Hebrew ran an article that was attributed to Martin H. Glynn: "The Crucifixion of Jews Must Stop!"

"From across the sea six million men and women call to us for help, and eight hundred thousand little children cry for bread. [...] Six million men and women are dying from lack of the necessaries of life; eight hundred thousand cry for bread. And this fate is upon them through no fault of their own, through no transgression of the laws of God or man; but through the awful tyranny of war and a bigoted lust for Jewish blood. In this threatened holocaust of human life, forgotten are the niceties of philosophical distinction, forgotten are the differences of historical interpretation..."

Now in theory, it's possible that Glynn's reference to a "holocaust", more than twenty years before Jews would go on to claim that "six million" Jews had been murdered in a "Holocaust", was a bizarre coincidence. And Glynn's reference to "six million" dying Jews - after Rabbi Wise said "six million" dead or dying Jews would be a pretty good argument for Zionism - was another unlikely coincidence. And Glynn just happened to be a Gentile who admired the Jews because he sincerely thought they were great. And his love for the Jews prompted him to write the American Hebrew article in 1919. But does all of that seem likely, or is there a better explanation?

Martin Henry Glynn (1871-1924) was Governor of New York from 1913-1914, after his predecessor William Sulzer became the first person ever to be impeached on dubious grounds for acts allegedly committed before taking office. Glynn was a correspondent of Abraham Jacobi (1830-1919), a German-born Jew who, as a member of the revolutionary movement in Germany, was imprisoned from 1851 to 1853, eventually being convicted of treason. Jacobi sailed to England on his release, where he stayed with Karl Marx and Frederich Engels, then went to New York where he became a practising physician. He founded the New York Communist Club in 1857. Although Jacobi went on to specialize in pediatrics, he practiced general medicine, surgery, and obstetrics in New York because "medical specialization was frowned on as being degrading". In 1900 a "Festschrift" was published in recognition of Jacobi's prolific contributions to medical literature. In Transactions of the Medical Society of the State of New York for the year 1905, Jacobi wrote an article: "The History of Cerebro-Spinal Meningitis in America".

Glynn sustained a spinal injury, for which he traveled to Germany for treatment in the spring of 1906. He was afflicted with chronic back pain for the rest of his life, and committed suicide in 1924, following a trip to Boston and an unsuccessful attempt to relieve his suffering. If Jacobi had been treating Glynn for his chronic condition, or had referred him elsewhere for treatment, either of which had provided some relief, this could account for Glynn's Judeophilia. In January 1914, Glynn wrote to Jacobi, appointing him as a delegate from the State of New York to the Congress in Berlin "protesting against the violations of the Berlin Treaty of 1878, which guaranteed full rights of citizenship to all Jewish subjects" who were "worthy people" upon whom a "great wrong" was being perpetrated. The American Hebrew piece was published three months after Jacobi's death, but as a Judeophile, Jews would have found it easy to persuade Glynn to write the article, whilst they provided tips on words and phrases to include. Or Glynn would put his name to a ghostwritten piece. It doesn't matter whether Glynn sincerely admired the Jews, or agreed to play along because he was under obligation. The best explanation for Glynn's apparent prescience of a "holocaust" of "six million" in 1919 is that Zionist Jews wanted to float the idea in the wake of WWI.

There were many claims on the theme of a "holocaust", "extermination", "annihilation" or "massacre" of the Jews, or of "six million" Jews who were being persecuted, starving, dying, etc., and most of these claims were made years or even decades before Adolf Hitler came to power. Here are a few reports from The New York Times. Note how, as early as March 1906, Jews are already 'predicting' a "systematic and murderous extermination" of "6,000,000 Jews". And then, by September 1919, a month before Martin Glynn's article, Jews are asserting that "6,000,000" Jews are going to be "completely exterminated". And by January 1945, one of Stephen Wise's cronies supposedly already knows that "six million" Jews have been killed, four months before the war ended in Europe, and 45 years before Hoaxers would go on to claim that this time, they really weren't exaggerating, and they'd got the Auschwitz death toll correct to the nearest million.

January 26, 1891; this is from an address by Rabbi Dr. Gustav Gottheil, who alleges that Russian Christians are persecuting "5,000,000 to 6,000,000 Jews": "...and the fact that about six millions persecuted and miserable wretches remain steadfastly faithful to a religion that causes their life to be changed into a fiery furnace without the angel to keep it cool is the nearest approach to a grandiose miracle that has been vouchsafed to this unbelieving generation."
March 15, 1896; this is again about Russian Jews: "...the Jews are 5,000,000 or 6,000,000. Mr. Thompson tells the pitiful tale of Jew-baiting with sympathy and moderation. [...] The harrying of the Jews is generally admitted to be one of the causes of the growth of poverty of the Russian people. M. Ewera mentions that, after the expulsion of the Jews from Moscow, the rate of interest in private pawnshops rose from 25 to 200 per cent. per annum."
May 16, 1903; this is about the "Kishinev Massacre" in which 49 Jews were allegedly killed according to the Jews. So when 49 Jews are killed it's a "holocaust" or a "massacre", when Israel kills 34 Americans and wounds 174 in a sustained attack on the USS Liberty it's an "accident", when Jewish terrorists dressed as Arabs blow up the King David Hotel killing 91 people it's the fault of the "British liars" for refusing to take heed of a warning, and when Israel murders nearly 2,000 Palestinians, mostly civilians, in Gaza in a month, they don't count because they "deserve to be dead" and they "were the ones with very low IQs": "The Jews concealed themselves in all manner of places, whence they were dragged out and killed outright or crippled. [...] 'We charge the Russian Government with responsibility for the Kishineff massacre. We say it is steeped to the eyes in the guilt of this holocaust. [...] So long as a 'civilized' Government brands 5,000,000 people as a perilous pest which must be slowly annihilated, so long its baser subjects will think themselves justified in accelerating the process of extermination with knives, axes and hatchets'."
January 29, 1905; the Jewish preacher Dr. M.H. Harris reveals Zionists need a "free and a happy Russia" like they need a hole in the head, since it could mean the end of Zionism! In other words, as Herzl said, the "anti-Semites" are the Zionists' best friends: "He declared that a free and a happy Russia, with its 6,000,000 Jews, would possibly mean the end of Zionism, since the abolition of the autocracy would practically eliminate the causes that brought Zionism into existence."
November 13, 1905; this includes a conspiracy theory proposed by the Rev. Dr. Joseph Silverman, who claims there was an organized conspiracy between the Czar, the bureaucracy, and the Russian Greek Church to massacre Jews. And Silverman says in a sermon at Temple Emanu-El: "The handwriting on the wall of the palace reads the doom of the Czar. [...] As at Kishineff, the Government was an abettor of the crime, so also now I can read the events of the past few months coupled with those of the past in no other light. This holocaust of Jews is but the culmination of the demand of the people for liberty." At a mass meeting, Dr. Madison C. Peters claimed, "...And now the reactionaries in Russia want the Jews exterminated, in the knowledge that while they remain there they will be a light in the darkness and the leaven of liberty which will in time leaven the whole lump so that in the long run despotism there shall be impossible."
December 5, 1905; this includes Joseph Silverman again at Temple Emanu-El; he bewails the "awful horrors" in Russia and mourns the "murdered" Jews. Then Louis Marshall's address includes: "Five millions of men, women, and children, coming from the same stock, praying to the same God, intrusted with the same mission as we, stretch out their hands - not for alms, but for an opportunity to help themselves. [...] Terrible as has been the holocaust, there is hope in the outlook. The Jew of Russia has learned the art of self defense. By the possession of arms, he has become conscious of his manhood."
March 25, 1906; this tells of how the Berlin-based Jewish publicist Dr. Paul Nathan was peddling the same conspiracy theory as touted by Joseph Silverman about a Russian government plot to exterminate "Russia's 6,000,000 Jews". Nathan claims that the Russian government planned "systematic and murderous extermination" of "6,000,000 Jews" as a "solution" to the "Jewish question". A few decades later, Jews would go on to accuse Hitler of actually perpetrating the very same "solution"! The Times report states: "STARTLING reports of the condition and future of Russia's 6,000,000 Jews were made on March 12 in Berlin to the annual meeting of the Central Jewish Relief League of Germany by Dr. Paul Nathan, a well-known Berlin publicist... [...] He left St. Petersburg with the firm conviction that the Russian Government's studied policy for the 'solution' of the Jewish question is systematic and murderous extermination. [...] He concluded with an appeal to the Jewish money powers of the world to arrest Russia's career as a borrower."
April 11, 1910; in an article headlined "Russian Jews in Sad Plight", the Rev. Dr. J.L. Magnes says, "The condition of Russia is worse today than at any time since the barbarous massacres and pogroms of 1905 and 1906. [...] Even though news was supplied [by the Russian government] the story of Jewish misery in Russia is such an oft repeated tale that hardly any attention is paid to it any more. But the condition of affairs is getting to be so fearful that it becomes necessary to raise our voice in protest and to appeal to the conscience of our fellow-citizens to take cognizance of the systematic, relentless, quiet grinding down of a people of more than 6,000,000 souls." (So here, the Russians are accused of carrying out a "systematic" repression of 6,000,000 Jews, more than 30 years before the Germans are accused of a "systematic" "extermination" of 6,000,000 Jews.)
October 31, 1911; tells of how "ministers and rabbis joined in passing resolutions pleading with Russia to stop her persecutions of the Jews...": "The 6,000,000 Jews of Russia are singled out for systematic oppression and for persecution by due process of law. [...] They are restricted in occupations, reducing many to starvation."
December 10, 1911; this is from a long report by Herman Bernstein, a Jewish writer who made several failed attempts to refute the Protocols of Zion: "The Russian Government, aside from the restrictive laws now in existence, has numerous other methods by which it intensifies the oppression of the Jews, and by which it is making the 6,000,000 Jews a people economically exhausted - a people without any rights at all."
October 29, 1916; this is about a campaign to raise $10,000,000 for the relief of "Jewish war sufferers": "Dr. Magnes has been enabled not only to learn the disposition of such funds as have already been contributed, but has gained first-hand information as to the present needs of the Jewish people in Europe, who have fallen under the blight of the world holocaust."
September 24, 1917; this is about "An appeal for a fund of $1,000,000 to alleviate the suffering of Jews in the European war zones". The American Jewish Relief Committee sent out an appeal including the statement: "We cannot help the men in the trenches or at the front, but the aged and infirm, the women, children, and babies at home must be saved if the Jewish race is to survive the terrible holocaust of the world war."
September 8, 1919; this is around five weeks before Martin Glynn's American Hebrew piece about "six million" "dying" Jews; Herman Bernstein is one of the speakers at a convention held by the Federation of Ukrainian Jews in America, where it is alleged that "6,000,000" Jews were going to be "completely exterminated": "Tales of massacres in which 127,000 Jews had either been killed or wounded during the last six months were told by the speakers [...] The President [Joseph Seff] reported that there were 3,000,000 Jews in Ukrainia and a like number in Poland, all of whom were in need of assistance from America. [...] This fact that the population of 6,000,000 souls in Ukrainia and in Poland have received notice through action and by word that they are going to be completely exterminated - this fact stands before the whole world as the paramount issue of the present day."
May 9, 1920; here, they admit that typhus is the main threat, rather than "extermination": "The campaign for $7,500,000 to relieve Jewish war sufferers in Central and Eastern Europe, which was to have closed last night, is to be continued another week. [...] Though more than $30,000,000 has been raised by the Jews and disbursed both among Jews and non-Jews abroad, the need today is more pressing than ever because to famine and distress in some of the stricken districts has been added the dread spectre of typhus, and to abandon the sufferers now or to apply half measures in succoring them would mean that some 6,000,000 men, women and children would be exposed to the menace of awful death." (Hoaxers sometimes contend that the "six million" in Glynn's article isn't really six million because it doesn't include the children; here, the children are included in the "six million" total.)
May 16, 1920; includes important material about typhus and delousing: "The effort to raise $7,500,000 to be expended in relieving the woe which already has descended upon thousands of stricken Jews in Central and Eastern Europe and which threatens 6,000,000 people if famine, disease and industrial prostration are not relieved promptly, enters today upon its third week with the amount needed far from subscribed. [...] A discussion of what is being done to combat typhus says: 'The Joint Distribution Committee is co-operating with the Polish Government and all relief organizations in the anti-typhus battle. It has appropriated $100,000 to be placed at the disposal of the Polish Government to buy coal with which to place in operation the American Army's delousing machinery now in Poland, the most effective single weapon against typhus fever. It has sent to Poland Dr. Harry Plotz, one of the world's foremost experts on typhus fever, the discoverer of the fact that typhus is spread by body lice, and who gave to the world the first successful anti-typhus serum'." Thus, the Americans and the Poles were well aware that delousing machinery was in Poland, and of its benefits; the Americans supplied it! Yet when the Germans use delousing machinery in Poland to protect their slave labourers against typhus, they're accused of "gassing" and "exterminating" them, because the victors get to write the 'truth'!!!
July 20, 1921; this returns to the theme of "extermination", and to make clear that it's not extermination by famine or poverty, it's "extermination by massacre": "Russia's 6,000,000 Jews are facing extermination by massacre. As the famine is spreading, the counter-revolutionary movement is gaining and the Soviet's control is waning. [...] The information was gathered by Dr. Joseph Kreinin, a noted Jewish social worker and President of the Russian Joint Board of Jewish Societies. He says that several villages have been burned already and scores killed, seventy in one village alone." So let's get this straight. This is within four years of Jewish Bolsheviks staging a coup d'état in Russia and turning it into a totalitarian state so they could loot the country and massacre the nobility, Jacob Schiff provided Trotsky with $20,000,000 in gold and Max Warburg provided Lenin with $6,000,000, Jews murdered the entire Imperial family in cold blood, typical reports on Jews' treatment of the peasants said, "As a result of refusal of 4,000 labourers near Ekaterinburg to support local Bolsheviks many were arrested, and twelve were suffocated alive in slag gas-pit, their mutilated bodies being buried afterwards, and ninety peasants taken out of Ekaterinburg prison, where they had been thrown because they objected to Bolsheviks requisitioning their cattle, &c., were brutally murdered." And: "The Bolsheviks had shattered the skulls of thirty-three of the bodies, so that the heads hung like bits of wood on the trunks. As well as being shot, most of the murdered had been pierced with bayonets, the entrails torn out, and the bones of the arm and leg broken." Then, when the people are fighting back and there is a chance of Jews tasting some of the medicine that they've already dished out, they start wailing and whining about "extermination" and "massacre", as if they're being unfairly picked on by people who simply hate Jews for no reason at all. It's rather like someone going up to a hornets' nest, starting to swat them, and then crying, "Why are they picking on me?" Of course, it's not fair that Russian Jews should have to pay a price if they weren't personally involved in atrocities, but justice is not so finely tuned in a less than ideal world.
May 31, 1936; this is well into TNYT's pay-per-view dates for most articles; this was six years before anyone was supposed to know that there was going to be a "Holocaust". The article includes: "Great Britain has it within her power to throw open the gates of Palestine and let in the victimized and persecuted Jews escaping from the European holocaust."
January 8, 1945; four months before the surrender of German forces in Europe - and 45 years before Hoaxers would claim to have at long last got the Auschwitz death toll correct to the nearest million after revising it down by three million - Dr. Jacob Lestchinsky, the Jewish economist and publicist, who interestingly enough headed the Economic Research Department of Stephen Wise's World Jewish Congress, claimed that "6,000,000" Jews had been killed in an article headlined "6,000,000 JEWS DEAD; Jacob Lestchinsky Estimates Reduction in Europe Since '39". The report said: "The Jewish population in Europe has been reduced from 9500000 in 1939 to 3500000, it was estimated yesterday by Jacob Lestchinsky, exiled economist and ...".

Jewish propagandists claim there was another massacre of the Jews at Bethar in the revolt of Bar Kokhba against the Romans. The Babylonian Talmud (Gittin 57b) states "...the Emperor Vespasian who killed in the city of Bethar four hundred thousand myriads, or as some say, four thousand myriads." In classical history a myriad is 10,000, so that is claiming between 40 million and 4 billion Jews killed. According to Jewish legend, the Romans kept on killing "until the horses waded in blood up to their nostrils and the blood moved stones the size of forty se'ah [293 liters] and flowed into the sea for a distance of forty miles (Lamentations Rabbah 2:79)". Thus, Jewish allegations of "massacres", "annihilations", "holocausts", "exterminations", and "persecutions" against them are as old as the hills, are part of their standard modus operandi, and should be afforded the same credibility as someone who tells you that when they were a lad they had to live in a shoebox and eat freezing cold gravel. If there really had been so many of these "holocausts" of the Jews over the last few thousand years, the Jews would have already been wiped out.

In 1919 they already know that "six million" Jews are going to be "completely exterminated", i.e., they've got it to the nearest 100,000 or so, but then it takes them until 1990 to get the Auschwitz death toll correct to the nearest million??????

Jewish agitators - the real cause of World War Two

Almost immediately after Hitler was elected as the Reich Chancellor on January 30, 1933, Jews who had fled abroad with their fortunes began a propaganda campaign designed to agitate people worldwide and foment hatred against Germans. Within the next two months, after World Jewry broadcast its plans to starve Germany into submission, Hitler had a few things to say about Jewish lies (although unfortunately, people living in countries with a Jewish-controlled press only got to see one side of the story):

"Germany does not want world turmoil or international embroilment. But the national revolutionary Germany has firmly decided to put an end to its domestic mismanagement! Now that the inner enemies of the nation have been rendered harmless by the people themselves, what was long expected has arrived:

The Communist and Marxist criminals and their Jewish intellectual ringleaders, who headed to foreign countries with their monies in time, now unfurl from there an unscrupulous, treasonous hate campaign against all the German people. Since lying has become impossible for them in Germany, they launch it from the capitals of the former Entente, pouring out the same malicious agitations against the young national revolt as they did against Germany at the beginning of WWI.

Lies and slander, steeped in hair-raising perversions, are unleashed against Germany. Gruesome fables of hacked up Jewish corpses, eyes cut out and hacked off hands are distributed with the intention to defame the German people in the world for a second time and in the same way they have accomplished this in 1914. Millions of innocent people, nations with whom the German people only want to live in peace, are agitated against us by these devious criminals.

They want that German goods and German labor fall victim to an international boycott. For them, the poverty in Germany is not severe enough; they want it to be worse!

They lie and tell of Jewish women being killed, Jewish girls being raped before their parents’ eyes, and cemeteries being devastated. All of it is just one big lie, invented with the objective to spawn a new world war hate propaganda! If one were to continue to stand by this maddening crime and do nothing, one would be guilty of accessory!

Therefore, the National Socialist party will now start a defensive campaign against this serious crime with suitable methods to target those responsible. The guilty ones are right here with us. They live among us and abuse day in and day out the hospitality granted to them by the German people.

At a time when millions of us have nothing to live on and nothing to eat, when hundreds of thousands of academics go to waste on the streets, these Jewish scholars are sitting contented among us and claim their guest entitlements. What would the United States do if the German Americans would sin in the same nefarious ways against Americans as these Jews do against Germany? And yet, the National Socialist revolution has scarcely harmed a hair on their head!

They were able to attend to their businesses as before; however, corruption will be eradicated, regardless of who commits it! Belonging to the Jewish race or to the Mosaic religion is as little license for criminal activity as belonging to our race or the Christian faith."

The American Jewish Congress resolved on March 12, 1933, to stage mass protests at Madison Square Garden in New York City, six weeks after Hitler was elected. A week later, the AJC announced that the rally would be held on March 27. The Jewish propaganda apparatus alleged a "campaign of violence" and "brutal treatment being inflicted on German Jewry". Then the Daily Express of March 24, 1933, ran the headline "JUDEA DECLARES WAR ON GERMANY". Thus, the decision to publish that declaration came on - or before - the day of the Enabling Act of March 23, 1933, which allowed Hitler's government to enact laws without the consent of the Reichstag. But Jewry's plan for mass demonstrations was already decided upon before Hitler had gained additional powers, and as shown above, Jews have complained of "massacres", "holocausts", "annihilations", "exterminations" and all manner of persecutions against them since time immemorial.

JudeaDeclaresWar photo JudeaDeclaresWar_zps760b0add.png

Hoaxers argue that the Jews' declaration was merely for an economic war, not a military war. However, Jewry's "holy war" was intended to starve Germany into submission, so that after millions of Germans had lost their lives from malnutrition or disease, the democratically elected nationalist government serving the Germans - and defending the free world against Jewish communism - would collapse and be replaced by another that was simply a puppet of World Jewry and Jewish bankers. (Given that the Jewish Bolshevik Revolution had led to a Civil War that, over the next few years, resulted in two million to 3.5 million deaths merely amongst those fleeing Russia, some three million deaths of starving children, and seven million homeless children, defending against Jewish communism was not to be dismissed lightly.) It was Jews who "drew first blood" with their announcement of a boycott and with their hate propaganda - "the first shot fired in the Second World War" - and then Hitler responded to the provocation with his defensive measures.

So in Hitler's version of events, we have a Jewish propaganda campaign to foment hatred abroad by alleging atrocities perpetrated by Germans against Jews, Jews announcing their boycott and "holy war" against Germans, followed by Hitler's measured response. In Jewry's version of events, the Germans committed terrible atrocities against Jews as soon as Hitler was elected, and then the long-suffering Jews informed the rest of the world and began their campaign for a boycott and a holy war against Germany. International Jewry's 'reality' is already lacking all credibility, given Jewry's standard operating procedure of claiming exterminations and massacres against them. As additional corroboration, we can look at what Hitler actually said on March 28, 1933 in response to the Judea declaration. If Jewry's account were true, Hitler might have been expected to respond with calls for attacks on Jews, to burn their houses down, to rob them, and so on, especially since Hitler had just gained extra powers. But there was not a bit of it in his measured response, which included:

"The action committees are responsible for the utmost protection of all foreigners, regardless of their faith, origin, or race. The boycott is merely a defensive measure exclusively directed toward Jewry in Germany. [...] It must be made clear that the battle against the atrocious Jewish hate propaganda is purely self-defensive. The action committees are responsible that this whole effort proceeds in the most peaceful way and with greatest discipline. Don't even hurt as much as a hair on a Jew's head! We will defeat their provocations simply with the far-reaching impact of these given [economic] measures!"

(Listen to the speech being read in English here by Michael Collins Piper, with comments.)

Perhaps Hoaxers will contend that "Don't even hurt as much as a hair on a Jew's head!" is Hitler's code-speak for "beat them up, burn their houses, poison their dogs". And, since no documented list or written orders concerning such codes was ever found, it was all communicated by "mind reading" and "an incredible meeting of minds"!

In April 1945, Hitler would go on to say:

"It is untrue that I or anyone else in Germany wanted war in 1939. It was wanted and provoked solely by international statesmen either of Jewish origin or working for Jewish interests. I have made too many offers for the limitation and control of armaments, which posterity will not be cowardly enough always to disregard, for responsibility for the outbreak of this war to be placed on me. Nor have I ever wished that, after the appalling First World War, there would ever be a second against either England or America. Centuries will go by, but from the ruins of our towns and monuments the hatred of those ultimately responsible will always grow anew against the people whom we have to thank for all this — international Jewry and its henchmen.

Only three days before the outbreak of the German-Polish war I proposed a solution of the German-Polish problem to the British Ambassador in Berlin— international control as in the case of the Saar. This offer, too, cannot be lied away. It was only rejected because the ruling clique in England wanted war, partly for commercial reasons and partly because it was influenced by the propaganda put out by international Jewry.

I have left no one in doubt that if the people of Europe are once more treated as mere blocks of shares in the hands of these international money and finance conspirators, then the sole responsibility for the massacre must be borne by the true culprits— the Jews."

The New York Times of August 7, 1933 reproduced an address by Samuel Untermyer broadcast on station WABC the previous evening. Untermyer declared a "holy war", a "sacred war", against Germany. Naturally, Untermyer claimed to be fighting for "the cause of humanity" and for "civilization", which of course was turning reality on its head. It was not in the interests of humanity, civilization, or the world's law-abiding people, to fight another world war that would kill tens of millions. Untermyer and his partners-in-crime were fighting on behalf of Jewish communists, Jewish international bankers, Jewish supremacists, Jewish terrorists, Jewry's dream of a "Jewish Utopia", the Rothschild program to turn the world into a giant prison in which the inmates labored under the misconception that they were "free" (and it was just another bizarre coincidence that the world was so messed up), and the orchestration of another world war in which the deaths of tens of millions would create a suitable context for launching a myth about "six million" "exterminated" Jews that would serve to provide the Jewish global crime syndicate with its own sovereign state.

The situation in the run-up to WWII is described by the ex-Jew Ben Freedman, in his 1961 speech at the Willard Hotel in Washington DC.

"Well, in 1933 when Germany refused to surrender, mind you, to the World Conference of Jews in Amsterdam, they broke up and Mr. Untermeyer came back to the United States -- who was the head of the American delegation and the president of the whole conference -- and he went from the steamer to ABC [apparently WABC] and made a radio broadcast throughout the United States in which he said:

"The Jews of the world now declare a Holy War against Germany. We are now engaged in a sacred conflict against the Germans. And we are going to starve them into surrender. We are going to use a world-wide boycott against them, that will destroy them because they are dependent upon their export business."

And it is a fact that two thirds of Germany's food supply had to be imported, and it could only be imported with the proceeds of what they exported. Their labor. So if Germany could not export, two thirds of Germany's population would have to starve. There just was not enough food for more than one third of the population.

Now in this declaration, which I have here, it was printed on page -- a whole page -- in the New York Times on August 7, 1933, Mr. Samuel Untermeyer boldly stated that: “this economic boycott is our means of self-defense. President Roosevelt has advocated its use in the NRA" . [National Recovery Administration] -- which some of you may remember, where everybody was to be boycotted unless they followed the rules laid down by the New Deal, which of course was declared unconstitutional by the Supreme Court at that time.

Nevertheless, the Jews of the world declared a boycott against Germany, and it was so effective that you couldn't find one thing in any store anywhere in the world with the words "made in Germany" on it.

In fact, an executive of the Woolworth Company told me that they had to dump millions of dollars worth of crockery and dishes into the river; that their stores were boycotted. If anyone came in and found a dish marked "made in Germany," they were picketed with signs: "Hitler", "murderer", and so forth, and like -- something like these sit-ins that are taking place in the South.

R. H. Macy, which is controlled by a family called Strauss who also happen to be Jews. . . a woman found stockings there which came from Chemnitz, marked "made in Germany". Well, they were cotton stockings. They may have been there 20 years, because since I've been observing women's legs in the last twenty years, I haven't seen a pair with cotton stockings on them. So Macy, I saw Macy's boycotted, with hundreds of people walking around with signs [saying] "MURDERERS" and "HITLERITES", and so forth.

Now up to that time, not one hair [on the head] of any Jew had been hurt in Germany. There was no suffering, there was no starvation, there was no murder, there was nothing.

Now, that. . . naturally, the Germans said, "Why, who are these people to declare a boycott against us and throw all our people out of work, and our industries come to a standstill? Who are they to do that to us?" They naturally resented it. Certainly they painted swastikas on stores owned by Jews.

Why should a German go in and give their money to a storekeeper who was part of a boycott who was going to starve Germany into surrender into the Jews of the world, who were going to dictate who their premier or chancellor was to be? Well, it was ridiculous.

That continued for some time, and it wasn't until 1938, when a young Jew from Poland walked into the German embassy in Paris and shot one of the officials that the Germans really started to get rough with the Jews in Germany. And you found them then breaking windows and having street fights and so forth.

Now, for anyone to say that -- I don't like to use the word 'anti-Semitism' because it's meaningless, but it means something to you still, so I'll have to use it -- the only reason that there was any feeling in Germany against Jews was that they were responsible: number one, for World War One; number two, for this world-wide boycott, and number three -- did I say for World War One, they were responsible? For the boycott -- and also for World War II, because after this thing got out of hand, it was absolutely necessary for the Jews and Germany to lock horns in a war to see which one was going to survive.

In the meanwhile, I had lived in Germany, and I knew that the Germans had decided Europe is going to be Christian or Communist: there is no in between. It's going to be Christian or it's going to be Communist. And the Germans decided: "We're going to keep it Christian if possible". And they started to re-arm.

And their intention was -- by that time the United States had recognized the Soviet Union, which they did in November, 1933 -- the Soviet Union was becoming very powerful, and Germany realized: "Well, our turn is going to come soon, unless we are strong." The same as we in this country are saying today, "Our turn is going to come soon, unless we are strong."

And our government is spending 83 or 84 billion dollars of your money for defense, they say. Defense against whom? Defense against 40,000 little Jews in Moscow that took over Russia, and then, in their devious ways, took over control of many other governments of the world."

The physical impossibility of the extermination "gas chambers" legend

Now we come to the physical impossibility of the extermination gas chambers narrative, and how the various lines of evidence converge on the fact that there were no extermination gas chambers and there was no extermination policy. After Hoaxers abandoned their claim of "four million" killed at Auschwitz, admitting it was simply Soviet propaganda, the latest allegations range from "Between 1.3-1.5 million people were murdered in the gas chambers of Auschwitz -- more than 90% were Jews" to "1,100,000 Jews and 200,000 others". So let's take the lesser claim of 1.3 million murdered.

We'll start with the known facts about the available coke at Auschwitz, the empirical evidence showing that it is not possible to cremate bodies with a kilogram or two of coke, and then look at how the law of conservation of energy precludes any possibility of cremating bodies with negligible fuel. Indeed, in the exterminationist thesis, if the Sonderkommando had made such a blunder as to attempt cremations with tiny amounts of coke such that the bodies remained unburned hours later when the next batch of bodies was dragged up from the gas chambers, there is no doubt that the hapless Sonderkommando would have been either summarily shot or selected for the next group destined for gassing. After they had been made an example of, the survivors would impress upon newcomers the importance of using sufficient coke.

Coke availability at Auschwitz-Birkenau

The coke deliveries to Auschwitz from February 1942 to October 1943 are fully documented, and amounted to 1,037 tonnes, an average of around 50 tonnes per month, as admitted by the Hoaxer Jean-Claude Pressac. 50 tonnes per month extrapolated over three years of the alleged "extermination" policy is 1,800 tonnes. Thus, 1,800,000 kg of coke divided by 1,300,000 bodies needing cremation is ~1.4 kg of coke available per body. As we shall see, this compares with a minimum requirement of 14 - 28 kg of coke to cremate a body, and a requirement of 4.3 kg of coke (129 MJ) merely to boil the water in the average corpse and heat the vapor to the exiting gas temperature, before even beginning to count having to heat the combustion air, denature the proteins, calcinate, shrink, delaminate and fracture the bones, the initial heating of the firebricks, and losses from heat that is vented out with the other exhaust gases.

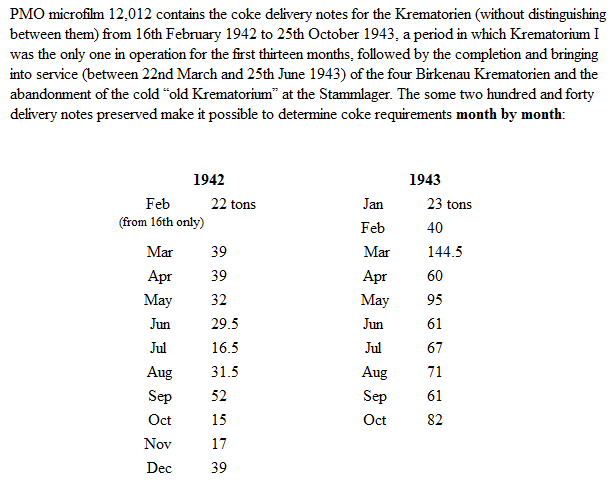
PressacCokeDeliveries photo PressacCokeDeliveries_zpscd2d6249.png

Source: AUSCHWITZ: Technique and Operation of the Gas Chambers [p. 224] - Jean-Claude Pressac

Also see the rather neater table provided by Germar Rudolf in Lectures on the Holocaust, which shows how the monthly deliveries averaged 30 tonnes until the end of February 1943, and then the March to October average is 80 tonnes per month. The March figure is very large, and Pressac claimed it served for drying and preheating the new Birkenau ovens. Crematoria II to V all went into operation between March and June 1943. In fact, as Carlo Mattogno shows in Auschwitz: The Case for Sanity [p. 333], the drying was essentially carried out with wood, and the requirement to heat all of the ovens - ten triple-muffles and two 8-muffles - was only around 6% of the coke supplied in March 1943.

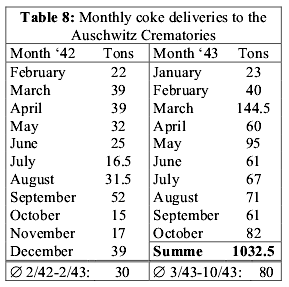
AuschwitzCokeDeliveries photo AuschwitzCokeDeliveries_zps18ff8bbc.png

Source: Lectures on the Holocaust [p. 223, 2005 edition] - Germar Rudolf

[Note: the 1,032.5 should read 1,037 tons.]

If we took Pressac's word, we should exclude the March 1943 figure as a one-off, leaving the April to October 1943 average at 71 tonnes per month. However, to be as accommodating as possible to the exterminationist thesis, let's use the 80 tonnes per month March to October average to extrapolate for the following 13 months, November 1943 to November 1944. Towards the end of 1944 the intensive Allied bombing of supply lines, resulting in many deaths from malnutrition and typhus owing to a lack of food and medicines, would hardly have helped in allowing coke deliveries. Krema II and III stopped operating November 27, 1944; Krema IV stopped October 7, 1944, and Krema V stopped January 18, 1945 (see Auschwitz: The Case for Sanity [p. 291]). So we can take the end of November as the average date for ceasing cremations. Hoaxers generally claim an extermination policy began in 1942; we'll say the middle of January. The delivery figures start from February 16, 1942, so we'll add an extra 30 tonnes there, and an extra 80 tonnes per month for 13 months. Thus, the total coke available becomes 1,037 + 30 + 80 * 13 = 2,107 tonnes.

And so 2,107,000 kg of coke divided by 1,300,000 bodies is ~1.6 kg of coke per body.

Coke requirement at Auschwitz-Birkenau, if Hoaxers' allegations were true

In Dissecting the Holocaust, in the chapter "The Crematoria Ovens of Auschwitz and Birkenau" [5.2 to 5.3] by Carlo Mattogno, he shows the results of his heat balance calculations for the "minimal theoretical coke consumption per corpse". Also see his 2010 work, Auschwitz: The Case for Sanity,[8.5.2 to 8.5.4], e.g., as in the table below.

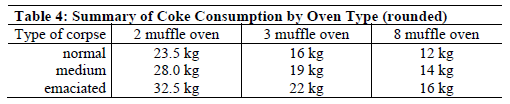
TopfCokeConsumptionMinimum photo TopfCokeConsumptionMinimum_zps0f4c42fa.png

Source: Auschwitz: The Case for Sanity [p. 271] - Carlo Mattogno

As might be expected, the three-muffle provides a saving in coke consumption over the double-muffle, and the eight-muffle provides further economy compared to the three-muffle ovens. Similarly, the "normal" body, with its greater fat content, required less coke than the "medium" (moderately skinny) body, and the "emaciated" body ("Muselmann") required the most coke. Since even Hoaxers admit that some prisoners were emaciated or "Muselmann", and starvation sickness led to a number of deaths, and there certainly wasn't enough food available to classify the average corpse as a "normal" body, we can take the "medium" or moderately skinny body as the average. Mattogno found that the eight-muffle oven's minimum coke requirement was 14 kg of coke for the moderately skinny body, 11.75 kg (or ~12 kg) of coke for the normal body, and 16.25 kg (or ~16 kg) of coke for the emaciated body. For the three-muffle oven, the corresponding figures were 19 kg, 16 kg and 22 kg.

Those calculations were not simply speculation; they were based upon solid data from 1941 ["The Crematoria Ovens of Auschwitz and Birkenau", 8.5.1] showing that the Topf double-muffle oven at Gusen required 20,700 kg of coke to cremate 677 corpses, an average coke consumption of 30.6 kg per body.

Thus, even if we are very generous to Hoaxers, and pretend all ovens achieved the theoretical minimum coke consumption of the eight-muffle oven, then the moderately skinny body requires 14 kg of coke per body, compared with the 1.6 kg of coke per body that was available. In fact, as calculated below, given the numbers of each type of oven, the average works out at around 18.5 kg of coke per corpse. It can be seen that the chasm between reality and Hoaxer fantasy land is at least one order of magnitude. This is even after Hoaxers reduced their preposterous claim of "four million" killed at Auschwitz by a factor of three; the coke requirement is still around ten times higher than the coke available!

Corroborating evidence of ~150,000 as the maximum Auschwitz death toll

Forgetting the Hoaxers' fantasy world for the moment, those of us who prefer to dwell in reality will be interested to know how many bodies could have been cremated, given the coke available. 2,102,500 kg of coke divided by 14 kg of coke per body is 150,178 bodies.

Another line of evidence concerns the lifespan of the ovens' firebricks [ibid. 9.0]. The Topf firm had managed to extend the lifespan of the firebricks from 2,000 to 3,000 cremations. There is no evidence that any of the 46 muffles at Birkenau ever had any brickwork replaced, which places their maximum capacity at 46 x 3,000 = 138,000 cremations. There are records indicating that firebricks were replaced at one double-muffle oven at Auschwitz I, so the total capacity for its three double-muffle ovens is (6 + 2) x 3,000 = 24,000. Thus, 138,000 plus 24,000 is a maximum nominal capacity of 162,000 bodies.

As Mattogno says, if the brickwork of the muffles had been replaced five times, an immense number of documents would have been generated. But there is no trace of that in the extensive correspondence between Topf and the SS Construction Office. (And that's just assuming Pressac's lower figure of an extra 530,000 gassing victims; the 1.3 million claim would need about twice as many replacements.) Another case of evidence being "destroyed"?? Or were the Germans so devious that they communicated by "telepathy"- both to circulate orders and instructions for an "extermination" program, and also for more routine matters such as maintenance of the crematoria??

The death books already mentioned is another line of evidence. There was the lower estimate of "almost 69,000" deaths of registered prisoners "who died between July 29, 1941 and December 31, 1943", which would suggest a total figure including 1944 of around 100,000. Then, for a higher estimate, which assumes additional deceased female inmates being recorded separately in undiscovered registers, there is Mattogno's figure of 160,000 to 170,000 deceased registered inmates at Auschwitz and Birkenau.

Some sources quote as long as three hours for the cremation process; others state "between 1 1/2 – 2 hours". That doesn't include the twenty minutes required for grinding the remaining bone fragments into fine ashes, although that could be done as the next body was being consumed. The cremation time of modern cremators such as the "Joule" or the "Newton" is given as 70 minutes. In the 1998 study by M. Bohnert et al, the duration of the cremation within the first cremation chamber was 50 to 80 minutes. This was the time at which the torso broke apart.

Each Auschwitz cremation oven was in existence for about 600 days. They could not be run 24/7, and there was a significant proportion of downtime for repairs and maintenance. Let's be generous and suppose the Topf ovens could beat modern cremators and achieve 60 minutes per body. If we say 12 hours per day after allowing for downtime, then that's 52 muffles at 12 cremations per day for 600 days, and so the maximum capacity is 52 x 12 x 600 = 374,400 bodies. Again, even this is well short of 1.3 million, but the capacity does allow for the actual number of deaths from natural causes, after we abandon Hoaxer fantasyland and come back down to reality.

In order to cremate 1.3 million corpses at 60 minutes per corpse, the ovens would have had to have been running for 1,300,000 / (52 x 600) = 42 (forty-two) hours per day.

(See Mattogno "The Crematoria Ovens of Auschwitz and Birkenau" [7.4 to 8, which, in more detailed calculations, concludes a theoretical maximum of 312,700 alleged gassed victims that could have been cremated, plus tens of thousands who died from natural causes. That's if we forget the fact that the firebricks could not take it, and the fact that there was not enough coke.)

These lines of evidence converge on a death toll between 100,000 and 170,000, which is consistent with natural deaths from disease and malnutrition in the wartime early 1940s, aggravated by Allied bombing of supply lines, and is clearly not consistent with the extermination program thesis. Also inconsistent with an extermination program is the absence of stable cyanides in the walls of the alleged "gas chambers", the absence of holes in the roof of the alleged "gas chambers", the absence of written orders or a budget or a plan for an extermination program, the absence of a single autopsy confirming a death from gassing, the absence of a single photograph or any film footage showing a gas chamber, the fact that more than 90% of Hoaxers' claims are already accepted as lies, and the fact that Hoaxers have had to resort to obtaining confessions through torture, forging 'documents', murdering the revisionist François Duprat by blowing up his car, sending a lethal pipe bomb to Ernst Zundel's home, beating up Professor Faurisson at least ten times including breaking his jaw, enacting laws to have revisionists detained, extradited to another continent and jailed for years merely for stating their opinions, and employing a pretty young redhead to pretend to confuse a porcelain factory's pierced mullet star brand mark with a Star of David and to pretend to think that the discovery of 40 bone fragments in a cemetery is evidence that nearly a million were murdered at an extermination camp.

The claim of multiple, simultaneous cremations per muffle - some preliminary notes

Hoaxers will jump through all kinds of hoops in their desperation to pretend that their assertions are not refuted by the known laws of physics, chemistry and mathematics. These range from claims that a greater efficiency could be achieved by stuffing multiple bodies into a single muffle, to claims that bodies can burn by themselves with negligible fuel.

In the Irving vs. Lipstadt trial, for example, Lipstadt's lawyer Richard Rampton claimed "...you can incinerate up to four corpses at a time in any one muffle. Do you know why you do that, Mr Irving? Because they self-combust. You mix fat corpses with thin corpses and then you do not need much coke supply; it keeps going under its own steam?"

That is a demonstrably false statement, albeit one that has been so frequently repeated by Hoaxers that some people come to imagine it as 'fact'. Irving cited a pretty reasonable estimate: "It takes 30 kilograms of coke to burn one body, whatever Mr Rampton is about to say now." That's not far off the 28 kg of coke per "moderately thin corpse" that Mattogno states in "The Crematoria Ovens of Auschwitz and Birkenau" [5.2] for the Topf double-muffle cremation - and then the triple-muffle goes down to 19 kg and the eight-muffle down to 14 kg. And those figures are all theoretical minimums, unachievable in practice.

But the idea that further gains in efficiency, fuel economy or combustion time can be achieved by simultaneous cremation of multiple bodies in each muffle is simply wrong. The Topf ovens at Auschwitz-Birkenau were designed for one corpse per muffle. In the three-muffle oven, combustion gases entered through four rectangular openings along the apex line of the chamber vault and flowed from top to bottom (see Auschwitz: The Case for Sanity [pp. 257-261], Carlo Mattogno). There were also four rectangular openings in the sidewalls of the outer muffles. The spent gases from the outer muffles had to flow into the central muffle through three large rectangular openings in the sidewalls that linked the central muffle to the outer two, down past the central corpse and into the post-combustion chamber, whereupon the spent gases exited via two large rectangular discharge openings in the sidewalls of the post-combustion chamber. A gasifier fed each outer muffle, and the corpse in the inner muffle was merely heated indirectly by the combustion products that had already been employed to heat the walls and corpses in the outer muffles.

The eight-muffle oven (ibid., pp. 262-5) was arranged with four gasifiers in the center, two by two. On each side of the gasifier central block were four muffles, again, two by two. If we imagine each group of four as one pair adjacent to the gasifiers and another pair on the outside (the lateral pair), then each pair shared the two inner walls between its muffles. If we imagine each pair as one adjacent to the gasifier and one on the outside, each pair shared its two rear walls with the pair opposite. It's in this latter way that the muffles were configured as four pairs of linked muffles; the combustion products from the gasifier entered the adjacent muffle, flowed from one side of the muffle to the other, through openings into the lateral muffle, from one side to the other, and the spent gases were discharged into an outlet that opened into a vertical duct towards the rear of the outer wall of the lateral muffle. The combustion air for the corpses entered via an air channel with a large hinged door next to the muffle gate, and through another channel with a standard sized door next to the ash chamber door; each gasifier hearth also had a standard sized door. Similarly to the three-muffle, the corpse in the final muffle was heated indirectly by combustion products that had already been used in the preceding muffle. Whereas the triple-muffle had two gasifiers serving three muffles, the eight-muffle had one gasifier for every two muffles. (In the eight-muffle, the central part with the four gasifiers, two wide, had a total width of 2.29 m. The height was 2.45 m; the width of a pair of muffles was 2.545 m, and the total depth, a little more than the length of two muffles, was 4.43 m. So the eight-muffle installation was 2.45 m high with a floor area of 4.43 m deep by [2.29 + (2 x 2.545)] = 7.38 m wide.)

Thus, for the three-muffle, it was necessary for gases in the central muffle to flow vertically down past the corpse, into the post-combustion chamber and out through the discharge openings. In the outer muffles, it was essential that the gases could flow into the central muffle via openings set into in the sidewalls. And the gasifier neck opened into the rear wall of the muffle, requiring a back to front and an outer to central muffle flow. The eight-muffle required that the gases flowed from one side of the muffle to the other, in both the inner and outer muffle. Multiple corpses per muffle would block the openings between center and outer muffles in the three-muffle, and between inner and lateral muffle in the eight-muffle, obstructing the flow of combustion gases. What's more, by reducing the effective cross-section of the muffle, the gas that does manage to flow past is forced to speed up just as a river must speed up at the shallower or narrower sections; the residence time of the gas in the muffle is reduced, there is less time for the gas to transfer its heat to the corpse, more heat is wasted in the heat of the smoke, and the firebricks in the flue and chimney are damaged by the excess heat.

And as the bodies are stacked up together, the ratio of the absorbing target area to the target mass decreases, as part of each corpse is shielded by the other. Most of the heat transferred to the corpse is by radiation, and the rate at which it is absorbed is directly proportional to the surface area of the corpse. To look at some examples, the double-muffle was 700 mm (height) by 700 mm (width) by 2,000 mm (height), and the three-muffle was 800 mm (height) by 700 mm (width) by 2,000 mm (length), plus the inclined, v-shaped post-combustion chamber, of which the front portion constituted the ash chamber. The corpse was placed on the five transverse bars of refractory material on the partly open floor, above the post-combustion chamber (ibid., pp. 255, 259, & 263-48).

The average adult human body has a surface area of 1.8 m². Alternatively, viewed from the front or rear, the cross-section viewed could be considered to approximate a rectangle of 1.7 m x 0.35 m, which is ~0.6 m². Thus, the area seen from the front and the back comprises two-thirds of the total, and the remaining third is made up by the sides and everything else. In the cremation, the body is mainly heated by absorbing infra-red radiation that is emitted mostly from the refractory walls, and partly from the flowing gaseous combustion products. Most of the points in the combustion chamber are looking down on the 0.6 m² front view of the corpse. Ideally, for maximum absorption, the corpse would be spherical, and suspended in the middle of the chamber.

So when a second corpse is stacked on top of the first, the surface area of the absorbing target - as seen by most of the points that are emitting radiant heat - has increased only very slightly. There is still the 0.6 m² front or rear view, and for the minority of emitting points at the bottom of the walls, the side area has doubled. For other points, the side has increased, but they're seeing it at an angle and it's a small increase. The minority of points that are at the bottom still see the lower side. Even if we decide to disregard the fact that most emitting points are above the corpse and instead give equal weighting to the whole surface area, we still have a top and bottom area each of 0.6 m², and now the side view has doubled in area. So in total, it's up about one-third, from 1.8 to 2.4 m². It certainly hasn't doubled to 3.6 m², but at the same time the mass has doubled from 55 to 110 kg, and so the energy required to heat the remains has doubled. (This is covered in more detail below.)

If they tried to fit two corpses side by side, the gases in the three-muffle's center muffle would be severely obstructed from flowing down into the ash chamber and the flue duct, and for the three- and eight-muffle, openings in the sidewalls would be severely blocked. Since the loading devices were designed for introduction of a single corpse, multiple corpses would raise the question of how additional corpses could be loaded into the hot furnace without the operators being seriously burned, and the increased loading time would increase heat losses through radiation when the muffle gate was open.

Since the 'evil Nazis' are not supposed to have used coffins in their dastardly extermination program, there would have been a considerable drop in oven temperature during the initial phase of the cremation cycle in which the corpse's water evaporates. Using multiple corpses per muffle would increase the amount of this temperature drop, increasing the likelihood that the temperature would fall below 600 °C, in which case the body would merely carbonize rather than cremate, and the Sonderkommando would be facing the bullet or the gas chamber. In the event that the ovens were already so hot that the cremations succeeded, then as the corpses were into the fat burning phase, the peak in temperature of exhaust gases would damage the refractory lining of the flue and chimney. Moreover, with greater temperature fluctuations, the firebricks in the ovens would not even have lasted for 3,000 cremations, let alone the minimum of 25,000 (1.3 million bodies / 52 muffles) that exterminationists require to make their conspiracy theory work.

Hoaxers will frequently claim to have some "document" that 'proves' their case. Naturally, they give a wide berth to the science, logic, feasibility and physical evidence. "Documents" can be forged; the laws of science cannot be suspended every time an enemy of World Jewry is supposedly involved in some diabolical "conspiracy", whether it's "Arab" hijackers with box cutters who helpfully manage to take down three steel-framed high-rises in terrorist attacks six weeks after a Jewish businessman insured for billions of dollars against terrorist attacks, leaving what the chief structural engineer responsible for designing the building described as "a little river of steel, flowing" in the debris pile, after "office fires" that don't go above 1,200 °C turned fireproofing into a "glassy residue" when the fireproofing is known not to undergo any phase changes until well over 1,200 °C, or it's Germans bent on a fiendish plan to take over the world and "exterminate" the Jews in "gas chambers" using only a thousandth the cyanide levels that they were simultaneously using in delousing chambers to save Jews' lives, and then get rid of the evidence by temporarily intersecting with a parallel world in which bodies are self-combusting. "Documents" are no more credible than statements by Benjamin Netanyahu or Elie Wiesel.

Mattogno provides data from animal carcass incinerations, in which several whole bodies or parts of them were cremated simultaneously in the same oven.

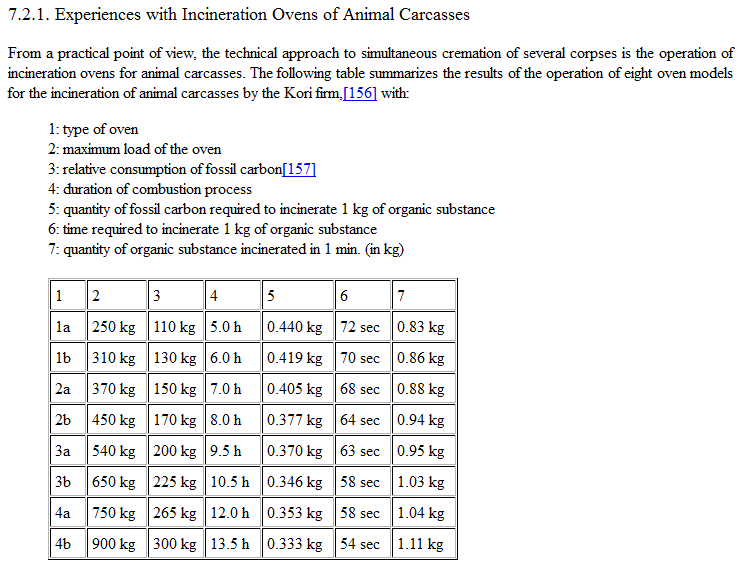
KoriAnimalCremations photo KoriAnimalCremations_zps5c97a4dc.png

Source: Dissecting the Holocaust, "The Crematoria Ovens of Auschwitz and Birkenau" [7.2.1], Carlo Mattogno

Those Kori ovens were specially designed for the mass incineration of animal carcasses, and note how even with the largest model "4b", it still requires 0.333 kg of fossil carbon for each kg of organic substance incinerated. 900 kg is equivalent to many times more than four people, especially underfed concentration camp inmates! In 2005, the average weight of Europeans was 70.8 kg (156 lb); Asians were the lightest at 57.7 kg (127 lb). One source says the average adult, when Auschwitz was liberated, was 35 kg (77 lb). Even if we assume this as an average body weight, and take the largest oven above, it would still requite 0.333 * 35 kg = 11.65 kg of fossil carbon per body.

(The figures in the table are for pure carbon, which, in the reaction C + O₂ ==> CO₂, the heat released is 32.76 MJ/kg of carbon. Coke is not pure carbon, and yields 28-31 MJ/kg, so the coke requirement is about 10% higher than the carbon required, and the 11.65 kg of fossil carbon becomes 12.8 kg of coke.)

There are several reasons why cremations at Auschwitz required more than 12.8 kg of coke per body. Firstly, throughout the Auschwitz camp's existence, the average inmate was not as emaciated as the survivors when the camp was "liberated", following the breakdown of supplies in the final months. Thus, the average weight would have been more than 35 kg. Secondly, the animals in the tests would not have been as skinny as the average Auschwitz inmate even under the camp's normal operating conditions, and so with more fat, would have needed less fuel. Thirdly, unlike the Kori ovens, the Topf ovens were not designed for multiple charges, and so would have needed more time and fuel for any given load. Fourthly, the oven model 2b in the above table, which is not quite as efficient as 4b, had a muffle with a surface area of 1.38 m² that was almost equal to the 1.4 m² of the Topf triple-muffle oven.

Mattogno assumes 40 kg for an emaciated corpse, 55 kg for a moderately thin corpse, and 70 kg for a normal corpse, so his example of a moderately thin corpse of 55 kg needing 14 kg of coke in an eight-muffle Topf oven has 0.25 kg of coke per kg of organic substance incinerated. The corresponding moderately thin corpse in the three-muffle is 19 kg of coke for a 55 kg body, so is 0.345 kg of coke per kg of organic substance incinerated. Then the same 55 kg corpse in the double-muffle requires 28 kg of coke, so is 0.51 kg of coke per kg of organic substance. So the coke requirement per kg incinerated remains approximately in the range 0.25 to 0.5 kg per kg, depending on the efficiency of the oven.

So, at minimum, some 14 kg of coke is required per body - even in the most efficient eight-muffle Topf oven, and stuffing several bodies in the same muffle would not have provided any advantage, either in fuel economy or in time required to incinerate a body. Now we come to Hoaxers' other scheme for making bodies "self-combust", as when Rampton said, "You mix fat corpses with thin corpses and then you do not need much coke supply; it keeps going under its own steam." Here again are the figures calculated by Mattogno for the heat balance of the various Topf ovens, depending on the type of corpse:

TopfCokeConsumptionMinimum photo TopfCokeConsumptionMinimum_zps0f4c42fa.png

Source: Auschwitz: The Case for Sanity [p. 271] - Carlo Mattogno

The saving in fuel consumption from cremating the "normal" body, as opposed to the "emaciated" body is already reflected in the reduction from 16 to 12 kg, a 25% reduction, in the case of the eight-muffle oven. (The saving for the "normal" body is around 28% with the double-muffle, so still roughly the same percentage.) Now, suppose you were going to cremate an emaciated body together with a normal body. The energy released from the normal body's fat has already been expended in helping to cremate that body with a lower amount of coke. It can't come back and have a "second go" with another body; that would be tantamount to a perpetual motion machine and is a violation of the law of conservation of energy. The Hoaxers' argument is like claiming that if you have 2,257 kJ of energy available, you can use that to vaporize a liter (kg) of water that's already preheated to 100 °C, and then use the same energy again to vaporize a second liter of water that's already preheated to 100 °C. And once you can "reuse" energy a second time, why not a third time, or a millionth time? James Joule would be turning in his grave!!!

In addition, the advantage from burning the fat will accrue irrespective of the number of bodies in the oven.

So the total coke consumption expected for an emaciated body together with a normal body will not be any lower than 16.25 + 11.75 kg = 28 kg, the same as two of the moderately thin bodies. Moreover, that 28 kg is too low in this case, since it doesn't allow for the fact that the Topf muffles weren't designed for multiple charges. As described above, there would be a loss in efficiency from the increase in gas velocity and from the shielding effect of having bodies stacked together, such that each body is absorbing heat over a smaller fraction of its surface area.

Time and fuel requirements in the cremation process - thermal barriers

The 14 kg per body would not be achievable overall, since it exceeds that available from the less efficient three-muffles and double-muffles, and assumes a preheated oven that runs continuously. The ovens had to stop three or four hours a day, during which time they would cool, and they had to stop for longer periods of maintenance, after which they would have to start up from cold. Of the 52 muffles in total at Auschwitz-Birkenau, the three double-muffles at the crematorium of Auschwitz I accounted for six, the ten three-muffles in the crematoria II and III of Birkenau accounted for thirty, and the two eight-muffle ovens in the crematoria IV and V of Birkenau accounted for sixteen. Thus, for the moderately thin body, the coke consumption from all 52 muffles averages out at (6 * 28 kg + 30 * 19 kg + 16 * 14 kg) / 52 = 18.5 kg per body as a theoretical minimum. Nevertheless, the 14 kg figure is useful to take as a most optimistic benchmark to compare with the 1.6 kg per body that Hoaxers require.

Another reason why bodies cannot "self-combust" is that the fat burns over a fairly narrow proportion of the total cremation time of 60 minutes or more. First the body is dried out, and then the fat burns in the first 10 or 15 minutes. Some of the energy released has helped in the early stages of the cremation (and a recuperator can amplify this advantage by minimising the proportion that is rapidly convected out with the hot exhaust gases and lost to the environment. Then, throughout the larger, secondary phase of the cremation cycle, an energy source is still required to break down the proteins and the rest of the tissue, as the bones go through the stages of decomposition, inversion and fusion. This is one reason why the fat of the normal body can only provide a fuel saving of some 27-28% compared to the emaciated body.

Although cremations in peacetime consume a great deal of energy, it would be even more if it weren't for the contribution by the coffin. For example, 200 lb of wood, say 90 kg, at 19 MJ/kg provides 90 * 19 MJ = 1,710 MJ, equivalent to the energy released from burning 57 kg of coke. However, as with the fat, the actual saving in fuel is much less than that, because the coffin is consumed early in the cremation cycle, after which the fuel must continue to provide the required energy.

The following papers referred to (Swain, 1952, and Jones & Williamson, 1975) are available from The Cremation Society of Great Britain (go to "Legal and Research", then select "Index of past Cremation Conference papers and order form"). These people from the cremations industry can hardly be dismissed as "neo-Nazis" or "anti-Semites".

The 1952 presentation by J.A. Swain shows how, even if we suppose a cremation time of only one hour, the cremation cycle's primary phase - in which burning fat makes a significant contribution - lasts for less than a quarter of the cycle. Heat must be applied initially to dry out the charge and ignite any fats, and the primary phase is concluded after the first ten or fifteen minutes.

New Developments in Cremation Furnace Design - J.A. Swain (1952)

J.A. Swain (Sales Manager, The Incandescent Heat Co. Ltd., Smethwick [West Midlands, UK]): "[...] A further point became apparent - that in the initial stages of the application of heat an enormous volume of combustible material was converted to gas, which if thoroughly oxidised, gave a very high heat release which would leave the system without doing effective work. Further, that after the first few minutes, say ten, twelve or fifteen minutes, the process then reverted to the oxidation of residual carbon, and calcination, and that during this latter phase ample heat would be required to heat the air containing 21 per cent oxygen to the appropriate high temperatures necessary to complete the oxidation process - during the secondary phase, very little, if any, supporting heat from the charge itself would be available, all or most of the heat having been given off in the first ten or fifteen minutes of the cycle.
Recuperators are applied to some cremators working reasonably well during the active burning of the charge when the products of combustion are flowing through them, and hot air is produced by counter flow currents. Highly preheated air is less necessary in this phase than in the secondary phase when there is very little in the way of combustible products except residues and consequently the recuperator cools down very rapidly and fails to give the required flow of highly preheated air at the time when it is most necessary.
It was concluded therefore that the only real advancement which could be made was to design a special form of duplex regenerator of the rapidly reversing type having the following functions.

To collect and store the heat from the outgoing gases and on reversal return this heat in the form of highly preheated uncontaminated air, with the highest oxygen content.

To perform the useful purpose of heating the installation as rapidly as possible from cold to starting temperature of about 650 °C.

To have sufficient thermal capacity to absorb most of the heat of oxidation in the initial period of heating when the gasification is most vigorous, and to effect thermal storage of this heat - which is ordinarily thrown away by discharge to atmosphere - and return this heat during the later phase of the cycle to effect the final oxidation of carbon residues and complete the process of calcination in the minimum of time."

Swain says the tests were not carried out with human remains, but "The animal remains that have been placed in an ordinary coffin for all tests carried out have been equivalent - as far as we could get - to the ten stone [63 kg] human being." One questioner asks if the charge was a "whole body", and points out: "If it was not a whole body, and if it was a load of pieces of animal flesh the pieces would have more surface and that would assist in the oxidation of the charge." Swain replies: "Being quite ignorant of the actual process of cremation, we felt it would be better to bring in experts, as we have in all our consultations. The charges delivered to us have been made up by experts in the cremation industry and by funeral directors who have delivered to us something which they tell us is the equivalent of a human body, as they know it, for scientific use."

He claims a time of 35 minutes, but when pressed on that says, "In reply to the last question, the 35 minutes is not the complete cycle. Thirty-five minutes is the time taken for the primary cycle, after which there may be 10 minutes or 15 minutes for the final calcination of the small quantity that remains. The virtue of the system developed is that as long as your primary cycle is complete, another charge can be placed into the chamber without there being the slightest possibility that there is any contamination from the previous charge. There are entirely separate chambers which complete the final calcination, but using very little heat instead of having additional heat for that purpose."

The Swain presentation demonstrates how the manufacturers' representatives can sometimes be a little over-ambitious in describing the performance of their products. Topf engineers Kurt Prüfer and Karl Schultze were interrogated by the Soviets in 1946 (another reason to exaggerate their claims). From "The Crematoria Ovens of Auschwitz and Birkenau" [6.6] - Carlo Mattogno:

During the interrogation on March 4, 1946, K. Schultz stated:[148]

"Five ovens were in two crematoria, and three corpses were introduced in each oven [one in each muffle], i.e., there were three openings (muffles) in each oven. In one crematorium with five ovens [and fifteen muffles], one could incinerate fifteen corpses in one hour."

During the interrogation on March 5, 1946, K. Prüfer explained why the cremation lasted so long in the Birkenau crematoria:[149]

"In civil crematoria, pre-heated air is blown in with the help of special bellows, due to which the corpse burns faster and without smoke. The construction of the crematoria for the concentration camps is different; it was not possible to pre-heat the air, as a result of which the corpse burned slower and with developing smoke. In order to reduce the smoke and the smell of a burning corpse, a fan is used.

Question: How many corpses would be cremated per hour in a crematorium in Auschwitz?

Answer: In a crematorium that had five ovens and fifteen muffles, one cremated fifteen corpses in an hour."

Nevertheless, if we suppose that they weren't exaggerating and the ovens could manage one corpse per hour per muffle, then that would still allow only 374,400 bodies as calculated above. Note how the oven design has nothing fancy such as preheated air. If the Germans had really been "exterminating" Jews on an industrial scale, they'd have built massive industrial incinerators; they wouldn't have been using ovens designed for single charges like the Topf ovens. And they wouldn't have built gas chambers with doors that opened inwards, with the handles on the inside. ("Achtung! You filthy swine, open that door, schnell!" "Duh! They can't; they're dead. Order a battering ram from Berlin.") And they wouldn't have chosen to build "gas chambers" in a cellar (although of course that's the ideal place for a mortuary to keep the bodies cool in summer), such that it was necessary for the smoking, eating, and/or gas mask wearing forced laborers to go into the cyanide-contaminated chamber to haul the bodies back up to ground level to incinerate them. (How often do you see people smoking whilst going into a cellar contaminated by explosive cyanide gas? Ever seen anyone eating or smoking whilst wearing a gas mask?) And they wouldn't have been using 99.9% of their Zyklon B in delousing chambers to save their prisoners' lives. But since when has logic or common sense ever featured in Hoaxer dreamland?

Moreover, Hartmut Topf revealed that his relatives were not "anti-Semites" or "evil Nazis", and "faced no personal risk for declining orders for furnaces from Hitler's elite SS guards", which makes a mockery of the idea that Topf engineers colluded in a program for the "extermination" of the Jews.

In a hypothetical extermination program, as Hoaxers will love to point out, the Germans would have no need to worry about "contamination from the previous charge". However, a) The Topf ovens didn't have Swain's "special form of duplex regenerator of the rapidly reversing type"; they didn't even have preheated air. b) Either the "special form of duplex regenerator of the rapidly reversing type" never took off, or if it did, it did not manage to reduce times to less than an hour, as seen by the fact that modern cremators take more than an hour to incinerate a human body, and by the fact that 60 minutes was still seen as an insurmountable barrier in subsequent discussions at the same The Cremation Society of Great Britain conferences, twenty-three years later in 1975. The following paper also explains why cremations come up against this thermal barrier and the minimum time of around 60 minutes per body.

Now, if the Germans had been using some "atomic" "weapon of destruction", they would have been able to blast 20,000 Jews into the twilight zone in very little time, but then Hoaxers are faced with a very different set of problems. Alternatively, if they had some furnace capable of generating temperatures of 2,000 °C, they might have got their cremation times under an hour per muffle per body, although a higher coke consumption per body would be inevitable. The Topf ovens, of course, came nowhere near such temperatures, and if they had, the firebricks would almost certainly have melted, were not designed to handle such temperatures, and would not have achieved even 3,000 cremations per muffle and 162,000 bodies in total. Also, as Mattogno points out in "The Crematoria Ovens of Auschwitz and Birkenau" [3.6], "At temperatures of over 1100 to 1200° C (2010 to 2190° F) one encounters the phenomenon of sintering, where the bones of the corpse and the oven refractory begin to soften and to melt together (fuse)".

The Hoaxers' extermination conspiracy theory is impossible on technological grounds (durability of firebricks), on chronological grounds (too long to cremate each body) and on fuel consumption grounds, and if they try to solve one of their fatal problems, the others become even more intractable.

Factors Which Affect the Process of Cremation - Dr. E.W. Jones & Mr. R.G. Williamson (1975)

Dr. Jones: "[...] Out of the original ten factors, that as a team we had sat down and noted, and apart from the ones that we had agreed on - like fuel and the design or make of the cremator and the ability of the furnace operative - we arrived at three major factors that determine cremation time. They are the peak temperature of the furnace and the sex, and we were very interested to see that males take significantly longer to incinerate than females, and that the younger the charge the longer the time, and the charge that was most difficult to incinerate in terms of time is a young male with a low furnace temperature. [...] Our statistician obliged us by drawing a graph in which he plotted the mean incineration time against the peak temperature of the furnace. Perhaps I had better explain this a little. At every peak furnace temperature there will be a scatter of times, there will be a scatter which he told us was a normal distribution, I must not go into this, around this point here at a temperature, a peak temperature, of 400 °C in the furnace, but the average, the mean out of all those recordings, came at 76 minutes which followed our original observation that the peak temperature of the furnace had a very important bearing on incineration time. From his graph he was able to tell us (we thought this rather interesting) that there is a maximum point, or rather a minimum point, of incineration time below which it is impossible to go, and our statistician defined this as a thermal barrier that, because of the make, the nature of human tissues, you cannot incinerate them at a rate which is below round about 63 minutes. Now some people will come up with readings of 60, 59, 58, they are the lower ends of this scatter of readings, and that this thermal barrier's optimum temperature is round about 800 - 900 °C.
Yesterday afternoon, when the representative of Dowson & Mason queried the temperature reading in Dr. Dunlop's paper and 850 °C was quoted, this is the point that we were talking about; this is the optimum temperature to incinerate charges; and as you pursue this, the time increases and then round about 1,000 °C it begins to decline. Our readings never went above 1,200 °C but our statistician said if we cared to extend our graph then he felt temperatures would fall; that is, if you built furnaces where you could have a temperature of 2,000 °C then obviously your time would fall, and the higher your peak temperature, once you had got beyond this thermal barrier, then your time would fall... [...] Our statistician colleague did some work, he looked into the records of crematoria in Germany during the last war, and it would appear that the authorities there were presented with a similar problem - that they came up against a thermal barrier. They could not design a furnace that reduced the mean incineration time to a very practical effective level. So we started to look at why there is this thermal barrier with human tissues.
We went and talked to a number of people about this - bio-chemists, medical people, - and it was suggested to us that human tissues are by and large made of protein and the proteins are exactly the same as you would find in other animals, but that at a high temperature they become de-natured. Instead of being joined together in a particular way they become dissociated and join together to form what can only be described as a hard shell. The bio-chemist we talked to said, 'Well, if you take an egg, nice and soft and you put it into hot water, three, four or five minutes later you get a hard-boiled egg, this is caused because the proteins of the egg have changed.' And it was suggested to us that when one heats a body to a high temperature, because of the nature of human tissues, of human proteins, they change, very similarly to a hard-boiled egg, and you get a casing of hard tissue like a lemon meringue pie. I apologise for the comparison, but the effect is that at 800 - 900 °C one had this thick shell, and no matter what one does in the furnace to have thermic lances, oxygen, gas fuel, one is always driven against this fundamental property of human tissue, that it will go hard in this temperature range..."

In the Q & A session, one of the questioners makes an interesting remark about attempts to speed up the process:

Mr. G.C.H. Sharpe: "[...] The other point was, he did mention the question of using oxygen. One crematorium with which I had dealings, although I was not there at the time when these experiments were carried out, did work with British Oxygen on oxygen lancing to try and speed up the cremation process, but all they found was that the oxygen lancing burnt holes in the body and did not speed up the process."

Then there is some data on gas consumption:

Dr. Jones (quoting from a document): "The average consumption of gas per body varies according to the number of cremations done in a day. When a high number of cremations is carried out the average consumption of gas is between 350 and 400 cubic feet of natural gas per body. With a low number of cremations the average is 400 to 450 cubic feet per body. When town gas was used (and in these two crematoria natural gas was used) the consumption varied between 950 and 1,100 cubic feet per body."

Natural gas is 1,030 Btu / cu ft. 1 Btu ~ 1055 J and 1,030 Btu = 1.09 MJ. So 400 cubic feet of natural gas is 400 * 1.09 MJ = 435 MJ = 14.5 kg of coke. In this case, the average body would have been a "normal" one, rather than moderately thin or emaciated. So it's between the 16 kg of the three-muffle and the 11.75 kg of the eight-muffle; and closer to the three-muffle's consumption. The bodies recorded in Dr. Jones' document would have been mostly elderly people, another reason why they would have been easier to cremate than the younger, thin, probably mostly male, victims at Auschwitz.

According to another source, "One [human] cremation uses as much energy in the form of gas and electricity as a 500 mile car trip, and releases a staggering 400 kilos of carbon dioxide into the atmosphere". When carbon is burnt, there is about 12 g of carbon for every 32 g of oxygen and 44 g of carbon dioxide, so 400 kg of carbon dioxide is generated from burning 109 kg of carbon, equivalent to 120 kg of coke. This is a far cry from the 1.6 kg of coke per body that Hoaxers require!

Another source reckons on "573 pounds of carbon dioxide", which is 260 kg of CO₂, and equivalent to 78 kg of coke. The report also tells of a new scheme that "dissolves human remains" using "one-seventh of the energy required for cremation". Unfortunately for Hoaxers, one-seventh of 78 kg of coke is still about seven times too much, and it's too late for them to start alleging the 'Nazis' had perfected such technology in the 1940s and the Topf ovens were merely a decoy to divert attention!

Modern animal cremators are much more economical than 78 kg of coke per human corpse; they can outperform 1940s technology, yet never achieve anywhere near the economy required by Hoaxers. A horse/cattle/pigs/fish incinerator consumes 6-7 liters of Diesel per hour at burn rates up to 50 kg/hr. Another incinerator for sheep and poultry and larger-sized pets is the same burn rate of up to 50 kg per hour, but Diesel consumption of 6 to 8 liters per hour. Taking the calorific value of Diesel fuel as 44.8 MJ/kg, the density as 0.832 kg/l, and a consumption of 7 liters per hour as associated with the maximum burn rate of 50 kg per hour, then 7 liters is 5.8 kg, which is 260 MJ, and equivalent to 8.7 kg of coke. So 8.7 kg of coke / 50 kg of animal tissue is 0.174 kg of coke for each 1 kg of animal tissue. The efficiency of this modern unit is better than the Kori animal carcasses incinerators that could only manage a best case 0.333 kg of coke per kg of animal tissue, which is not surprising since the Kori results were documented by W. Heepke in 1905. And there is no essential difference between cremating humans or animals; humans are quite similar to pigs. Nowadays, experts agree that "Incineration requires a great deal of energy compared with other disposal methods [such as rendering, burial and composting] and is not considered a viable economic disposal option due to cost and labor".

There is a large animal cremator for horses capable of a cremation rate of 300 lb = 136.08 kg per hour. So that's almost two-and-a-half times faster than the 55 kg / hr optimistic estimate for Topf coke ovens. But the burner maximum input rating is "5,275,279.25 KJ per hour". 5,275 MJ per hour is equivalent to 5,275 / 30 = 175.8 kg of coke per 136.08 kg of animal tissue. The same manufacturer offers a large animal incinerator capable of batch loads or continuous feed at an incineration rate of 550 lb = 249.48 kg per hour. The maximum input rating, including the cremation burner and afterburner, is "3,692,694.60 KJ per hour". That's 3,692 MJ / 30 MJ/kg of coke; which is equivalent to 123.1 kg of coke per 249.48 kg of animal tissue, or 27.1 kg of coke for a 55 kg human. (Then there's the electricity requirement of 220 volts at up to 64.5 amps, which is up to 51 MJ or 1.7 kg of coke per hour.)

Compare those figures with what Hoaxers need merely to make this particular aspect of their conspiracy theory work - 1.6 kg of coke to cremate a 55 kg body, which is 0.029 kg of coke per kg of human tissue. And that's before we count the durability of the firebricks, the duration of the cremation cycle and downtime of the ovens, the "cyanide gas chambers" with no cyanide residue on the walls, the delousing chambers with blue exterior walls, the "mind reading" and "incredible meeting of minds", etc.

With a requirement for 14 kg of coke for the moderately thin body in the eight-muffle - if we're very generous to the Hoaxers and pretend that all the ovens were as efficient as the eight-muffle (which of course they weren't), and with 1.6 kg of coke available per body after Hoaxers dropped their "four million dead" claim for Auschwitz, Hoaxers are faced with a deficit of 12.4 kg of coke per body. As demonstrated above, the idea that this deficit can somehow be made up by stuffing bodies together or by burning body fat is politically-motivated, pseudo-scientific claptrap.

Another ploy by Hoaxers is to argue that the records of coke deliveries to Auschwitz don't include the period after October 1943, and that therefore "any attempt to calculate how much fuel would have been needed per cremation based on known fuel supplies is futile". With that suggestion, Hoaxers really are scraping the bottom of the barrel!

In their fantasyland of 1.3 million murdered at Auschwitz, Hoaxers require 1,300,000 bodies multiplied by (an exceedingly low estimate of) 14 kg of coke per body, which is 18,200 tonnes of coke in total. The documented quantity delivered is 1,037 tonnes between February 16, 1942 and October 25, 1943, so they need to make up an additional 17,163 tonnes. In the earlier months the average monthly coke delivery was 30 tonnes, so after we allow them that for mid-January to mid-February 1942, they are still in need of 17,133 tonnes. From April through to October 1943 the monthly deliveries averaged 71 tonnes (497 tons over 7 months), and then Hoaxers need to propose that it suddenly rocketed to average 1,318 tonnes monthly (17,133 / 13) over the next 13 months (to November 1944)!

If the "extermination program" was decided in January 1942, why wait until November 1943 or later before carrying it out in earnest? And what a "coincidence" that it started just at the point where the coke delivery records are missing! And as David Irving pointed out, the fuel cellars at Auschwitz would only hold about twenty tonnes of coke. How would the "Nazis" keep thousands of tonnes of coke dry - possibly by having hundreds of thousands of Jews lying on top of it, with the added bonus that those who die from hypothermia don't need to be gassed? How do they make such a massive quantity of coke invisible in Allied aerial photographs - have the Jews wearing camouflage fatigues and face paint?

Even if Hoaxers claim that the February 1942 to October 1943 records are incomplete, they still need 18,200 tonnes over less than three years. Let's say three years, which is 505 tonnes per month. So they store twenty tonnes in the cellar, and the other 485 tonnes is kept outside and left to the elements??

If the "Nazis" really had been "exterminating" Jews on an industrial scale, apart from building massive industrial incinerators and gas chambers that worked, and not using their Zyklon B for delousing chambers, they'd have built massive cellars to accept the massive amounts of fuel required for the ovens. And the gas chambers would be on the same level, or higher than, the cremation ovens, rather than gas chambers in the cellar which necessitated having to drag thousands of cyanide-contaminated bodies up to the oven room.

The impossibility of using wood or motor oil to make up for the shortfall of coke

When Hoaxers attempt to make up the difference by suggesting some cremations were carried out in open pits, their claims are just as incredible. As mentioned above, open-air cremations require 160 kg of dry wood per body, or 300 kg of green wood per body. A Douglas fir, for example, provides 800 to 900 kg of merchantable wood. Let's say the open air cremators got one tonne of wood per tree. Each tree can cremate three or four bodies; say four bodies. Thus, the open air cremators need 25,000 trees for every 100,000 bodies that they cremate. And at Auschwitz, given the 1.3 million that were supposedly murdered and the 150,178 that could have been cremated given the coke that was available, they need to incinerate an extra 1,149,822 bodies, which needs 287,456 trees within three years, 95,819 per year, 262 per day, 22 per hour working from sunrise to sunset. Thus, the 22 trees per hour need to be felled, sawed and transported to the burning pits by the slave labor woodcutters. Then they have to conceal the fact that 287,456 trees are missing - perhaps by digging up all the stumps, burning them, burying the ashes, and inventing a novel, magical type of tree that grows to maturity within a month or two. They have to get rid of the mountains of wood and bone ash from the cremations. And they have to conceal this massive activity from Allied planes for three years.

(If we take the calorific value of dry wood as 19 MJ/kg, then with coke at 30 MJ/kg, the 160 kg of dry wood is equivalent to 101 kg of coke. The difference between that and the various figures from around 12 kg to 32 kg of coke per body in the Topf ovens is accounted for by the massive quantity of heat that is radiated and convected away in open-air cremations, compared to the much greater efficiency of the ovens.)

Hoaxers sometimes suggest "a little used motor oil" was burned in open pits to make up the difference; amusingly, the Hoaxers refuse to do calculations and instead resort to word-play sophism. They are well aware that any quantitative analysis spells doom for their 20^th-century religion. Let's be generous and assume a mere 40 kg per corpse, a ridiculously low assumption for open-air burnings. At around 0.87 kg/lit, it would take nearly 4.6 million liters of motor oil for every 100,000 bodies, or 52,891,812 liters for the required 1,149,822 bodies. Again, since there is no evidence of all that activity, the "Nazis" would have needed to find a way of concealing it, burning all the containers, disposing of all the physical evidence and the paperwork, and systematically eradicating the witnesses.

"Achtung! Berlin, ve need a little used oil. Ve haf some pigs to burn."
"Only 'ein bisschen', eh? That should be no problem. How much do you need?"
"About fifty million liters!"

Another solution for the Hoaxer is if he can get people to swallow the idea that the Germans were using about 30 kg of coke per body in their cremations (e.g., at the Gusen crematorium in November 1941), and then they suddenly conspired (in an incredible meeting of minds) to start a massive extermination program - not on German soil, but in an occupied territory - (whilst fighting the Soviets, the British, etc., and having already declared war on the US), and at the very instant they began the exterminations they suddenly hit upon a way of running the unsophisticated Auschwitz ovens so as to achieve fuel economy savings of around 95%, so that there was no sudden surge in coke consumption as the exterminations began - just as if no exterminations were carried out. And the miraculous fuel saving of 95% did not lead to any reduction in productivity. At the same time, they also came up with a way of extending the life of the refractory bricks by an order of magnitude. And bizarrely, they painstakingly recorded deaths due to natural causes whilst murdering at least ten times that number "off the books" - just as if no exterminations were carried out. Not to mention the fact that they used up 99.9% of their Zyklon B to save their prisoners' lives just as they were using the remaining 0.1% for killing them, whilst managing to leave no traces of cyanide on the walls of the "gas chambers" - just as if no exterminations were carried out. Or the fact that at the very same time as the Germans discovered this novel technology to cremate bodies with negligible fuel, they managed to combine it with operating the ovens for (12 hours x 1.3 million / 374,400 =) 41.7 hours per day! Moreover, the Hoaxer must propose that the Germans' super-ovens technology was mysteriously lost, and was never rediscovered by manufacturers of animal incinerators, for example - just as if such a technology never existed in the first place and no exterminations were carried out.

Although the answer - that there were no exterminations and such a technology never existed in the first place - should be obvious enough to anyone who can reject years of brainwashing and "think outside the box", no study of the "Holocaust" can be complete without looking into the feasibility of cremating with little or no fuel. Outside the realm of Hoaxer mythology, cremation ovens operate with hot gases flowing past the charge. The gas temperature should normally be approximately equal to the oven walls temperature, at ~850 °C or higher. During an endothermic stage in the cremation cycle (when heat is required), if the gas temperature temporarily falls below the walls temperature, an auxiliary power source will make up the difference. During the final stage as the bones calcinate and the combustible material has been consumed, the corpse continues to absorb energy, albeit at a slower rate as it approaches the temperature of the oven walls, which are able to sustain their temperature by way of the auxiliary power input. The rate of radiant heat transfer is proportional to the difference between the fourth powers of the absolute temperatures of walls and corpse - and gas and corpse provided the gas is a combustion product with significant emissivity (CO₂ or H₂O).

Cremation experts' views on fuel requirements for cremation ovens

There is an excellent Canadian publication Cremator Design and Performance - C.H. Beek (1979) in the public domain, including heat and mass balance calculations, and very detailed technical information on cremators. This 1979 version is best for those who like to work in BTUs and °F and generally is the better read; there is a 1989 revision showing the results in SI units, although this has the detailed calculations relegated to the Appendices. One of the main things to note is the substantial contribution from the coffin or casket. Under "Gross Heat Input from Charge" (p. 20 in the 1979 publication), there is 25,000 BTU (26.4 MJ) from the lacquer, 794,500 BTU (838.2 MJ) from the wood, 224,000 BTU (236.3 MJ) from the furnishing and clothes, and 378,000 BTU (398.8 MJ) from the body. Beek has based the calorific value for the body from what was believed to be a "reasonable average". Our calculations below, based on a reasonable estimate for the amount of fats, protein and carbohydrates in a typical Auschwitz victim, show that Beek's figure is indeed a fair estimate, but there are a few provisos. These figures are gross or higher heating values, they don't take into account losses in the heat of the smoke, they don't allow for the fact that lower heating values should be used for a furnace which is never going to recover the latent heat in the H₂O combustion product, and they assume no losses from insufficient combustion air. Moreover, there is the requirement to vaporize the water in the body and to heat the water steam to the exiting gas temperature. However, Beek has allowed for plenty of losses, such as "latent heat in H₂O from charge", and the difference between HHV and LHV in his "latent heat in H₂O from combustion".

Of all the energy sinks, the biggest by far is the requirement to heat the combustion air over the course of the cremation cycle. Continuing in Beek's 1979 article, by page 23 he's worked out a potential temperature of 2,096 °F (well in excess of his required 1,800 °F) in preliminary calculations, and then adds, "However, this temperature will not likely be reached in the ignition chamber without auxiliary fuel because of: (a) additional heat losses which we have not considered yet and (b) rapid evaporation of moisture during highest heat release rate" (that refers to heat released from the coffin). Since we want to know how much fuel it takes to cremate after the oven has been brought up to temperature, we can ignore the part about "Heat Storage in Walls". Under "Evaporation of Moisture" on p. 26, Beek makes the important point that from "numerous observations", there is no sharp rise in temperature at the stage of maximum heat release rate when the furnishings are being burned, because body fluid is being evaporated at the same time. Since the hypothetical exterminationist scenario has no coffin, furnishings, clothing and lacquer to burn, the first part of the cremation cycle is at least going to be endothermic rather than neutral, or at most very endothermic rather than moderately endothermic, and the temperature will certainly fall. The next phase is exothermic as the fats, proteins and carbohydrates burn, and the final phase is, crucially, endothermic. Beek remarks: "Maximum auxiliary heat requirement occurs during the calcining cycle when no combustibles are left in the charge".

On pp. 29-30, Beek's heat balance calculations indicate a gas temperature of 1,873 °F, and notes: "The overall heat and mass balance shows an excess of heat and would suggest that the burner inputs could be smaller. However, it does not differentiate between the various stages in the cycle and therefore does not indicate peak requirements."

That's an important point about peak requirements. The fats burn relatively quickly, and as we shall see, there is doubt as to whether the stack flow rate will be sufficient to pull in the stoichiometric amount of combustion air, especially when both corpses in an associated pair of muffles in the eight-muffle oven at Krema IV or V are simultaneously in the fat burning phase. The eight-muffle oven had 3-inch thick cast-iron doors for each muffle that could be used to shut off the combustion air, but the outside surface would reach a temperature of ~726 °C, at which point the conductive flow across the 124 °C drop between inner and outer surface would equal the heat radiated from the outer surface to the oven room. The Sonderkommando could hardly stand there holding the door part-open for minutes at a time. With the amount of heat emitted from the main air inlet door alone ranging from 1.5 (shut) to 2.3 kW (open), even by the time that's spread out to an area of 0.5 m² it's going to produce blisters and second-degree burns on exposed skin at 29 to 79 seconds. (There was one smaller door in the post-combustion - or ash - chamber, and one in the gasifier that fed a linked pair of muffles. As shown below, the door in the gasifier would be kept closed during cremations in the Hoaxers' alleged 1.6 kg of coke per body scenario; the gasifier would be used only for preheating.)

The other main thing to note from Beek's article is the amount of the "Net heat available to raise the temperature of the gases" that was required to achieve that 1,873 °F temperature: 3,391,552 BTU (3,578 MJ). There's 943,460 BTU allocated to "heat storage" which wouldn't be needed in continuous running (although by then conduction and convection losses would increase a little), so the 3,470,000 BTU from natural gas could be reduced by 943,460 (27.2%) accordingly. The 1.6 kg of coke per corpse that the Hoaxers have available can provide only a paltry 48 MJ (45,498 BTU) at best, even if we forget about losses in the heat of the smoke and the efficiency of the coke, not to mention the fact that it would have been counterproductive for the Germans to run the gasifiers in the 8-muffle oven at 3.2 kg of coke per hour per gasifier (1.6 kg per muffle), because the gasifier would be producing such a tiny output of CO in relation to the incoming combustion air that there are grave doubts over how much of that could burn to completion even in a turbulent, diffusion flame, and the 393.52 kJ/mol of carbon burned would turn back towards 110.53 kJ/mol, taking a retrograde step from the new semi-direct muffle heating that was brought in to economise on coke, back towards wholly indirect. And in any case, the gas temperatures would be so low that any CO₂ product, given its relatively high absorptivity, unlike nitrogen, would actually absorb radiant energy from the corpse and refractory walls. Full details of all that below for those interested in such things.

Beek's charge supplies a "Gross Heat Input" of 1,421,500 BTU, which is a far cry from the required 3,391,552 BTU. Back on page 20, it is seen that 73.4% of that is provided by the lacquer, wood, furnishings and clothes; the corpse manages only 378,000 BTU (~399 MJ, or 408 MJ after they've rounded their 140 lb corpse up to 65 kg in the 1989 revision). 1,043,500 BTU (1,101 MJ or 37 kg of coke at 30 MJ/kg) is attributed to the lacquer, wood, furnishings and clothes. The Hoaxer minimal fuel scenario together with naked corpses without a coffin requires that, unlike every other cremation oven in the world, the hypothetical extermination program involved a bizarre, novel "German method" of preheating the oven walls, and then attempting to operate continuously without any auxiliary heat source, hoping to be able to cremate by using the refractory material as a reservoir to provide radiant heat, whilst blowing cold air onto the corpses. It's rather like trying to drive around the world in a little electric car that's powered solely by a few flashlight batteries. Although things aren't too bad as the fats and proteins burn, the fatal flaw occurs during the final calcination stage.

Unfortunately for the Hoaxers, the corpse continues to give off heat to the cool gases via convection at an increasing rate as it warms up, at the same time absorbing radiant heat from the oven walls at an ever-decreasing rate as it approaches the wall temperature. Eventually, as we shall see, the corpse briefly reaches an equilibrium temperature about 16 °C below the wall temperature, at which its rate of convective heat loss to the air equals its rate of absorption of infra-red heat radiated from the walls. Moreover, since the walls are cooling as they lose heat by conduction and convection, the corpse temperature inevitably follows the declining wall temperature. After being briefly in equilibrium, the corpse proceeds to cool, following a temperature just above the equilibrium point, such that it's absorbing from the walls at a rate ~150W below its convective losses to the air, in accordance with its gradually declining temperature. This is easily demonstrated by the program provided, as described in the section on calcination.

The purpose of calcining the bones, the final stage in the cremation cycle

Calcination is an endothermic process. For example:

100.086 56.077 44.009
CaCO₃ ===> CaO + CO₂ (g) - 179.18 kJ
-1207.6 -634.9 -393.52

The first line shows the molecular weights in grams of reactant and products; the third line shows the heats of formation in kJ/mol, to demonstrate how the heat of reaction is derived. It is seen that the decomposition reaction absorbs 1.79 MJ/kg of CaCO₃, which is not much considering the CaCO₃ content is only hundreds of grams per corpse, but then there's several kg of calcium triphosphate, and it's endothermic nevertheless. If the Germans had been capable of oxidising the remaining organic material and calcining the bones whilst the charge was a net emitter of heat, they would have been the first to discover a way of violating the laws of conservation of energy, and could have used their new-found knowledge to wreak all kinds of mischief.

Although the final stage of calcination needs little combustion air in relation to the peak heat release rates as the fats - or coffin furnishings - burn, it still needs atmospheric oxygen. In his article, Beek suggests some ways of saving fuel, such as: "During the calcining stage when little air is required, the air supply for combustion of the charge could be reduced to 50%, resulting in a lower fuel consumption." Calcined bone is bone that "has been heated and oxidized sufficiently that all organics have been removed, and the apatite of the inorganic portion has been recrystallized to a more stable form than is found in unburned bioapatite. It is very light gray to white." When bone is exposed to heat in the absence of oxygen, it merely chars or carbonizes, and the black, pyrolysed product is bone char rather than calcined bone. In order to reduce the bones to a white bone ash, they must be heated in the presence of atmospheric oxygen, e.g., "calcined with free access of air in a small reverberatory furnace or a large muffle".

The purpose of calcining bones in cremations is not merely to ensure the destruction of pathogens and carcinogens - which murderous maniacs would not have been worried about - but to facilitate the final grinding of the bones into a white bone ash powder, which would have been of paramount importance to mass murderers desperate to conceal all evidence of their crime. It's accepted that "[c]alcined bone is pure white, friable, and porous, whereas bone that is not quite calcined (gray to white in color) is not as fragile and is quite strong." When Boyer's lectures on diseases of the bones was published in 1805, it was known that diseases such as syphilis could render the bones "as brittle as if they had been calcined".

A US-Israeli team conducted a study on the burning of animal bones. The bones used in the burning experiments were mostly from goats; the animals had died the previous autumn or winter in northern Galilee (Israel), and the researchers "deliberately burned bones to varying extents in controlled ﬁres, and subsequently examined their susceptibility to fragmentation (a.k.a. friability) and their mineral properties by infra-red spectroscopy". The results are displayed in color codes from 0 to 6; 0 denoting unburned, 3 is fully carbonized and completely black, and 6 is fully calcined and completely white. The pure white code 6 represents "the calcined (most advanced) phase of burning, at which point bones are most easily reduced to powder".

CalcinedBone photo CalcinedBone_zpsffba2df0.png

Source: Differential Burning, Recrystallization, and Fragmentation of Archaeological Bone - Mary C. Stiner et al (1995)

The infra-red spectra showed that the collagen peak at 1653 cm^-1 for the burn code 1 sample was greatly reduced in samples 2 to 6, with 6 having the least of all, and the carbonate peaks - easily visible in samples 1 to 5 - were almost totally absent in sample 6. The fully calcined sample 6 was shown to have recrystallized by its higher "splitting factor" - the average of the heights of the two peaks at 604 and 564 cm^-1 divided by the height of the trough between them. When the burned bone fragments were merely agitated vigorously inside a box for one minute, a sample size of 741 of the color code 3 bones averaged 6% powder by volume, compared to an 11% powder volume for 536 bones in code 5 and 6. Prior to agitation, the median size of bone fragments was 3.1 cm for code 4 bones and 1.4 cm for color code 6.

Isn't it preposterous to imagine that a nation of genocidal maniacs bent on "exterminating" millions of people on an industrial scale, and desperate to eliminate all evidence of the crime, would choose to resort to half-measures (or half-baked measures) by attempting to cremate with minimal fuel, making the grinding of more than six million pounds of bone remains (in just one "death camp" alone!) an even more colossal task, and leaving so much black char at the crime scene that they might as well have written signed confessions and nailed them to the walls of the oven rooms?

In any case, if the Germans had decided to settle for black bone char by shutting off the oxygen supply in the Topf ovens, they would be faced with the same fundamental thermal problem. Instead of getting only to within some 16 °C of the oven walls temperature, the corpse would approach it more closely, until the energy it absorbed was being used for endothermic decomposition and recrystallization rather than sensible heat. But then, as the oven walls cooled, the corpse would be obliged to cool too. Decomposition reactions would reverse, with CaO and CO₂ converting back into carbonate as the CO₂ partial pressure exceeded the equilibrium pressure over CaCO₃ at the lower temperature (and as the CO₂ built up in the unventilated chamber).

In short, any attempt to cremate with no auxilliary fuel source - or with a paltry 1.6 kg of coke per corpse - would have most certainly failed, and the Germans would have been left with 1.3 million partially cremated bodies, (1.3 million x 206 =) 267,800,000 bones to dispose of, and ~40 million teeth. They might have tried shutting off the combustion air inlet door, in which case they would have about six and a half million pounds of black, charred bones and bone char. That's great if they wanted to go into the water filter business, but useless for covering up evidence of genocide. We are told that almost 900,000 were murdered and buried at Treblinka, and then the "Nazis" became scared that "the evidence" might be discovered, and in a blind panic, spared no effort in digging up the 900,000, cremating every single one in open-air cremations, and disposing of "the evidence" without a trace. This is not consistent with an attempt to save 95% of the fuel at Auschwitz-Birkenau by resorting to semi-cremations, which in any case would ultimately have brought about an even greater panic and a requirement for thousands upon thousands of tons of coke in a belated attempt to dispose of "the evidence".

Those who want to skip the remainder of the calculations can jump ahead to the conclusion. In the discussion below, some details such as the calorific value of the corpse and the efficiency of the oven are included for completeness, but it wouldn't make any difference to the outcome whether the corpse yields 250 MJ or 500 MJ, or whether the oven is 65% or 75% efficient. If the exothermic fat-burning part of the cremation cycle makes up for the initial endothermic evaporation phase, the process will still fail in the final endothermic stage of calcination. (See here for a description of how the process fails, or for a bit more background, start here with how heat is inevitably absorbed at a rate of tens of thousands of watts - for a pair of linked muffles in an 8-muffle oven - by the "greenhouse gas" water vapor in the incoming atmospheric air.)

In Mattogno's reports on the Auschwitz-Birkenau crematoria ovens, he shows a heat balance equation devised for the Topf coke-fired double-muffle oven at Gusen, based on a model in a 1933 article by the engineer Wilhelm Heepke. The heat balance equation represents a situation where the oven is in thermal equilibrium; the refractory material has already been heated up to operating temperature, and the heat input to the oven equals heat losses out of the oven. The 30.6 kg of coke per corpse derives from available data for a period in October/November 1941, when 677 corpses were cremated and the total coke consumption was 20,700 kg.

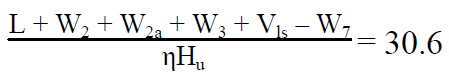
HeepkeHeatBalance photo HeepkeHeatBalance_zps9042ac0d.png

Source: Auschwitz: The Case for Sanity [p. 269] - Carlo Mattogno

(Also see Mattogno's The Crematoria Ovens of Auschwitz and Birkenau, [note 125].)

The 30.6 kg of coke on the right-hand side of the equation denotes the requirement from the auxiliary fuel source after adding up various energy sinks, deducting the contribution by the charge (W₇), and dividing by eta H_u which allows for the efficiency of the coke. And it's in good agreement with cremation experiments from 1927 performed by the engineer Richard Kessler, who found that cremations needed 29.5 kg of coke per corpse, excluding the amount needed to preheat the oven (which puts the requirement up to 54.5 kg per copse). Mattogno made some revisions to Heepke's model that brought the 30.6 kg figure down to 20.5 kg of coke per corpse for the Gusen double-muffle, and after allowing for the oven in the Kessler experiments still not being fully up to temperature, calculated a true equilibrium consumption of 23 kg of coke per body for Kessler's oven.

Again, as with Beek's calculations, the data from Gusen and Kessler includes the not inconsiderable contribution by the coffin and its furnishings and clothing. In agreement with Beek, the L denoting the requirement to heat the combustion air is going to be the largest energy sink by far. We'll concentrate on the eight-muffle Topf ovens at Crematoria IV and V, since these theoretically have the lowest coke consumption at 14 kg per body for a moderately thin corpse.

The absurdity and inefficiency of attempting cremations with minimal fuel

Given the design of the Topf ovens at Auschwitz-Birkenau, it soon becomes evident that it would have been absurd for the Germans to burn coke during cremations at around a tenth of the normal rate of consumption. The eight-muffle ovens, for example, had four gasifiers - one for each connected pair of muffles, and the recommended rate of coke consumption in each gasifier hearth was 35 kg per hour (17.5 kg per corpse, assuming one hour cremation times, which is the best that can reasonably be expected); see Mattogno, Auschwitz: The Case for Sanity [pp. 279-282 on cremation times; p. 261 and 264 on the hourly load of the hearth grid for the three- and eight-muffle ovens respectively]. The three-muffle ovens, with their two gasifiers for every three muffles, would equate to 23.3 kg per corpse at the rated load of 35 kg per hour. Once the ovens were heated up, some savings on the 17.5 kg/corpse and 23.3 kg/corpse figures might have been possible, but the Holocaust legend requires that the 'Nazis' improve on those rates by more than an order of magnitude.

There was a suggestion that under "continuous operation", the 35 kg per hour could be reduced by one-third to 23.3 kg/hr. Firstly, that applies to cremations with a coffin, which itself contributes the equivalent of 37 kg of coke, even according to analyses such as Beek from 1979. Secondly, the optimistic 11.7 kg/hr per corpse for the eight-muffle oven applies to "normal" bodies, whereas for those on the Auschwitz rations it is more appropriate to assume moderately thin or worse. Thirdly, after allowing for cleaning out slag and general maintenance of the ovens, true 24-hour operation would not be possible; the ovens would be operated for 20 hours per day. Thus, the 35 kg/hr of coke should be taken as the norm.

Old cremators used the very inefficient method of indirect heating, in which all of the combustion takes place outside the muffle, and the warm gases generated are allowed to flow into the muffle to heat the ovens walls, and then dry out and heat the corpse. This method did have the advantage that the ashes of the fuel remained entirely separate from the ashes of the corpse. After the impositions of the Versailles Treaty, Germany was forced to economize on coke consumption [ibid, p. 240], and legislation that only permitted completely indirect cremations was amended to allow a new semi-direct heating process.

For coke-fired ovens, the semi-direct heating works on the principle that the coke is burned in a gasifier that will "gasify" the coke, producing mostly carbon monoxide. This is done by burning the coke at a rich mixture with inadequate oxygen, so that combustion is incomplete. The gasifier's output of carbon monoxide, plus the inevitable nitrogen that comes along with burning fuel in air, and some carbon dioxide where the CO burns to completion, feeds the muffle containing the corpse. An excess of combustion air is supplied to the muffle - both for enabling the carbon monoxide to burn to completion to carbon dioxide, and to allow for burning of the corpse. This semi-direct method still has the advantage that the ashes from the coke are not mixed with the deceased's ashes, yet provides a major gain in efficiency. The C + ½O₂ ===> CO part of the reaction releases 110.53 kJ for each mole of carbon monoxide produced from a mole of carbon, whereas the CO + ½O₂ ===> CO₂ final part of the reaction releases 282.99 kJ for every mole of carbon dioxide produced from a mole of carbon monoxide. The 110.53 kJ is only ~28% of the 393.52 kJ per mole of carbon burned to produce a mole of carbon dioxide, whereas the 282.99 kJ released in the oven is ~72%. Thus, most of the energy released from burning the carbon is directed to the muffle. And it benefits from some of the heat remaining in the CO and nitrogen from the first step of the reaction, so the initial 110.53 kJ is only partly lost in the gasifier.

The process isn't as efficient as if the CO to CO₂ step occurred exclusively in the muffle, but for our model, let's favor the exterminationist thesis by supposing that the gasifier works perfectly.

However, the Auschwitz-Birkenau ovens' final muffle which lacked its own gasifier - the central muffle in the Topf triple-muffle oven and the last one of each pair in the 8-muffle - was still using completely indirect heating, as in the old technology. The first muffle gets the lion's share as heat is given out from the combustion products when their temperature decreases from the adiabatic flame temperature of somewhere (depending on the exit temperature of the gasifier) between 1,623 °C from the CO to CO₂ step and 2,183 °C from complete combustion to CO₂, right down to about 850 °C, and then the decrease in the final muffle is only from 850 °C to the final exhaust gas temperature, e.g., 650 °C. That massive inequality shows how the corpse in the final muffle would not have burned as well as the corpse subjected to semi-direct heating. Burning of the corpse in the final muffle is only at an advantage when the first corpse (or corpses in the three-muffle) is at an exothermic part of the cycle, and its hot gases can help to heat the second corpse. The gas residence time in the final muffle is lower, since the combustion products of the first corpse, plus any excess combustion air from the first muffle, all enter the second muffle in addition to the combustion air for the second muffle, and gasification generated from the second corpse. The final muffle in the eight-muffle also has greater conductive losses, through the outside sidewall.

(The gases never actually reach the adiabatic flame temperature because of dissociation reactions over 1,250 K - for example, some CO₂ would revert back to CO + ½O₂ at high temperatures - and because the heat is radiated away so rapidly at high temperatures to the walls or corpse. The former occurs because at very high temperatures, there is sufficient energy to decompose the products and prevent complete combustion. For example, some of the N₂ and O₂ forms NO, which has a positive heat of reaction of 90.29 kJ/mol, and some H₂ and O₂ forms OH, which again is an endothermic reaction, and so on. Hydrogen burning in air could hypothetically reach 2,247 °C if the equilibrium considerations were ignored; other sources that have calculated a theoretical T_AFT that takes into account the equilibrium constants may state 2,210 °C (2483 K). But all that doesn't stop the first muffle from receiving the benefits of that massive hypothetical temperature decrease. Here, unless otherwise stated, we'll quote the higher, hypothetical T_aft that ignores equilibrium considerations and assumes complete combustion regardless; it gives a better idea of how much energy is available for heating the corpse and oven walls - and is easily calculated.)

So this is how the ovens were designed to work - have one corpse per muffle cremated in about an hour if all goes well (although there's an inevitable cost from trying to save on fuel by having more muffles than gasifiers), have each gasifier hearth burning coke at a rate of 35 kg per hour during the initial heating of the ovens, with the potential for possibly reducing that slightly once cremations are underway. Now let's see what happens when the coke burning is drastically reduced to a tiny fraction of the original rate, specifically, 3.2 kg of coke per hour per gasifier hearth of an eight-muffle oven, which if it succeeds in cremating bodies in an hour, would cut the rate of coke consumption down to the Hoaxers' required rate of 1.6 kg of coke per body. (They'd need to achieve better than that during cremations, after allowing for the requirement to initially heat the ovens, and then reheat them again every time the ovens were down for maintenance. But let's stick to the 3.2 kg of coke per hour per gasifier for now.)

Determining the energy requirements in the cremation process

The problem is that a great deal of combustion air needs to be introduced into the muffles in order that the corpses can burn, in addition to that needed to allow the CO to burn to completion. It is well known that for a typical hydrocarbon, the oxygen required is ~1 g for every 13.1 kJ released, and this value will remain within a few percent for various H/C ratios. By considering the fats, proteins and fats content of a typical corpse, we can determine the rate at which oxygen - and air - is required to flow into the muffles to allow combustion of the corpses. We can also determine the volume flow rate from the chimney size and exhaust gas temperature.

In estimating the body composition of a typical Auschwitz hypothetical "gassed" victim, we shall take the average in the range of the three body types used in Mattogno's heat balance calculations: the moderately thin 55 kg body, which is between the 70 kg "normal" corpse and the 40 kg emaciated "Muselmann".

Revisionists like to talk about the energy needed to evaporate the water and break down the bones, whereas orthodox historians will prefer to concentrate on the energy released from burning the fat of the corpse. However the calculations are done, one thing that cannot be denied is that in theory, the energy potentially available from the fats, proteins and carbohydrates exceeds the energy required to evaporate the water and dispose of the bones, by quite a considerable margin. From the NIST database, calorific values for various proteins, carbohydrates, and fats (fatty acids and triglycerides) were averaged out to obtain generic values calculated as 16.51 MJ/kg for carbohydrate, 18.2 MJ/kg for protein, and 38.93 MJ/kg for fat. The generic formulae are CH_1.826O_0.913 for carbohydrates, CH_2.063O_0.626N_0.282S_0.008 for proteins, and CH_1.838O_0.118 for fats. [See the full text for further information.]

Those specific energy figures are gross, or higher heating / calorific, values. The lower calorific value is the higher calorific value less the energy required to vaporize the water (when the hydrogen in the fuel is burned, not to be confused with evaporating the water content of the corpse). For example, when 2.016 g of hydrogen is burned with 15.999 g of oxygen in the reaction H₂ + ½O₂ ===> H₂O to form 18.015 g (a mole) of water, the higher calorific value assumes the water product ends up as liquid rather than vapor, and is based on the -285.83 kJ/mol heat of formation (at 298 K) of water in the liquid state. So 285.83 / 2.016 is a yield of 141.78 kJ/g of hydrogen consumed. Fortunately, when animals burn up food, the combustion rate is sufficiently slow that the blood doesn't boil, the latent heat is not an issue, and the higher calorific value is obtained. But this is in complete contrast to the situation of fuel burning in a furnace. The adiabatic flame temperature of hydrogen burning in air is well over 2,000 °C, and in the furnace, after much of the heat released has been transferred to the surroundings, the water vapor product (mixed with nitrogen) remains nearer 1,000 °C than 100 °C. In this case, the energy released is based on the -241.83 kJ/mol heat of formation of water as a gas, and so 241.83 / 2.016 is a lower figure of 119.95 kJ/g of hydrogen consumed; which is around a 15% reduction. In carbon burning, the CO₂ product is still gaseous at room temperature so the distinction does not apply. Thus, the calorific values in the previous paragraph should be reduced by around 7½% for the case of combustion in a furnace or oven, depending on the hydrogen-carbon balance. That's in quite good agreement with Beek's [p. 25] deduction of 112,273 BTU for "latent heat in H₂O from combustion", which is 7.898% of his 1,421,500 BTU "Gross heat input".

Nevertheless, let's stick with the higher values for the moment.

The main energy sink at the start of the cremation cycle occurs since it is necessary to dry out the corpse by boiling its water content, and to bring the water steam up to the temperature of the exiting combustion gases. So we need to determine a negative calorific value for the water.

Given water's specific heat of 4,184 J/kg.K, then in order to raise it from 10 °C to 100 °C, each kg of water requires 4,184 * 90 J = 376.56 kJ. Then there is the requirement to vaporize the water, which is 2,257 kJ/kg, making an accumulated total of 2,634 kJ/kg. The optimum oven temperature (for the shortest cremation time, as stated by Dr. E.W. Jones in The Cremation Society of Great Britain conference in 1975) is 850 °C. The oven walls temperature - which is what the Germans would have to rely on for heating the corpse, since they've chosen to run the ovens with minimal fuel and cold incoming air - cannot fall below 600 °C, since at that point the corpse would merely carbonize and the cremation would certainly fail. After we've calculated the gas flow rate and residence time, it becomes apparent that given the high rate of heat radiated from the walls and the relatively low mass and specific heat of the gas, and its absorption coefficient at the infra-red wavelengths radiated by the walls, there is ample residence time and rate of heat transfer for the water vapor from the corpse to attain a temperature approaching the walls temperature.

In contrast, the nitrogen and oxygen of the combustion air have very low emissivity / absorptivity, and any radiant heat transfer from the walls to those gases is negligible.

Rather than having to incorporate a variable to account for various oven temperatures, let's suppose that the water vapor from evaporation of body fluids is heated to 600 °C before exiting into the flue ducts. The corpse may be much cooler than the walls, but as the gases exit into the outlet in the outer walls of the eight-muffle oven's lateral muffle (see Auschwitz: The Case for Sanity [p. 263]), they will be exchanging much more heat with the oven walls than with the corpse, and moreover, when the corpse is generating hot combustion products at the same time as body fluid is evaporating, the hot CO₂ and H₂O combustion products will be trying to heat the evaporated water beyond the walls temperature, just as the evaporated water will be absorbing a lot of energy from those spent gases that would otherwise have been transferred to the refractory walls. So the energy required to heat the water steam from 100 to 600 °C, given an average specific heat of 2.03 kJ/kg.K over the range, is 500 * 2.03 kJ/kg = 1,015 kJ/kg. Adding the original 2,634 kJ/kg to boil the water to 100 °C steam, the accumulated total is 3,649 kJ/kg. So we have -3.649 MJ/kg for water, 16.51 MJ/kg for carbohydrate, 18.2 MJ/kg for protein, and 38.93 MJ/kg for fat.

A typical 65 kg corpse has a chemical composition of: water 61.6% (40.04 kg); protein 17% (11.05 kg); fats 13.8% (8.97 kg); minerals 6.1% (3.96 kg); carbohydrate 1.5% (0.98 kg). The undernourished Auschwitz prisoner has lost another 10 kg, most of which would be water, fats and protein. Mattogno's moderately thin corpse is assumed to have lost 30% of body fat and 25% of protein. For a typical 55 kg victim, the composition would go rather like this: water 35.5 kg, which is a loss of 4.54 kg and puts the percentage at 64.5% (it would be high for well-fed people in peacetime, but consistent with concentration camp inmates), protein 8.3 kg (a 24.9% loss that brings the percentage down to 15.1% of the 55 kg), fats 6.4 kg (a 28.6% loss that brings the percentage down to 11.6%), minerals 3.9 kg (almost unchanged; now 7.1% of the total; the skeleton would obviously become a higher percentage of the total), and carbohydrates 0.9 kg (an 8.2% loss that leaves the percentage nearly unchanged at 1.6%).

When we take the calorific values above for fats, protein and carbohydrates, and allow a negative calorific value for water as calculated above, we have: protein 8.3 kg x 18.2 MJ/kg = 151.06 MJ; fats 6.4 kg x 38.93 MJ/kg = 249.15 MJ; carbohydrates 0.9 kg x 16.51 MJ/kg = 14.86 MJ; water 35.5 kg x -3.649 MJ/kg = -129.54 MJ, which totals +285.53 MJ, equivalent to 9.5 kg of coke. Excluding the cost of the water, the original example of a 65 kg human body has a calorific value of 566.5 MJ, and so its calorific value is 8.7 MJ/kg, less the cost of drying out the corpse. The corresponding figure for the moderately thin 55 kg specimen is 415.07 MJ, giving a calorific value of 7.5 MJ/kg less the drying out cost. (Note how the 415.07 MJ, less evaporation of water, less a relatively small amount for calcining the bones, is actually slightly higher than the 378,000 BTU or 398.8 MJ assumed by Beek in his 1979 publication, and he was calculating for an average body rather than moderately thin. So 415.07 MJ is a generous estimate for the fats, proteins and carbohydrates.)

In saying that the apparent 285.53 MJ surplus at this point is equivalent to 9.5 kg of coke, it must be pointed out that given the efficiency of the oven is around 65% (and this is a generous estimate), the amount of coke required is actually about 54% greater than the nominal amount. As a semi-direct heating of the muffle, there is a relatively small inefficiency involved in heating the gasifier, and then most of the loss is from the heat of the smoke. The coke is burnt in the gasifier hearth with a scarcity of oxygen, so that the carbon monoxide does not burn to completion until arriving in the first muffle of the linked pair, whereupon it meets fresh combustion air. The initial step of the reaction C + ½O₂ + 1.887 N₂ ===> CO + 1.887 N₂ + 110.53 kJ in the gasifier has an adiabatic flame temperature of 1,308 K (1,035 °C). If the carbon monoxide and nitrogen products typically emerge from the gasifier at 1,073 K (800 °C), the 110.53 kJ/mol of carbon burned, bound in the products at T_AFT, has been reduced to 82.445 kJ at 1073 K, and so 28.085 kJ (or 7.14% of the 393.52 kJ/mol from complete combustion) was lost in heating the gasifier walls. The remaining 282.99 kJ is released in the final CO + ½O₂ + 1.887 N₂ ===> CO₂ + 1.887 N₂ step to complete combustion. The following chart shows how much of that energy is lost in the heat of the smoke (which is CO₂ + 3.774 N₂ since there are two lots of 1.887 N₂) at various gas exit temperatures, taking the values from JANAF tables. The 28.085 kJ taken as lost in the gasifier is added to the heat of the smoke, the total is subtracted from 393.52 kJ, and the remainder available to heat the muffle and contents is divided by 393.52 kJ to obtain the efficiency.

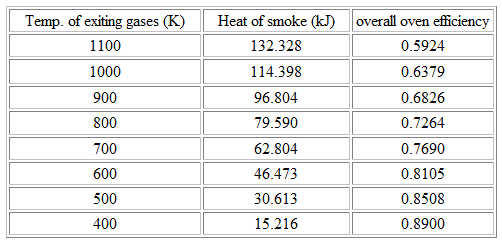
OvenEfficiency photo OvenEfficiency_zps9854aa80.png

Table 1

If the exiting gas temperature is 700 °C for example, the heat of the smoke at 973 K is 109.648 kJ/mol. (Values for intermediate temperatures are obtained by linear interpolation.) Add the 28.085 kJ lost in the gasifier, and deduct the total from 393.52 kJ, which leaves 255.787 kJ or 65% of the original 393.52 kJ available for heating the oven walls and / or the corpses, and places the practical heating value of the coke at 19.5 MJ/kg instead of 30 MJ/kg. Of course, 30 MJ/kg is an optimistic value for the heating value of the coke even at 100% oven efficiency, and doesn't allow for the fact that engineer Richard Kessler, the German cremations expert in the 1920s/1930s, found 21 kg (4.8%) out of a total sample of 436 kg of coke was "incombustible" slag; see Auschwitz: The Case for Sanity [pp. 282-283]. So an assumption of 19.5 MJ/kg of coke, when the exiting gas temperature is 700 °C, is being generous to Hoaxers.

Similarly, the 352 MJ to raise the temperature of the oven walls by 100 °C - which derives from 4,000 kg of refractive bricks in a pair of muffles multiplied by ΔT of 100 °C multiplied by the heat capacity of 880 J/kg.K - is nominally equivalent to 11.73 kg of coke. But after dividing by 0.65 to allow for the oven efficiency, it actually takes ~18 kg of coke. This particular measure of efficiency is going to be better when the oven is heated from cold, because the exiting gas temperature will be lower, but then the requirement to store heat in the walls is itself another type of inefficiency.

Anything with more than 50% moisture falls outside the shaded area in the Tanner triangle for assessing the combustibility of municipal waste, and is therefore not classed as "theoretically feasible for combustion without auxiliary fuel" [see p. 12, figure 2 at this link]. Another criterion for rejection is anything with an "average annual lower calorific value" of less than 7 MJ/kg, or any waste that fails to have a lower heating value of at least 6 MJ/kg "throughout all seasons" [see p. 9, ibid.]. In the example of the 55 kg moderately thin typical Auschwitz victim, even the higher calorific value is reduced to 285.53 MJ / 55 kg = 5.19 MJ/kg if the cost of vaporizing the water is included. The lower heating value would probably be less than 7 MJ/kg even before taking account of the water content. Beek assumed 2,700 BTU/lb (6.28 MJ/kg) as the heating value of the body.

Irrespective of whether the higher or lower calorific values are taken, they can never be realised in a furnace. They do not allow for any losses from the heat of the smoke, or from incomplete or non-combustion of the material. Any theoretical 5.19 MJ/kg higher heating value could be achieved only if the fats, protein and carbohydrates were at all times supplied with sufficient combustion air to burn to completion, and if the heat of the exhaust gases could be completely recovered by capturing all the CO₂ and water steam product, condensing the steam, and cooling the products down to the original pre-combustion temperature of around 20 °C. (Additionally capturing and condensing the water that was part of the reactants, not the products, would bring the yield up to 7.5 MJ/kg.) Of course, the Topf ovens at Auschwitz-Birkenau had no such facility; they were not even equipped with a recuperator or regenerator that could capture some of the heat of the smoke, let alone all of it.

Using the gross or HHV would predict too high a flame temperature and would need to be corrected for by incorporating the heat of vaporization within the proportion of the total energy released that is wasted by flowing out into the stack. From the LHV, the proportion of the energy that's lost in the heat of the smoke can be easily calculated from thermochemical tables showing various enthalpies for temperatures between ambient and the adiabatic flame flame temperature, such that the proportion lost in the heat of the smoke is given by the remaining enthalpy for the temperature at which the combustion products flow out of the oven into the flue ducts.

After evaluating the generic values (above) for the 15.6 kg of fats, proteins and carbohydrates in the typical 55 kg moderately thin Auschwitz corpse, there is 8.781 kg of carbon, 1.421 kg of hydrogen, 4.165 kg of oxygen, 1.152 kg of nitrogen, and 0.0752 kg of sulfur. The carbon yields 32.763 MJ/kg in complete combustion, so that's 287.69 MJ and with no need to specify lower or higher heating values; it's all the same. At the HHV of 141.78 kJ/g of hydrogen consumed, the hydrogen yields 201.47 MJ. At the LHV of 119.95 kJ/g of hydrogen consumed, the hydrogen yield is 170.45 MJ. Thus, the HHV total for carbon and hydrogen is 489.16 MJ; the LLV total for carbon and hydrogen is 458.14 MJ. Compare that with the 415.07 MJ from the higher heating value of the fats, proteins and carbohydrates. The 74.09 MJ difference in HHVs stems from the cost of decomposing the compounds. The sulfur content is negligible, and fortunately, oxides of nitrogen have positive heats of formation. If oxidation of nitrogen was exothermic, the world would be a very dangerous place; a single lightning strike would be catastrophic!

For a fair value of the potential yield of the corpse burning in a furnace or oven, we should deduct the 31.02 MJ difference between HHV and LHV for hydrogen from the 415.07 MJ total HHV for fats, proteins and carbohydrates, to obtain 384.05 MJ as the lower heating value of the combustibles in the corpse, before allowing for the cost of evaporating the water and breaking down the bones. That's about a 7½% reduction as expected, given that there are about twice as many hydrogen as carbon atoms, and so the number of moles of H₂O created is approximately equal to the number of moles of CO₂ created.

(This paragraph is just to show how it's more convenient to use the LHV in the case of an oven or furnace, for calculations such as losses in the heat of the smoke.) From the LHV, using the JANAF thermochemical tables, we can say that if the entire energy released from H₂ + ½O₂ + 1.887 N₂ ===> H₂O + 1.887 N₂ + 241.83 kJ remained in the products, they would be at the adiabatic flame temperature T_AFT of 2,520 K. If the gases had cooled to 727 °C (1,000 K) at the point of entering the flue ducts, then 26 kJ + 1.887 x 21.463 kJ = 66.5 kJ or 27.5% remains as the heat of the smoke, and 175.33 kJ or 72.5% has been transmitted to the oven walls or the corpses. That's 175.33 kJ / 2.016 g-H₂ = 86.97 kJ/g-H₂ available to do useful work. Going by the HHV, 285.83 kJ per mol of the products would correspond to the AFT of 2,520 K, and if the exhaust gases are at 1,000 K, the energy remaining in the products is 43.990 kJ + 26 kJ + 1.887 x 21.463 kJ = 110.49 kJ = 38.66% as the heat of the smoke. The oven and corpses get 175.34 MJ or 61.34%. (The 43.990 kJ/mol is water's heat of evaporation at 25 °C, and it is seen that the oven and its charge receive the same energy calculating from the HHV or the LHV. When calculating from the HHV, a greater fraction is lost in the heat of the smoke. But for the furnace, it's better to start out with the LHV; it avoids having to account for the latent heat of evaporation every time you want to do a heat of the smoke calculation.) This excludes the carbon, for ease in demonstrating the yield from the hydrogen.

So after multiplying those HHVs above (protein = 18.2 MJ/kg; fats = 38.93 MJ/kg; carbohydrates = 16.51 MJ/kg) that were obtained from the NIST database by 384.05 / 415.07 to get lower heating values, we obtain 16.84 MJ/kg for proteins, 36.02 MJ/kg for fats, and 15.28 MJ/kg for carbohydrates. (Proteins have the highest hydrogen content, so they should be lowered a little more, which is balanced out by fats and carbohydrates being lowered a little less. The effect of that would be to have the same total calorific value for the corpse, but to have an even greater difference between the exothermic peak during the fat burning phase and the endothermic evaporation phase.) The 415.07 MJ total from fats, proteins and carbohydrates becomes 384.05 MJ excluding the cost of drying out the corpse and breaking down the bones.

That 384.05 MJ is comprised of protein 8.3 kg x 16.84 MJ/kg = 139.77 MJ; fats 6.4 kg x 36.02 MJ/kg = 230.53 MJ; carbohydrates 0.9 kg x 15.28 MJ/kg = 13.75 MJ.

At this point we can get a fair approximation of the combustion air required, from the 13.1 kJ/g-O₂ consumed in typical hydrocarbon burning (this derives from C + O₂ ===> CO₂ + 393.52 kJ which works out at 12.298 kJ/g-O₂ and H₂ + ½O₂ ===> H₂O + 241.83 kJ which is 15.115 kJ/g-O₂; Clayton Huggett recommended use of the constant 13.1 kJ/g-O₂ consumed, for calculating heat release rates in fires burning conventional organic fuels, and noted that the figure was normally within 5% of that. The 13.1 kJ/g figure was cited by FEMA, for example, A.2.3 in their Appendix A accompanying their 2002 FEMA 403 "World Trade Center Building Performance Study".) So for the stoichiometric mix, the corpse's 384.05 MJ from fats, proteins and carbohydrates will require 384.05 MJ / 13.1 MJ/kg = 29.32 kg of oxygen. Given that oxygen is 23.2% of the atmosphere by weight, the mass of air required is 29.32 / 0.232 = 126.4 kg.

Peak requirements for combustion air

This would be fine if the corpse was a well-behaved fuel rather like natural gas or coal, and releasing its energy at a constant rate throughout the entire hour of the cremation cycle (assuming it's only an hour!). It would only need 126.4 kg of air per hour, 35.1 g/s. Problem is, the heat release rate is massively non-linear throughout that time. And that doesn't just apply to corpses that are cremated with coffins and furnishings. For the naked corpse without a coffin, there is initially no heat released, but there is a requirement to evaporate the body fluids, with the water vapor acting as a further energy sink as it absorbs energy whilst flowing to the outlet. Then there is the fat burning stage, with a very high heat release rate, overlapping with proteins and carbohydrates with slower heat release rates. The final stage of calcining the bones and oxidizing remaining organic material is endothermic, as in the initial evaporation stage, but atmospheric oxygen is still required or the bones will char rather than calcinate.

The cremator designer must provide sufficient combustion air to cope with the peak heat release rates, as seen by Beek's calculation of 3,470 lbs/hr for the charge, plus his additional 3,062 lbs/hr of combustion air for the natural gas. The Germans would originally have had to allow combustion air for the coffins and for the 35 kg of coke per gasifier per two muffles per hour in the eight-muffle oven. Hoaxers must propose that at the very time their alleged "meeting of minds" instigated the mass exterminations and homicidal gas chambers policy - whilst simultaneously continuing with the life-saving delousing chambers that consumed 99.9% of the Zyklon B (!) - they also came up with a new strategy of running the Topf ovens with cold air and hoping that the corpses could be cremated from stored energy after preheating the refractory walls. (They wouldn't have cremated with 3.2 kg/hr of coke per gasifier because (i) it could only heat a few minutes' worth of combustion air, or the temperature rise would be insignificant (ii) there is no evidence of Topf oven adaptations involving new air inlet holes drilled into every gasifier, that would be required for the correct fuel-air equivalence ratio so that the gasifiers could still function as coke gasifiers (iii) the hearths would probably need frequent re-ignition.) And Hoaxers must postulate that it's just another bizarre coincidence that there is not a single piece of correspondence from Topf concerning this brave new method of using the ovens for mass murder whilst craftily using so little fuel that it seems like the ovens were only ever used for legal cremations of victims who died from natural causes. Even if "code words" were used, there would have been reams of correspondence and instructions, such as:

"For the cremation of those workers who received special treatment, preheat the ovens to 850 °C, extinguish the fires in the gasifier hearths, and quickly introduce the corpses before the refractory material has time to cool. Remember to shut off the combustion air for the first ten minutes during the evaporation stage of the cycle. As you know, we have built additional chimneys and installed a mechanism for switching the flue ducts so that the exhaust gases can be directed to the new thin, short chimneys designed to reduce the draft during the calcining phase. It is no longer necessary to clean out the gasifier hearths daily; wait until the next shutdown, whereupon the slag can be removed when the ovens are cold, before preheating. Our technicians will be visiting Auschwitz to instruct you at the start of this new vermin disposal procedure, although I regret I shall be away on urgent business."

Beek said that if the cremation oven was not capable of handling the peak burning rate, "visible smoke would be emitted from the chimney". On the one hand, Hoaxers have a problem with the paucity of Allied photographs showing smoke from crematoria chimneys; there is one from August 20, 1944, showing smoke from one chimney at Krema III, and the Simon Wiesenthal Center even resorted to forging fake 'smoke' onto a photograph. Generous amounts of combustion air could help to prevent the visibility of smoke. But the scarcity of coke in relation to the numbers allegedly murdered shows that the lack of an abundance of photos depicting smoking crematoria chimneys is not evidence that a large excess of combustion air was used; it's evidence that the ovens were not used on the massive scale that Hoaxers allege for their extermination allegations. On the other hand, the new strategy of cold air ovens could not afford to waste potential heat generated from burning the corpse's combustibles by failing to provide sufficient air such that the corpse would merely gasify rather than combust. There would have been no other way to maintain the heat stored in the oven walls, after - as Hoaxers must postulate - the Germans had decided to make 95% fuel savings by shutting off the coke fires during cremations.

FEMA pointed out that given sufficient air, the heat release rate per unit surface area of fuel is equal to the incident heat per unit surface of fuel (the heat flux) times the heat of combustion divided by the latent heat of vaporization.

FEMAHeatReleaseRate photo FEMAHeatReleaseRate_zps38003bd9.png

Source: FEMA, Appendix A, A.2.1, World Trade Center Building Performance Study

So the incident heat flux and the latent heat of evaporation determine the fuel's mass loss rate, or gasification rate, and if there is sufficient oxygen for combustion, the heat release rate is then determined by the heat of combustion. In this case, the fire is said to be fuel-controlled. However, if there is insufficient combustion air, because the fuel is being evaporated too rapidly compared to the oxygen flow rate, the fire will be ventilation-controlled, and in this case the heat release rate will be within some 5% of the oxygen mass flow rate in g/s multiplied by 13.1 kJ/g-O₂. The thing to note about fuel-rich, ventilation-controlled burning is that the energy released per unit of fuel is well below the stoichiometric heating value of the fuel. For example, some fuel is merely volatized and will flow away out through the chimney (or window) without combustion because it lacks the necessary oxygen. Sometimes carbon will not burn to completion, so the yield per mole of carbon from forming carbon monoxide is 110.53 kJ rather than the 393.52 kJ from forming carbon dioxide.

In order to know the required mass flow rate of combustion air that will allow complete combustion of the fats and make available the 36.02 MJ/kg for fats as calculated above, which is potentially 36.02 MJ/kg x 6.4 kg/corpse = 230.5 MJ per corpse, we need to know the peak burning rate of the fats. The FEMA equation for heat release, or mass burning, rates, appears to predict a rate well above what would be expected. Nevertheless, we'll take it into consideration as a reference point for a high estimate.

The average heat of vaporization of a range of fatty acids at atmospheric pressure is 73.1 cal/g = 306 J/g.

From the Stefan-Boltzmann law, the incident heat flux per unit surface area of the corpse, transmitted from the muffle refractory walls, is:
q = ε x σ x (T_w⁴ - T_c⁴)

where: q is the rate of heat transfer between emitter and absorber in W, ε is the emissivity of the transmitting walls (dimensionless), σ is the Stefan Boltzmann constant 5.6704 x 10^-8 W.m-².K-⁴, and T_w and T_c are the absolute temperatures of walls and corpse respectively. (This refers to heat transfer by infra-red radiation; as we shall see later, the corpse is also cooled by the cold air flowing through the oven.) The emissivity of the corpse is also a factor, but the emissivity of a corpse is barely less than 1, and thus can be approximated as 1. For example, the emissivity of human skin is 0.99 or 0.98. So for the total heat transferred to the corpse by radiation, we have: q = A x ε x σ x (T_w⁴ - T_c⁴)
where: A is the corpse's surface area in m², as seen by the surrounding walls. (The walls radiate heat at a rate depending on their surface area. However, in the case of an absorbing, cooler object entirely surrounded by the hot object radiating the heat, the heat transfer rate is determined by the area of the absorber.)

1.3 m² is the value to take as the corpse's surface area. This is the figure used by Prof. Paul Schläpfer, one of the major experts on cremation in Europe in the 1930s; see Auschwitz: The Case for Sanity, p. 727, document 47.

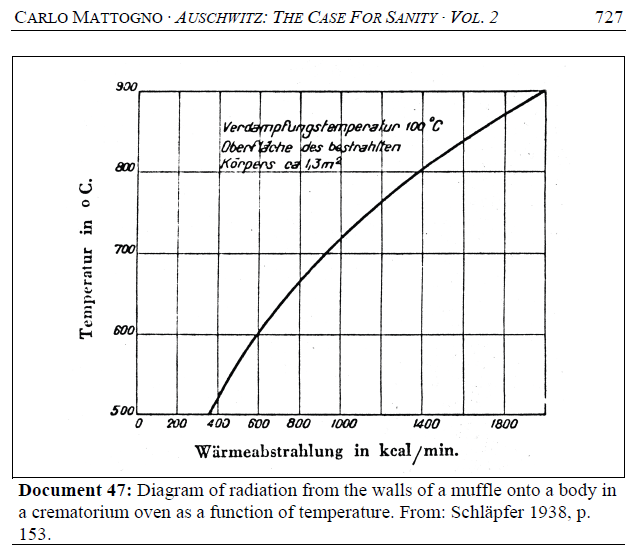
SchlapferQRadCorpse photo SchlapferQRadCorpse_zpsf6852514.png

Source: Mattogno, Auschwitz: The Case for Sanity, p. 727

Schläpfer's graph, which states a value of 1.3 m², shows the energy transferred by radiation from walls to corpse for wall temperatures from 500 to 900 °C. The corpse temperature is assumed to be 100 °C. After converting from Celsius to degrees Kelvin and from kcal/min to watts, it is confirmed that Schläpfer did indeed take 1.3 m² as the heat transferring area. And, interestingly, he assumed an emissivity of 1. For example, for his 100 °C corpse of effective surface area 1.3 m², at 600 °C walls temperature he has 600 kcal/min transferred between walls and corpse. That's 2.51 MJ/min = 41.8 kW. From:
q = A x ε x σ x (T_w⁴ - T_c⁴), if we set emissivity ε to 1 and put in the other values with the temperatures in K, we get 1.3 x 5.67x10^-8 x (873.15⁴ - 373.15⁴) = 41.4 kW. And for the walls at 800 °C, he has very nearly 1400 kcal/min, which is 97.6 kW. So 1.3 x 5.67x10^-8 x (1073.15⁴ - 373.15⁴) = 96.3 kW.

"Schamotte" brickwork has an emissivity of 0.85 at 20 °C and 0.75 at 1,000 °C (see section 8.4 at this link). And other values are brick, refractory, rough, 0.94; fire clay, 0.75 at 1,371 °C; and fire brick, 0.75 to 0.8 at 1,000 °C. The best guess would be an emissivity of 0.75 to 0.8 at the relevant temperatures. In order to be consistent with Schläpfer, and to give the Hoaxer allegations the best run for their (vast amounts of) money, we'll generally take the emissivity as 1, but will calculate the alternative in places to see how it compares. Since the Hoaxer legend precludes any possibility of cremating its alleged 1.3 million corpses of Auschwitz-Birkenau at a fuel consumption significantly greater than 1.6 kg of coke per corpse, the 'Nazis' would have had to rely upon a system in which the coke was used merely for preheating, an auxiliary fuel source with a capability to heat the air during cremations was regarded as a luxury for which the required fuel was not available, and the refractory brickwork was used as a heat accumulator that would somehow capture enough heat released during the fat burning stage in order to be able to release this during the endothermic evaporation and calcination stages of the cremation cycle (and would somehow withstand the thermal stresses to be able to cope with 25,000 cremations per muffle without the refractory brickwork needing to be replaced!!!). The lower the emissivity of the refractory walls, the lower their efficiency as a heat accumulator. For example, during calcination, the bones would be subject to a lower rate of heating from the refractory walls, whilst still receiving at least the same rate of cooling by convection from the cool air. Heat released by the corpse during fat burning would be transmitted to the air rather than the walls, but the air isn't going to store energy over the cremation cycle; it will simply transmit it up through the chimney and out into the wider environment.

The surface area of the skin of an average human adult is about 1.8 square meters as mentioned above, but because of the geometry, the walls do not "see" all of that area. Since some radiation is simply transmitted from wall to wall, in contrast with the "ideal" situation of a spherical body that is suspended in mid-air and surrounded by perfectly curved radiators, the 1.8 m² area is multiplied by a radiation view factor of less than 1; hence Schläpfer's use of 1.3 m².

On the other hand, the absorption coefficients of nitrogen and oxygen are low enough that we can ignore any radiative transfer from the walls to those gases. But some infra-red radiation will be absorbed by the water vapor in the air, and there will be convective heat transfer from the refractory walls to the air.

(In some of the more lurid "eyewitness" testimonies, if five corpses are stuffed into a single muffle, there is five times as much mass to burn, but the absorbing surface area is not going to increase five-fold to 6.5 m²!)

The fat-burning rate is clearly not going to be as high as the incident heat flux on the total surface area of the corpse divided by the fats' latent heat of vaporization, because the body isn't 100% fat. After most of the water has been evaporated, fat has become a higher proportion of the total. The original composition for the Auschwitz victim was taken as: water 35.5 kg, protein 8.3 kg, fats 6.4 kg, minerals 3.9 kg, carbohydrates 0.9 kg. Without the water, the fats are 32.8% of the remaining 19.5 kg total. However, given that the fats will be mostly located at about the same depth and will mostly burn at around the same time in the cremation cycle, the multiplying factor should be more than 0.328. Thus, the peak fat burning rate will be the rate at which heat is absorbed into the corpse, divided by the latent heat of vaporization of fat, and multiplied by a coefficient between 0.328 and 1.

From the Stefan-Boltzmann law, when the oven walls are at 850 °C, we have:
1.3 m² x 5.67 x 10^-8 x (1123⁴ - 473⁴) = 113.5 kW or 1.3 m² x 5.67 x 10^-8 x (1123⁴ - 553⁴) = 110.3 kW

It is seen that there is little difference in the heat transfer rate whether the fat is assumed to be at its boiling point of 200 °C or its auto-ignition point of 280 °C. After dividing 110,300 W by 306 J/g and multiplying by a coefficient of 0.5 to allow for dilution of fat, we obtain 180 g/s, and the 6.4 kg would burn in 6.4 / 0.18 = 35.5 seconds. Or setting the emissivity of the refractory walls to 0.75, the time will increase by 4/3 times to 47.3 seconds.

Both of those look much too high; the burning time would probably be a few minutes if the fat all burned at the same time, with the peak rate somewhat more rapid. In Mattogno's fat burning experiments, for example (see Auschwitz: The Case for Sanity, p. 393), in one case 200 g of fat (lard, pork fat) burned in 180 seconds which is 1.11 g/s, after several minutes of initial heating. Another took 225 minutes for 300 g of lard, which is 1.33 g/s. (Both featured "intense combustion" for all but 15 seconds of the total burning time.) The aluminium tray containing the fat in these two experiments measured 22 cm x 17 cm, a surface area of 0.0374 m². Thus, the average fat burning rate of 1.22 g/s works out at 32.62 grams per second per m². This compares with 50 g.s^-1.m^-2 in typical hydrocarbon pool fires, for which a somewhat higher burning rate might be expected.

Applying 32.62 g.s^-1.m^-2 to the corpse, then if the fat was at a constant depth, distributed over the entire 1.8 m² of the corpse, and all burned at the same time, the burning rate would be 32.62 g.s^-1.m^-2 x 1.8 m² = 58.72 g/s, in which case the 6.4 kg of fat would burn in 109 seconds. The time is then divided by the proportion of the surface that is burning fat at the peak burning time, and any burning proteins and carbohydrates must also be included. Alternatively, we could add to the 306 J/g heat of vaporization an extra 140 J/g for the heat of fusion, [2.348 J/g.K x (200-20) =] 422.6 J/g for sensible heat to raise the fat to boiling point, totalling ~869 J/g, and multiply by a factor of 0.25 to allow for some remaining water. So 110,300 W x 0.25 / 869 J/g obtains a mass loss rate of 31.7 g/s, which would burn the entire fat in 6.4 / 0.0317 = 202 seconds. Let's take this figure, forget the proteins and carbohydrates to be as fair as possible, and so the combustion air requirement for this peak burning rate of 31.7 g/s x 36.02 kJ/g = 1,142 kJ/s is 1,142 kJ/s / 13.1 kJ per g-O₂ = 87.17 g-O₂ required per second = (87.17 / 0.232 =) 376 g of air required per second = 1,353 kg = 2,982 lb of air required per hour, which compares with Beek's 3,470 lb of combustion air for the charge alone.

The massive energy deficit inherent in Hoaxers' mass exterminations conspiracy theory

Treating air as a nitrogen-oxygen mix, it requires 0.8959 MJ/kg to heat it from 20 °C to 850 °C (an average of 1,079 J/kg.K, which compares with 1,085 J/kg.K at 700 K), and so 1,353 kg of air requires 1,212 MJ over the hour, which is 20.2 MJ/minute. (That excludes the water vapor, which would raise the average specific heat a little, and becomes much more significant when we consider how the ovens would have to be operated.) It is easily seen that quibbling over whether there is a 100, 200 or 300 MJ surplus per corpse from the fats, proteins and carbohydrates, over the costs of disposing of the water and calcining the bones, pales into insignificance when the cost of heating the combustion air is included. The Germans would have been operating with a deficit of around 1 GJ per body, which is why their only hope would have been to attempt cremations with cold air and trying to cremate from heat stored in the refractory walls. (Although that wouldn't have worked either!)

If they continued to run the gasifier hearths as auxiliary fuel during cremations, they might have gained a little by keeping the inlet doors closed for the first ten minutes, but all corpses are different, and they cannot predict when combustion will start. If they open the inlet too late, they have lost more through merely gasifying instead of combusting some of the fats, than they would save by avoiding having to heat the air for another minute or two. The paltry absolute maximum of 48 MJ per hour per corpse from 1.6 kg of coke, if the oven was 100% efficient and we forget about losses in the heat of the smoke and from the incombustible slag, would provide for only 60 x 48 / 1,212 = 2.4 minutes' worth of combustion air over the 60 minute cycle. They need to supply air not only during the fats, proteins and carbohydrates burning phase, but also for calcining the bones, which takes about 30 minutes in a properly designed cremator such as recommended by Beek. With the exterminationists' required extraordinary new "Nazi" policy of attempting a 95% saving in fuel to cover up their crimes, cremations would have taken way longer than one hour per corpse, which is another reason why the cremations would fail.

It turns out that all of that 48 MJ/hr (less losses) provided by the 1.6 kg of coke, and even more besides, is swallowed up by various losses that are an unavoidable part of the cremation process. And that's if the distribution of CO was sufficiently patchy that it could burn in a non-premixed mixture when it would have no chance as a premixed flame due to being well below the lean limit for CO in air, and if the Sonderkommando were able to run the gasifier hearths at an order of magnitude below the recommended coke burning rate without the fire constantly extinguishing itself and having to be reignited. We'll look at that in more detail below.

As Beek says, fuel savings could be obtained by reducing the combustion air by 50% during the calcining stage. Even if the Germans managed to predict that every corpse started combusting at exactly ten minutes, say (it turns out to take rather longer than that!), so they open the air inlet then, and at thirty minutes they reduce the air by 50%, and they manage to cremate in 60 minutes whilst economising on fuel (a very optimistic assumption indeed!), the total consumption becomes 20.2 MJ x 20 minutes + 0.5 x 20.2 MJ x 30 minutes = 707 MJ. Suppose there is a surplus of 200 MJ from burning the fats, proteins and carbohydrates minus the water and calcining the bones. The auxiliary heat required is 507 MJ. Assuming 65% oven efficiency after losses in the heat of the smoke, and assuming a generous 30 MJ/kg from the coke, that leaves effectively 19.5 MJ/kg of coke, and so the amount of coke required per corpse is ~26 kg, which takes it up to the sort of level that can be in accordance with the law of conservation of energy, and is at least an order of magnitude from what is available in the exterminationist legend.

Specifications of the Topf eight-muffle oven at Birkenau

We'll concentrate on the eight-muffle oven (see Auschwitz: The Case for Sanity [pp. 262-265 and 271], which at 14 kg of coke for the "medium" (moderately emaciated) corpse in Mattogno's heat balance calculations has the best chance of achieving 1.6 kg of coke per corpse if by some magic the Germans had discovered a novel cremation technique, which was lost after the war and never subsequently rediscovered by manufacturers of large animal incinerators.

Crematoria IV and V each had an eight-muffle oven. There were two chimneys, and four gasifiers, per oven. With the rated load for each gasifier hearth at 35 kg of coke per hour, a one-hour cycle would amount to 17.5 kg of coke per cremation. Each gasifier fed a linked pair of muffles; the carbon monoxide produced by the gasifier would burn to completion on entering the first muffle at the gasifier neck in the muffle's sidewall, flow into the second muffle, flow out into a duct that merged with another duct from another muffle-pair, with the exhaust gases from four muffles flowing into a chimney that had a square cross-section of 0.8 m x 0.8 m and a height of 16.87 meters. There were no forced-draft devices, and so the exhaust gases were driven solely by the natural draft of buoyancy. The combustion gases flowed across the muffles from side to side.

The weight of the refractory brickwork in the eight-muffle oven was ~24,100 kg. The four gasifiers comprised about one-third of that, leaving a little over 16,000 kg for the eight muffles. If each gasifier had the same amount of refractory as the average muffle, then each would have 2,008 kg. And the refractory material for the muffles was 15 cm thick, as in the diagram below. The Topf double-muffle ovens had 7 cm of insulating brick and 20 cm of normal bricks on the exterior; Schläpfer shows 7.5 cm for the insulating bricks, which is almost identical.

Looking at an eight-muffle oven from left to right, there is the left exterior muffle, the left interior muffle, the left gasifier, the right gasifier, the right interior muffle, and the right exterior muffle. The coke burns to CO with a scarcity of oxygen in the gasifier hearth, the gas enters the interior (or first) muffle and burns to completion, and the hot gases are then fed into the exterior (or second) muffle. At the other side is another set of four muffles, with each set joined back to back. Thus, each muffle shares a back wall with the corresponding muffle from the opposite set of four, and each muffle also shares a sidewall with the adjacent muffle that links to it. The main chamber of a muffle is 700 mm wide by 800 mm high by 2,000 mm long, but the post-combustion (or ash-) chamber is about 340 mm high.

From the front, the arch corresponds to a semicircle of radius 350 mm, area 0.192 m², and with the length of the half-circumference at 1.1 m. After deducting 350 mm for the height of the arch, that leaves 450 mm for the height of the main chamber, and after adding 340 mm for the ash chamber, the height is 790 mm up to the start of the arch. We'll take the whole 1.1 m length of the arch as the top, so that the long sides have a height of 0.79 m, and the front and back will include the area of the semicircle. Here's the likely configuration:

Outer muffle, refractory material:- Exterior side, 2 x 0.79 x 0.15 m = 0.237 m³. Shared back wall, (0.79 x 0.7 + 0.192) x 0.075 m = 0.056 m³. Front, (0.79 x 0.7 + 0.192) x 0.15 m = 0.112 m³. Top, 2 x 1.1 x 0.15 m = 0.33 m³. Bottom, 2 x 0.7 x 0.15 m = 0.21 m³. Shared side partition, 2 x 0.79 x 0.075 m = 0.118 m³. Total, outer muffle, 1.063 m³ x 2,000 kg/m³ = 2,126 kg. Inner muffle, refractory material:- Shared side with gasifier, 2 x 0.79 x 0.075 m = 0.118 m³. Shared back wall, (0.79 x 0.7 + 0.192) x 0.075 m = 0.056 m³. Front, (0.79 x 0.7 + 0.192) x 0.15 m = 0.112 m³. Top, 2 x 1.1 x 0.15 m = 0.33 m³. Bottom, 2 x 0.7 x 0.15 m = 0.21 m³. Shared side partition, 2 x 0.79 x 0.075 m = 0.118 m³. Total, inner muffle, 0.944 m³ x 2,000 kg/m³ = 1,888 kg. Average refractory per muffle = 2,007 kg, which leaves about 2,011 kg for each gasifier.

The total surface area (m²) is 2 x 0.79 + (0.79 x 0.7 + 0.192) + (0.79 x 0.7 + 0.192) + 2 x 1.1 + 2 x 0.7 + 2 x 0.79 + 2 x 0.79 + (0.79 x 0.7 + 0.192) + (0.79 x 0.7 + 0.192) + 2 x 1.1 + 2 x 0.7 + 2 x 0.79, which amounts to 16.5 m² for the pair of muffles.

Although the refractory brickwork depicted in Schläpfer's diagram below from 1938 is not quite the same as the Birkenau ovens, the differences are small, and it gives an excellent illustration of the distribution of temperatures within the brickwork at various times from the start of preheating the ovens up to thermal equilibrium, when the energy going into the walls equals the amount that is lost by conduction and convection to the exterior. From this diagram it looks like around 20 hours would be needed to bring the walls up to equilibrium; which at 35 kg of coke per hour is 700 kg of coke (for two muffles). However, the amount of coke required is really much less than that; in Schläpfer's example of constantly heating the walls to 600 °C, he would not have needed as much as 17.5 kg per muffle per hour.

It's immediately evident that the inside surface of the brickwork gets right up to the required temperature very quickly. This is not good news when it comes to the efficiency of the preheating process. Even though there is initially less energy wasted in conductive losses, and more energy is being stored in the brickwork which can later be used to help perform work, of more importance is that right from the start, losses in the heat of the smoke will be relatively high. If the surface is being heated to 850 °C, the temperature of the exiting gases will be around that during the preheating, rather than being at an average of 435 °C as it heats up from 20 to 850 °C, and so from the table above the oven efficiency is going to be up in the top (or worst) area of that table around 1100 K where there is ~130 kJ/mol of carbon burned lost in the heat of the smoke, making the oven efficiency around 59% including some losses in the gasifier. In the case of 700 kg of coke over 20 hours, and assuming an optimistic heating value of 30 MJ/kg from the coke, the walls receive around 0.59 x 30 = 17.7 MJ/kg of coke = 12,390 MJ. But that's much more than enough.

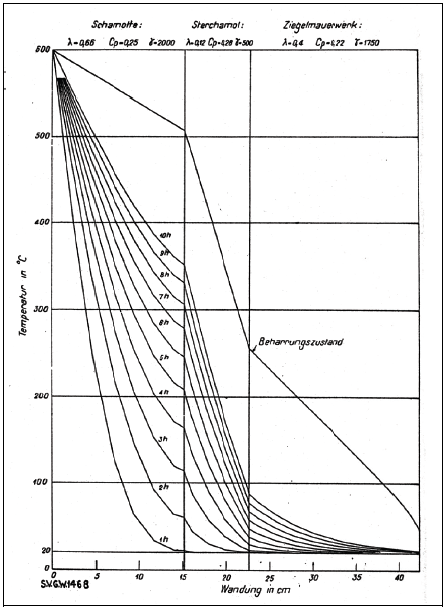
$RefractoryThermalGradient photo RefractoryThermalGradient_zpsd60a252a.png$

This is to show more clearly the values for thermal conductivity, specific heat and density (shown below in that order from left to right).

$RefractoryThermal photo RefractoryThermal_zpsbf76bf15.png$

Source: Auschwitz: The Case for Sanity [p. 727, Document 48] - Carlo Mattogno

In Schläpfer's example of heating to 600 °C, when we average out the temperatures, the refractory material ranges from 600 to 505 °C, an average of 552 °C which makes ΔT = 532 °C. The insulating bricks are at an average temperature between 505 °C and 255 °C, an average of 380 °C, making ΔT = 360 °C. The normal bricks average 160 °C, making ΔT = 140 °C. The refractory material has Cp = 0.25 kcal/kg.K = 1046 J/kg.K, density of 2000 kg/m³, and depth of 0.15 m, so each m² weighs 0.15 x 2000 = 300 kg, and the energy required to heat it is 300 x 1046 x 532 = 166.9 MJ. The insulating bricks have Cp = 0.28 kcal/kg.K = 1172 J/kg.K, a density of 500 kg/m³, and depth of 7.5 cm, so each m² of material has a mass of 0.075 x 500 = 37.5 kg, and the energy required to heat it is 37.5 x 1172 x 360 = 15.8 MJ. The normal bricks have Cp = 0.22 kcal/kg.K = 920 J/kg.K, a density of 1750 kg/m³, and depth of 20 cm, so each m² of bricks weighs 0.2 x 1750 = 350 kg, and the energy required to heat it is 350 x 920 x 140 = 45.1 MJ. The total per m² is 227.8 MJ, or 393 kJ/m² for each °C that the inside surface is raised above 20 °C. So the energy required for 850 °C at the inner surface, with the outer surface of the normal bricks barely above ambient temperature, is ~326 MJ per m² of wall.

This can be compared with the energy required to raise the whole material to 850 °C. The total is (300 x 1046 + 37.5 x 1172 + 350 x 920) x 830 = ~564 MJ, so the area under the curve is about 57.8% of the diagram. Another comparison is with the 166.9 MJ to heat the refractory brickwork when it takes 15.8 MJ for the insulating bricks and 45.1 MJ for the normal bricks, and so the total is 227.8 / 166.9 = 1.365 as a multiplying factor to calculate the total requirement for all three types of brick, given the requirement to heat the refractory bricks. Since the inner partitions don't need insulating and normal bricks, the 1.365 could be reduced somewhat.

After the oven has been preheated to thermal equilibrium at 600 °C (ΔT = 580 °C) in Schläpfer's diagram, the other side of the refractory material adjacent to the insulating bricks is 505 °C, 95 °C below the inside surface temperature. This suggests that when the surface facing the corpse is in equilibrium at 850 °C (ΔT = 830 °C), that other side would be at (850 - 95 x (830 / 580) =) 714 °C. Under equilibrium then, for the Birkenau oven, with temperature T_surface = 850 °C at a depth d of 0 cm, and T = 714 °C at d = 15 cm, and a linear function so that the midpoint at d = 7.5 cm has a temperature 782 °C which is the arithmetic mean of 850 and 714 °C, the temperature T_depth for 0 < d < 15 cm is given by T_depth = -9.0667 d + 850. The average temperature is 782 °C making ΔT = 762 °C.

Mattogno gives a value of 0.21 kcal/kg.K for the specific heat of the refractory material in the Birkenau ovens, which is ~880 J/kg.K. Schläpfer has 0.25 kcal/kg.K for his Schamotte, but we'll take Mattogno's figure for the moment. As for thermal conductivity, we'll have to use Schläpfer's data. He has a figure of 0.66, but his other diagram of energy radiated from the walls to the corpse has units of kcal/min, and 0.66 W/m.K looks a little low for refractory bricks. We'll assume that he used kcal/hour.m.K, and so the conversion works out at 0.767 W/m.K.

Assuming 4,000 kg of brickwork for two muffles in the eight-muffle oven, and specific heat of 0.21 kcal/kg.K, say 880 J/kg.K, the energy requirement (neglecting conductive losses through the three layers of brick) is 4000 x 880 x 762 = 2,682 MJ, or 3,352 MJ after allowing 25% for the insulating and normal bricks.

Taking the oven efficiency during preheating as 59%, which equates to 17.7 MJ/kg of coke available for heating the pair of muffles, the amount of coke needed is 3,352 / 17.7 = 189.4 kg. At 35 kg of coke per hour in the gasifier, the time required is 5.4 hours. It would take longer than that, since the first muffle adjacent to the gasifier would heat up more quickly. It's getting the lion's share of the heat of reaction when the carbon monoxide burns in the first muffle to completion, and the second muffle is only indirectly heated after the combustion products have already given off their heat to the first muffle. If we suppose that cremations can begin after preheating with 189.4 kg of coke, then given that Hoaxers have available 1.6 kg of coke per body, this amount of coke was supposed to have cremated 118 corpses. That's just for one gasifier and its two associated muffles, so preheating of all eight muffles would require an amount of coke that was supposed to have cremated nearly 500 corpses.

The evaporation phase - determining how long it would take

If the curve of temperature versus depth into the refractory brickwork was flat, at 850 °C from the surface facing the corpse along to the surface adjacent to the insulating bricks, and we ignore the insulating bricks and normal bricks, then each °C change in temperature would be worth 4,000 kg x 880 J/kg.K = 3.52 MJ. Of course, it doesn't work like that. After preheating the temperature decreases with increasing depth, but after the charges are loaded into the muffles, the corpse-facing surface is going to cool relatively quickly as it loses heat via radiation to the corpse, and via convection to the cold air if the inlet is open. The other side of the refractory material, against the insulating bricks, will cool at a slower rate, and the temperature gradient will slope the other way.

Given the fact that Hoaxers need to hope that their alleged 1.3 million bodies could all be cremated using the heat stored in the refractory walls, because the claimed death toll would leave the Germans with insufficient coke to heat the air in the ovens, that raises the interesting question of how much the exposed surface of the refractory material will cool when the auxiliary heat source is removed and the stored heat is used to dry out the corpses. The evaporation phase of the cremation will obviously take longer without coke burning, and the techniques below indicate how much longer. We shall also consider the case of multiple corpses per muffle.

Since the specific heat of the refractory material increases a little with temperature, and we want to be as fair as possible to the exterminationist thesis, we'll raise the refractory specific heat from 0.21 kcal/kg.K or 880 J/kg.K to 930 J/kg.K for subsequent analyses for determining how quickly the refractory walls cool.

In the case of a plane wall heated uniformly to some temperature T_i, and then at time t = 0 the heat source is removed and the wall starts cooling from convective losses to cold air at temperature T_∞, the temperature distribution at various points between the surface and the midplane can be calculated for subsequent times. The diagram below shows an example in which a plane wall exposed to convection has the surface temperature dropping most of the way down to T_∞ when the temperature drop has penetrated less than halfway towards the midplane. That would have the surface temperature dropping rapidly before relatively little of the energy had been transferred, increasing the transfer time. But it's not as bad as that for the extermination legend. When we go on to estimate the Biot number, it's not as high as implied in the diagram below, although it is clearly much too high to use the "lumped capacitance" method of calculating temperature decay (only applicable for Bi < 0.1), where the resistance to thermal conduction within the solid is very low in relation to resistance to heat transfer out of the solid, and the temperature gradients within the solid can be assumed to be negligible.

Mathematically, the case of a wall insulated at one side (as with the insulating bricks and the normal bricks on the other side) is the same problem as for a wall exposed on both sides, except all of the temperature decline occurs across the distance 2L instead of two symmetrical declines over L, and the midplane temperature is instead the temperature on the insulated (adiabatic) side. (There is also some heat loss through the insulating bricks, which we'll neglect for simplicity.)

PlaneWallTransientConduction photo PlaneWallTransientConduction_zpscd95253f.png

Source

The following shows the effect of the Biot number, which is going to be greater than 1, but not the ">>1" of ten or more times greater.

PlaneWallTransientConduction2 photo PlaneWallTransientConduction2_zps1358678b.png

Source: Incropera & DeWitt

It turns out that in the exterminationist 1.6 kg/coke per body brave new "German method" of using fuel merely for preheating, with the corpse being heated by stored energy in the oven walls, there certainly would be a requirement to heat the steam until it approached the temperature of the refractory walls. As shown below, infra-red radiation from the walls would be absorbed at a considerable rate by water vapor in the muffle, and so it is reasonable to assume a figure of 600 °C. At an average temperature of 350 °C or 623 K, the specific heat of water vapor is 2.03 kJ/kg, and so it requires 2030 x 500 = 1,015 kJ/kg to raise from 100 to 600 °C. It takes about 2,634 kJ/kg to heat water to 100 °C and boil, and so as calculated above, the total requirement becomes 3,649 kJ/kg, and 35.5 kg x 3,649 kJ/kg = 129.5 MJ to dispose of the water in the corpse.

Let's suppose 75% of the water evaporates before the fats start to release energy; so treating the linked pair of muffles as a system, that's 194.25 MJ lost from the oven walls, before counting other losses, and assuming the Sonderkommando manage to close the air inlet for the evaporation phase (in contravention of Topf's instructions).

In the general problem of the plane wall, the variables are reduced to dimensionless numbers. The Biot number Bi is determined from various physical characteristics of the system, and the Fourier number Fo is a dimensionless time that relates the actual time to physical properties of the solid. Given these two, the temperature can be calculated for various times and depths into the solid. From knowledge of the temperatures at, say, 101 equally spaced points at different depths, it is easy to find the average temperature and the quantity of heat that has been transferred out of the solid. Generally, it is supposed that the thickness is sufficiently small in relation to the length and width of the wall that a solution for one-dimensional conduction can be used. The thickness of the refractory layer per muffle is either 75 mm or 150 mm, whereas the other dimensions are 700, 790, between 790 and 1,140, 1,100 and 2,000 mm. If the corners were missing, heat would be conducted along from the center of each wall to flow out at the corners. The corner of the long sides on the top has been allowed for with the arch. There is a small amount of mass in the other corners that hasn't been counted, so the total mass of refractory could have been marginally increased, or the average thickness could have been marginally reduced. It would not significantly change the results, and since there wouldn't have been gaps at the corners, heat conduction to the corners would not be significant, and the problem can be treated as one-dimensional transient conduction.

The Fourier number is Fo = αt / L², where t is the elapsed time in seconds since cooling began at t = 0, L is the thickness in meters (the distance to the midplane if heat is lost from both sides, or the full thickness if one side is insulated), and α is the thermal diffusivity in m²/s. α is equal to k / (C_p x ρ), where k, the thermal conductivity of the eight-muffle refractory brickwork, is 0.767 W/m.K, C_p, the specific heat of the refractory, is 930 J/kg.K, and ρ, the density of the refractory material, is 2,000 kg/m³. Thus, the thermal diffusivity of the refractory material is 4.124x10^-7 m²/s. L in the case of the refractory brickwork is a little under 15 cm, allowing that each muffle probably has half the thickness on the shared partition walls. Taking the figures calculated above, there is 2,007 kg of refractory per muffle (averaging between the inner and outer muffles), the surface area totals 8.25 m² for one muffle, and so the average thickness is 2,007 kg / (8.25 m² x 2,000 kg/m³) = 12.2 cm. From these known variables, the Fourier number (or dimensionless time τ) can be calculated from Fo = αt / L² or Fo = 2.771x10^-5 x t. It is interesting to know the time corresponding to Fo = 1, which, from t = L² / α, is 36,091 seconds = 10.025 hours.

Let S = s / L be the dimensionless distance of a point from the midplane for the shared partition walls, or from the insulated surface in the case of the remaining walls, where s is the distance from the midplane or insulated surface (m), and L is the distance from the exposed surface to the midplane or insulated end as appropriate. Let θ(S, τ) = θ_s / θ_i, where θ_i is the initial temperature difference (T_i - T_∞), θ_s is some subsequent temperature difference (T_s - T_∞), T_i is the initial temperature of the solid, T_s is some subsequent temperature at a given time and distance from the center or insulated end, and T_∞ is the temperature of the free-flowing fluid that the surface of the solid is exposed to. Thus, the dimensionless temperature θ(S, τ) can be found from the dimensionless space and time variables S and τ, and from other physical properties of the system that are assumed to remain constant.

After finding the Biot number Bi, there is an exact solution for the case of the plane wall with an initial uniform temperature being subject to sudden convective conditions. However, we are interested in the situation of the refractory walls being subject to preheating, and then as the auxiliary heat source is removed (as required by the exterminationist scenario) and the charges loaded, the walls are subject to radiative transfer to the corpses. If the air inlets were left open, convection would be significant too, but to give the exterminationist thesis the best run for its money, we suppose that the air inlets are closed as soon as the cremations commence. We'll first describe the solution for the case of convective losses from the solid, and then adapt that to give an approximation for the radiative transfer from walls to corpses.

The Biot number is the resistance to conduction within the solid divided by the resistance to convection across the fluid boundary layer. If one surface of the solid is maintained at a temperature T_i and the other surface is exposed to a fluid of temperature T_∞, the system will reach a steady-state equilibrium with the exposed surface at some intermediate temperature T_s that equalizes the rate of conduction and the rate of convection. The rate of conduction within the solid is:
q_cond = (T_i - T_s) x k x A / L.
The rate of convection across the fluid boundary layer is:
q_conv = (T_s - T_∞) x h x A.

At thermal equilibrium, q_cond = q_conv and so (T_i - T_s) x k x A / L = (T_s - T_∞) x h x A. This rearranges to:
(T_i - T_s) / (T_s - T_∞) = (L / (k x A)) / (1 / (h x A)) = R_cond / R_conv = h x L / k ≡ Bi.

A_cond, the area of the exposed solid surface, matches A_conv, the area of the fluid boundary layer, so the two cancel out here (but this is not so when we go on to deal with conduction through 16.5 m² of solid refractory in two muffles whilst 2.6 m² is the effective surface area of two corpses for determining the radiative transfer rate). L and k are known variables as described above. Details of how to find h, the convective heat transfer coefficient (W/m².K), are in the section below on the calcining part of the cremation cycle.

Given the Biot and Fourier numbers, the exact solution for the dimensionless temperature at various distances is obtained from the infinite series in this summation:

θ(S, τ) = ∑_{n=1 to ∞} C_n x exp(-λ_n² x Fo) x cos(λ_n x S)

There is a one-term approximation θ(S, τ) = C₁ x exp(-λ₁² x Fo) x cos(λ₁ x S), in other words, just the first term in the series, but this is only accurate for Fo > 0.2, which in our case corresponds to about two hours. We want to know how much the surface temperature has dropped after 30 minutes or 60 minutes, so the one-term approximation is not good enough. But the first four terms produce a pretty accurate result. Some textbooks have tables for various values of Bi with the first four roots of the transcendental equation that is used to find λ_n; in other words, the actual values of λ₁ to λ₄.

S is the dimensionless distance from the hot or insulated end of the solid, so S = 0 for the midplane or the far surface of the refractory adjacent to the insulating bricks, S = 1 for the surface exposed to the fluid or the surface that is radiating energy to a cool body, and S is between 0 and 1 for any intermediate points at various depths into the solid. The exp() is e raised to a power. λ_n (the strange-looking xi character ξ is sometimes used instead of lambda), is found from the transcendental equation:
λ_n x tan(λ_n) = Bi, and the coefficient C_n is found from:

C_n = 4 x sin(λ_n) / (2 x λ_n + sin(2 x λ_n))

To find λ_n to a very high precision, various values could be inputted, and the product λ_n x tan(λ_n) compared against Bi until the difference was as low as necessary. However, that is far too time-consuming, and it was decided to write a program that would find the first four values of λ_n and C_n on demand, before going on to calculate the temperatures at various depths into the solid. When Bi = 0, λ₁ is 0, λ₂ is π, λ₃ is 2π and λ₄ is 3π. For very low values of Bi, the λ_n values are a little higher. At Bi = 1, λ₁ is 0.8603, λ₂ is 3.4256, λ₃ is 6.4373 and λ₄ is 9.5293. At Bi = ∞, λ₁ is π/2, λ₂ is 3π/2, λ₃ is 5π/2 and λ₄ is 7π/2, and for very high values of Bi, the corresponding λ_n values are a little lower. Thus, λ_n is in the range (n-1)π to nπ.

λ₁ was found by starting at λ = 0, incrementing λ, and recording λ as the result as soon as Bi - λ tan(λ) becomes negative. Each subsequent λ_n up to λ₄ was found by repeating the process starting at λ = (n-1)π. For Bi < 1, λ was incremented in steps of 0.000001; for remaining values up to Bi = 100, the incrementing was in steps of 0.00001. The maximum computation time was 20 seconds at Bi = 0.9, and the maximum diversion from the textbook values would lead to an occasional rounding up of the 4th decimal place; a difference of about 1 in 80,000. Table 5.1, p. 227 of the Third Edition, Introduction to Heat Transfer, Incropera and DeWitt, appears to have a typo in the 3rd decimal place for C₁ at Bi = 2.0; they have 1.1795 instead of 1.1785, although λ₁ (or (ξ₁) is correct at 1.0769.

(For those who want to run this program for themselves, download planewallcode.htm; copy the text and save as a .bas file. It can be run in Windows XP under QBASIC (which is where the computation time can be up to 20 seconds), or in Windows 7 64-bit under a DOS command prompt using QB64 (whereupon an .exe file is compiled, and the results are displayed with no noticeable delay).

When λ_n is known, C_n can be calculated. For example, Google: "calculator", and the following can be performed:
4 sin(1.0769) ÷ (2 × 1.0769 + sin(2 × 1.0769)) = 1.1784630718
(Note: The trig functions sin, cos and tan as used here are based on the value in radians. Some pocket calculators default to degrees and need a few extra key entries to work in radians, in which case, online calculators are useful.)

There is a one-term approximation for calculating the amount of energy transferred out of the solid, but the error is large at low values of Bi or Fo when the solid still retains much of its heat. The program used here accepted inputs of the dimensionless variables Bi and Fo, displayed the first four discrete values (eigenvalues) of λ_n and C_n (for checking against textbook tables as available), displayed 21 values of θ(S, τ) from S = 0 to S = 1 in increments of 0.05, and then displayed the proportion of energy transferred out of the solid, after calculating the temperature at 101 points from S = 0 to S = 1 in increments of 0.01 and averaging out.

That's the exact solution for the transient conduction problem of the plane wall, where the wall is subject to convection starting at time t, τ and Fo = 0. For further reading, see the links for the two diagrams above here and here. In adapting this to the problem of energy radiated from the walls to the corpses, we can consider how the Biot number is determined.

There is an analogy with the case of two resistors R₁ and R₂ in series in an electrical circuit. Where the applied voltage is V_total, the current flowing through each resistor is I = V_total / (R₁ + R₂), and the voltage across each resistor is V = I x R_n. If R₁ is half the resistance of R₂ for example, ¹⁄₃ of the voltage drop is across R₁ and the remaining ²⁄₃ across R₂. Going back to the way Bi is defined, if R₁ is the resistor at the top of the drawing, the voltage drop across that is analogous to the temperature drop across the thermal resistance of the solid in the thermal circuit when it's in equilibrium, and the voltage drop across R₂ is equivalent to the temperature drop across the fluid boundary layer. A low Bi corresponds to R₁ being a low resistance in comparison to R₂, so that the voltage at the midpoint is nearer to the supply rail than the ground, or similarly, the temperature T_s at the exposed surface of the solid is closer to the higher temperature T_i maintained at the insulated side (or the midplane) than it is to the lower temperature T_∞ of the free-flowing fluid. The electrical circuit reaches equilibrium very quickly, subject to stray capacitances in the system, whereas the thermal circuit might take days to reach equilibrium. Here's the definition of Bi again for reference:
(T_i - T_s) / (T_s - T_∞) = (L / (k x A)) / (1 / (h x A)) = R_cond / R_conv = h x L / k ≡ Bi.

Irrespective of whether or not the thermal circuit is in equilibrium, the Biot number is always equal to the ratio of the two thermal resistances, so that in the case of the plane wall with convection, it's always equal to h x L / k. In order to make it equal to (T_i - T_s) / (T_s - T_∞) as well, we have to specify that the hot side of the solid is maintained at T_i and the system is in thermal equilibrium. Before it reaches equilibrium with the heat transfer rate through the solid equalling the heat transfer rate through the fluid, the temperature drop across the solid is less than the equilibrium value so that the heat transfer rate through the fluid boundary layer exceeds the heat transfer rate through the solid, and the exposed surface of the solid cools until reaching the equilibrium temperature. At any time, q_conv = (T_s - T_∞) / (1 / (h x A)) and q_cond = (T_i - T_s) / (L / (k x A)), or in other words, the heat transfer rate is determined by the temperature difference ΔT divided by the thermal resistance, just like the electrical current is determined by the potential difference divided by the electrical resistance. One has joules per second flowing through; the other has coulombs per second.

For radiative transfer from the refractory material to the corpses, the problem is that the thermal resistance to heat transfer between walls and corpses is not constant, but is a dependent variable, determined by the first and second powers of the absolute temperatures of walls and corpses. Using the same basis to find the resistance to radiative transfer as in the case of 1 / (h x A) being the resistance to convective transfer, we have:
R_rad = (T_s - T_∞) / q_rad = (T_s - T_∞) / [A_rad x 5.67x10^-8 x (T_s⁴ - T_∞⁴)] = 1 / [A_rad x 5.67x10^-8 x (T_s² + T_∞²) x (T_s + T_∞)]

And R_cond = (T_i - T_s) / q_cond = (T_i - T_s) / [(k x A_cond / L) x (T_i - T_s)] = 1 / (k x A_cond / L) = L / (k x A_cond)

The temperature terms remain in the equation when calculating the Biot number. It doesn't matter about T_∞ because that's assumed to be constant during the evaporation, but T_s is certainly variable:
Bi = R_cond / R_rad = A_rad x 5.67x10^-8 x (T_s² + T_∞²) x (T_s + T_∞) x L / (k x A_cond)

A_rad is 2.6 m² for two corpses; A_cond is 16.5 m² for two muffles; T_∞ is the temperature of the corpses taken as 373.15 K during the evaporation phase; k is 0.767 W/m.K; L is 0.122 m; T_s is the exposed, cooler surface of the refractory, a dependent, unknown variable. For the outer refractory walls with 15 cm of refractory followed by insulating and normal bricks, the average temperature T_i after preheating is is 782 °C, which is the average of the 850 °C hot surface, and the 714 °C adjacent to the insulating bricks. The inner partition walls are all at 850 °C. There is 1.541 m³ of exterior wall, and 0.466 m³ of interior walls, so the weighted average is (1.541 x 782 + 0.466 x 850) / (1.541 + 0.466) = 797.79 °C. Let's say 800 °C. (The front was an exterior side but didn't have all the insulating bricks and normal bricks; one would hope that the outside surface wasn't too hot.) The mass of refractory (excluding insulating and normal bricks) in two muffles is 4,014 kg, and the specific heat is 930 J/kg.K.

As with the case of determining Bi with conduction / convection, with conduction / radiation we can find what T_s corresponds to the steady state when the other side of the refractory is maintained at T_i. When the system reaches this equilibrium state, q_cond = q_rad. That becomes:
(T_i - T_s) x k x A_cond / L = A_rad x 5.67x10^-8 x (T_s⁴ - T_∞⁴)

At equilibrium, T_s = 446.46 °C (719.61 K), and q_cond = q_rad = 36,674 W. This would correspond to a Biot number of 1.02; T_s is just a little below the mean of 100 and 800 °C.
Bi = R_cond / R_rad = A_rad x 5.67x10^-8 x (T_s² + T_∞²) x (T_s + T_∞) x L / (k x A_cond)

Now that's the situation by the time T_s has cooled down to that equilibrium temperature. But most of the time it's going to be hotter than that. At the higher temperatures, the heat transfer rate increases more rapidly compared to the case of convection. Whilst R_cond remains constant, R_rad decreases significantly with increasing temperature, since it's related to the first and second powers of the absolute temperatures. (In the case of convection, R_conv also decreases somewhat with increasing temperature, since the Rayleigh or Reynolds numbers would increase with temperature, and the Nusselt number and convective heat transfer coefficient h would increase with about the cube or square root of Ra or Re. But the effect is small compared to the variation in R_rad.) Thus, the Biot number is really higher than is indicated by the equilibrium temperature test.

(The exterminationist claims are actually helped by a higher Biot number, which may be counter-intuitive, because the exposed surface temperature will drop relatively rapidly with higher Biot numbers. However, the heat transfer rate turns out to be greater. Given that Bi = R_cond / R_rad, increasing Bi by decreasing R_rad, when R_cond remains constant, decreases the total resistance to heat transfer, thereby increasing the heat transfer rate.)

Where the walls of the linked pair of muffles are radiating to two corpses at 100 °C, q_rad = 2.6 m² x 5.67x10^-8 x (T_s⁴ - 373.15⁴), and when T_s is reduced in 0.1 K decrements from 800 °C down to 450 °C, the average q_rad is 100,405 W. At 1,073.15 K it's 192,665 W; at 723.15 K it's 37,457 W. The average T_s - T_∞ is 625 - 100 = 525 °C. In the convection case, q_conv = h x A_conv x ΔT, so the convective heat transfer coefficient h = q_conv / (A_conv x ΔT). Thus, an average q_rad of 100,405 W corresponds to a convective heat transfer coefficient h of 100405 / (16.5 x 525) = 11.6 W/m².K. From Bi = h x L / k, this would make Bi = 11.6 x 0.122 / 0.767 = 1.84.

We want to know how long it takes to transfer 194.25 MJ from the refractory walls of the linked pair of muffles to dispose of 75% of the water in two corpses, which includes energy absorbed by the water vapor. The excess energy contained within the walls at a temperature of 800 °C, compared to the walls at 100 °C, is 4,014 kg x 930 J/kg.K x 700 K = 2,613 MJ. Thus, the proportion of that energy needed to be transferred is 0.07434. From t = Fo x L² / α, the time t corresponding to a Fourier number of 1 is 1 x 0.122² m / 4.124x10^-7 m²/s = 36,091 seconds = 10.025 hours. Going over to the program that accepts inputs of Bi and Fo, and displays the surface temperature, the temperature at other points, and the proportion of that total excess energy transferred by time Fo, Bi is inputted as 1.84, and various values for Fo are inputted until the proportion of energy transferred is close to 0.07434. The combination Bi = 1.84, Fo = 0.05297, gives a result of 0.074341 of energy transferred at time Fo = 0.05297, which is 31.9 minutes. However, the predicted temperature of the exposed surface at that time is 0.65712 in its dimensionless form, so that's 100 °C + 0.65712 x 700 °C = 560 °C. That is not consistent with the previous paragraph's estimate of a temperature range of 800 down to 450 °C, with Bi derived from that.

After trying out a number of iterations, the correct final surface temperature appears to be about 551 °C. When T_s is reduced in 0.1 K decrements from 800 °C down to 551 °C, the average q_rad is 120,681 W. The average T_s - T_∞ or ΔT across the fluid boundary layer is 675.5 - 100 = 575.5 °C. In the convection case, h = q_conv / (A_conv x ΔT), and Bi = h x L / k, so Bi = q_conv x L / (A_conv x ΔT x k). Thus, an average q_rad of 120,681 W corresponds to Bi = 120681 x 0.122 / (16.5 x 575.5 x 0.767) = 2.02.

After inputting Bi = 2.02 and various values of Fo, the combination Bi = 2.02, Fo = 0.04888, gives a result of 0.074347 of energy transferred at time Fo = 0.04888, which is 29.4 minutes. The predicted temperature of the exposed surface at that time is 0.64411 in dimensionless form, which is 100 °C + 0.64411 x 700 °C = 550.88 °C. That is consistent with taking a range of 800 to 551 °C for T_s, as above.

If Bi is simply assumed to be 3, say, a shorter time would be predicted, but after cross-checking by taking into account the final surface temperature of 509.83 °C, and calculating the average transfer rate of 111,881 W, that corresponds to Bi = 1.943, and so it is not right. Similarly, when Bi is assumed to be 1, it takes longer to transfer the required energy, and now the final surface temperature is 613.58 °C. The average transfer rate between 800 °C and 613.6 °C is 135,554 W, which indicates Bi = 2.153.

Note how this evaporation time of 29.4 minutes, under the bold new regime of lean burn cremations with insufficient fuel to enable an auxiliary power source, is after pulling out all the stops to be as favorable as possible to the exterminationist allegations. We've assumed an emissivity of 1 so that the refractory walls can operate most efficiently as heat accumulators. Given that the emissivity is probably about 0.75, the time should really be increased by around one-third to almost 40 minutes. Similarly, we've assumed that the walls are preheated to a surface temperature of 850 °C, as opposed to the 600 °C in Professor Schläpfer's diagram. The heat transfer rate at 600 °C is only 35.7% of the rate at 850 °C. We also assume that the Sonderkommando shut off the air inlets, and reopen them, at exactly the right time. Conventional cremations that don't skimp on fuel, where a constant 850 °C was maintained, would manage a heat transfer rate of 2.6 x 5.67x10^-8 x (1123.15⁴ - 373.15⁴) = 231,731 W, and so the time to transfer the required 194.25 MJ is 838 seconds = 13.97 minutes. One can make an allowance for the emissivity if necessary, but that applies in both cases, so either way, the heat accumulator cremations, which are demanded by the exterminationist allegations given the known facts about fuel availability, would take about twice as long for the evaporation phase, compared to a conventional cremation. And that's a pretty good indicator for the rest of the cremation cycle, if it worked, that is!

Also note that in any subsequent cremations attempted - after they've preheated eight ovens and in doing so have already used enough coke to cremate nearly 500 corpses at 1.6 kg of coke per corpse!!! - the evaporations would follow after the other endothermic stage of calcining the bones at the final part of the cycle, and so the walls temperature would have already declined. Thus, every subsequent attempt at cremation would take more than half an hour merely for drying out the corpses (unless they admit failure immediately and start preheating again for another attempt from scratch, followed by the inevitable failure), before we even start to make more realistic evaluations of the emissivity, the crematorium oven operating skills of the Sonderkommando, etc.

Simultaneous cremations of multiple corpses in a single muffle - effect on evaporation time

Now we come to the topic of simultaneous cremations per muffle. And here we can do a direct comparison, with the same methodology used to arrive at the 29.4 minutes evaporation time, and see how much time is required per corpse in the simultaneous cremations scenario, as well as predicting the final refractory surface temperature.

In some deliciously loony Hoaxer scenarios - the sort that were being touted as credible by learned lawyers even as late as 2000, they allege multiple corpses stuffed in the same muffle. For example, Henryk Tauber claimed four or five corpses per muffle could be burned in 20-25 minutes (see Auschwitz: The Case for Sanity [p. 312]), which is a rate of (4.5 x 60 / 22.5 =) twelve corpses per muffle per hour. So we suppose that a pair of muffles in an eight-muffle oven has been successfully preheated to equilibrium, and then nine corpses are loaded into the muffles. The total energy requirement to dispose of 75% of the water for two corpses was taken as 194.25 MJ. So now we have nine corpses instead of two, and the energy required is 874.12 MJ. As before, the initial surface temperature of the refractory walls is 850 °C, the side against the insulating bricks is at 714 °C, and after taking into account the internal dividing walls at 850 °C and averaging everything out, the average temperature of the refractory material is near enough to 800 °C. As before, the energy that would need to be taken out of the refractory material in order to bring its temperature down to 100 °C is 4,014 kg x 930 J/kg.K x 700 K = 2,613 MJ. And now the proportion of that energy that needs to be transferred over to the corpses during the evaporation part of the cremation cycle is 874.12 / 2613 = 0.3345 (as opposed to 0.07434 before, when only 2/9 of the energy was needed).

With four or five corpses stuffed together, for radiative transfer purposes, the refractory walls are not going to see as much as 4.5 x 1.3 m² of corpse per muffle. If two corpses are side by side, and they are piled two or three deep, the top view doubles from about 0.6 m² to 1.2 m², the bottom view doubles similarly, and the two side views of 0.3 m² go up by, say, two-and-a-half times to 0.75 m². Thus, we have 1.2 + 1.2 + (2 x 0.75) = 3.9 m² compared to the 1.8 m² of one body. When the cremation expert Prof. Schläpfer used 1.3 m² as the area of one corpse as "seen" by the radiating walls, compared to the 1.8 m² actual surface area of an adult human, he was de facto using a radiation view factor of (1.3 / 1.8 =) 0.722. After multiplying the 3.9 m² by the view factor of 0.722, we have an area of 2.82 m² as seen by the transmitting walls, or 5.64 m² for the two linked muffles in the eight-muffle oven. So in calculating R_r, we take the absorbing area of nine corpses as 5.64 m² instead of 2.6 m² as for two corpses.

The final temperature of the exposed refractory surface will obviously be lower than before, since more energy has been transferred. At lower temperatures, the radiative transfer rate is lower. From Bi = R_cond / R_rad, that has the effect of lowering the Biot number. The resistance to radiative transfer has increased, whereas the resistance to conduction in the refractory remains unchanged. But this is countered by the increase in surface area of the corpses, which decreases the resistance to radiative transfer. Finding what temperature T_s corresponds to the steady state when the other side of the refractory is maintained at T_i would predict too low a Biot number, since the transfer rate is higher at higher temperatures. Nevertheless, it provides some comparison between two corpses and nine corpses. With the two corpses, from (T_i - T_s) x k x A_cond / L = A_rad x 5.67x10^-8 x (T_s⁴ - T_∞⁴), we had T_s = 446.46 °C (719.61 K), and q_cond = q_rad = 36,674 W, corresponding to a Biot number of 1.02. With the nine corpses, A_rad has increased from 2.6 m² to 5.64 m². The other independent variables are unchanged: T_i is 1,073.15 K, T_∞ is 373.15 K, k is 0.767 W/m.K, A_cond is 16.5 m² for two muffles; L is 0.122 m, there is 4,014 kg of refractory material of density 2,000 kg/m³, specific heat of 930 J/kg.K., and thermal diffusivity α of 4.124x10^-7 m²/s. And the equilibrium T_s with the hot side of the refractory maintained at 800 °C is 361.05 °C (634.2 K). This would correspond to Bi = 1.68, but it's really more than that.

With two corpses in the two muffles, the walls' surface temperature dropped to 551 °C. Let's start by supposing it drops to 500 °C with nine corpses in the two muffles. A_rad is adjusted up to 5.64 m², and the average heat transfer rate over the 800 to 500 °C range is 238,395 W. From Bi = q_conv x L / (A_conv x ΔT x k), and in this case ΔT is the average T_s - T_∞ of 650 - 100 = 550, so Bi = 238395 x 0.122 / (16.5 x 550 x 0.767) = 4.178. When we input Bi = 4.178 along with various Fo values until the proportion of energy transferred is the required 0.3345, the combination Bi = 4.178, Fo = 0.2033 predicts 0.33454. However, the dimensionless T_s is 0.2675, which works out as 100 + 0.2675 x 700 = 287.25 °C, which is not consistent with the temperature dropping to 500 °C and the average transfer rate between 800 and 500 °C.

After several iterations, the result converges on the exposed refractory surface dropping to 304 °C, for which the average radiative transfer rate between 800 and 304 °C is 169,114 W. Bi = 169114 x 0.122 / (16.5 x 0.767 x 452) = 3.607. Going over to the program for finding the temperature at various depths into the refractory material, with inputs of Bi = 3.607, Fo = 0.2205, the proportion of energy transferred is computed at 0.33448, and the exposed surface temperature is 0.2912, which is 100 + 0.2912 x 700 = 303.84 °C.

(At the other end of the refractory, where the dimensionless distance is 0 rather than 1, the dimensionless temperature is 0.8601 (702 °C). And sticking with Fo or τ at 0.2205 and looking at the temperature at various depths into the refractory, for S = 0.25, θ(S, τ) = 0.8234 (676 °C). For S = 0.5, θ(S, τ) = 0.7131 (599 °C). And for S = 0.75, which is 3.05 cm into the 12.2 cm thick (on average) refractory material from the exposed end, θ(S, τ) = 0.5317 (472 °C). The thermal gradient is steeper at the cooler, exposed end. In the diagram above - their "Figure 5.4" - the curve is between the Bi = 1 and Bi >> 1.)

The time taken, and this is just for the evaporation phase of the cycle, is 36,091 seconds x 0.2205 = 7,958 seconds = 132.6 minutes for nine corpses in two muffles, which is 1,768 seconds or 29.47 minutes per corpse per muffle. The Fo number for one corpse per muffle was 0.04888, and 36,091 seconds x 0.04888 = 1,764 seconds or 29.40 minutes. Thus, the time for simultaneous cremations is four seconds longer per corpse per muffle. Simultaneous cremations do not provide any savings in time, and claims of twelve corpses per muffle per hour are outrageous lies. If there really had been a "Holocaust", one has to ask why so many proven liars have crawled out from under it.

Even if the brave new system of cremations without auxiliary power worked (and it would certainly fail at the calcining stage), the time for cremations would be significantly increased compared to the one-hour cycle that might be possible with the conventional way of operating cremators that consumed 20 or 30 kg of coke per corpse. Given that the one-hour cycle already requires that the ovens were running for 42 (forty-two) hours per day, the negligible fuel strategy with bodies that supposedly burned of their own accord would require operation for much more than that. Thus, the impossibility in terms of time becomes even more impossible, before we even start to count the other physical impossibilities, the logical absurdities, the lying "eyewitnesses", the millions of "survivors", the multiple claims of "six million" Jews facing extermination years before Hitler and the "Nazis" came to power, the supposed need for Zionist political activists to have their own country because the Jews were allegedly hated for no reason at all in the Victorian era before Hitler was even a teenager, etc.

The fats' flash point or melting point is 184 °C, and auto-ignition point is 280 °C. Thus, the first attempt at cremating four or five bodies per muffle might get to the fat-burning stage, provided the refractory material started at 800 °C immediately after preheating, and the Sonderkommando closed and opened the inlets at the correct time. However, at 304 °C, the final surface temperature is only 24 degrees above the auto-ignition temperature. After the first round of 36 corpses in eight muffles fails at the calcining stage, following preheating of all the ovens with an amount of coke that was supposed to cremate almost 500 bodies, the initial refractory temperature T_i is hardly going to remain at 800 °C after the endothermic stage of attempting to calcinate the bones.

For example, if the refractory material averaged 605 °C at the start of evaporation for a subsequent batch of corpses, the average transfer rate between 605 °C and 280 °C is 86,400 W, and so Bi = 86400 x 0.122 / (16.5 x 0.767 x 342.5 = 2.432. (The 342.5 is the difference between 100 and the mean of 280 and 605.) At Bi = 2.432, Fo = 0.2802, the proportion of energy transferred is sufficient at 0.33454, and the dimensionless T_s is 0.3566 which is 100 + 0.3566 x (605 - 100) = 280.08 °C, close enough to the 280 °C lower limit assumed in the transfer rate range. So any starting temperature below 605 °C would take the walls' surface temperature down to below the fats' auto-ignition temperature, and there would be increasing problems with ignition at decreasing temperatures. And for a starting refractory temperature of 605 °C, the evaporation time has lengthened to 36,091 seconds x 0.2802 = 10,113 seconds, which after dividing by 4.5, is 2,247 seconds = 37.45 minutes per corpse per muffle.

In the case of one corpse per muffle, the evaporation time would lengthen similarly for any subsequent attempts to cremate, starting from a lower refractory temperature, before the Germans would inevitably conclude that the bold new heat accumulators cremation method was not going to be successful. But with multiple cremations, on any subsequent batches, it is very probable that evaporation would take the walls surface temperature down to below the fats' auto-ignition point, and thus would present a new set of problems with ignition, possibly requiring multiple opening of the muffle gate to facilitate forced ignition of the corpses.

Even with one corpse per muffle, assuming no ignition problems and no requirement to open the muffle gate until after the process has completed, temperatures of the refractory surface will still fluctuate by at least 300 degrees Celsius with every single cremation. With simultaneous cremations of multiple corpses per muffle, the fluctuation would be at least 550 degrees. All the massive cooling and heating of refractory material in the bold new process of cremations with cold air and no auxiliary heat source, is hardly conducive to preventing cracks and achieving cremation engineer Rudolf Jakobskotter's proudly stated upper limit of 3,000 cremations before the brickwork needed replacing. And experts who have studied cremation such as the professional engineer Chris H. Beek, P.Eng., recognize that "When the charging door is opened during or after the process, large amounts of cold air rushes in, chilling the surface layer of the refractory material and ultimately leading to stress cracks."

At 3,000 cremations per muffle, 156,000 corpses can be cremated, in line with the number who actually died at Auschwitz-Birkenau from natural causes such as typhus and malnutrition. The Hoaxers' conspiracy theory requires 1,300,000 / 52 = 25,000 cremations per muffle. If the Germans really had been sufficiently crazy as to attempt cremations with negligible fuel, and if we forget about the fact that the process wouldn't have worked anyway, the increased wear and tear on the refractory material alone would have meant that it was not even possible to cremate those who died from natural causes, let alone those who were allegedly "exterminated"!

Determining the gas flow rate though the muffles

And this brings us to the topic of the stack flow rate. Even during the endothermic stages of the cremation cycle - the initial evaporation phase, and the final calcining of the bones - the air would be heated, partly by convection and the hot refractory walls surface, and to some extent by the water vapor in the atmosphere absorbing the infra-red radiation given off by the walls. This would inevitably bring about some flow of air through the oven, if the inlet doors happened to be open during evaporation, or when they were open as they had to be during calcination, unless the Germans inexplicably intended to end up with thousands of tons of black, charred bones that were difficult to crush, including 2.6 million thigh bones, 1.3 million skulls, 31.2 million ribs, etc., plus ~40 million teeth, and would have made Auschwitz-Birkenau look like a coal mine. It's interesting to find what the flow rates would be during the periods when the only heat source was the refractory walls.

The buoyancy of warm or hot gases in the chimneys would have determined the air throughput for the eight-muffle Topf ovens, which were not equipped with any blowers, and had only a single damper for the exhaust from each set of four muffles. The Germans would have been unable to control the flow rate in individual muffles, and if the gate valve had been carefully set up to some optimum adjustment that gave best results throughout the cremation cycle, they would not want to have to keep adjusting it. The standard type door in the gasifier would be closed, since the brave new cold air cremations system with its mandatory 95% fuel reduction target meant that the Germans could not afford to run the gasifiers except for preheating the ovens. However, the standard door in the ash chamber and the large door next to the muffle gate had to be either open or closed; any Sonderkommando who tried to hold them part-open (say, for thirty minutes or more during the calcining!) would be badly burned. The standard doors were 108 x 126 mm and weighed 7.5 kg; the large doors were 14.5 kg, and so assuming the same thickness, their other dimensions were (√1.933 =) 1.39 times that of the standard doors. A probable size would be 150 x 175 mm. Given that these combustion air feeding doors were cast-iron, which has a density of 7,150 kg/m³, and the weight of the doors was 551 kg/m², the thickness was ~77 mm.

The thermal conductivity of cast-iron decreases with increasing temperature; at 400 °C it's around 45 W/m.K, whereas at 800 °C it's in the region of 30 - 40 W/m.K. If one of these large size doors was initially at 20 °C on the outside whilst the oven interior was at 850 °C, the heat conducted through it would be at a rate of q = 45 W/m.K x 0.15 m x 0.175 m x 830 K / 0.077 m = 12.73 kW. As the outside surface rises in temperature, the conduction rate decreases until it matches the heat radiated from the door's outside surface into the oven room. This occurs at 726.4 °C when the conduction rate is (35 x 0.15 x 0.175 x (850-726.4) / 0.077 =) 1,475 W and heat is radiated into the oven room at a rate of (0.15 x 0.175 x 5.67 x 10^-8 x (999.55⁴ - 293.15⁴) =) 1,475 W = 5.31 MJ/hr = 0.27 kg of coke at 65% oven efficiency. When the door is open, the full 850 °C is radiated out into the oven room, so the rate increases to (0.15 x 0.175 x 5.67 x 10^-8 x (1123.15⁴ - 293.15⁴) =) 2,357 W.

As Mattogno informs us, the Topf ovens at Auschwitz-Birkenau not only had no recuperator to preheat combustion air, they had no instruments for controlling the combustion such as "electric pyrometers, spent gas analyzers, or pressure gauges for measuring the draft in the chimney". In contrast, modern gas cremators can monitor the condition of the cremation with thermocouples and modulate the burners as required in the interests of fuel economy and avoidance of lengthy cremation times. One example is "fully automatic" with "PLC based controls", and has a "modem link" for "remote technical support" and "on line fault diagnostics". Excluding the 8.75 kWh electricity usage, and preheating of the cremator which adds up to another 5 m³ of natural gas per cremation, it consumes 20 m³ of natural gas per cremation, which is described as "excellent fuel economy". Taking their figure of a net calorific value as > 34.82 MJ/m³, that's ~700 MJ, and equivalent to ~36 kg of coke per corpse at an oven efficiency of 65%. This is a far cry from 1.6 kg of coke per corpse!!!

Nowadays, there are simulators available that can be used in training new operators to handle process heaters so as to optimize thermal efficiency and heat transfer. The Sonderkommando would have just been informed of the importance of operating the ovens with sufficient coke if they wished to avoid the fate of their predecessors who'd experimented and failed on the job.

The volumetric flow rate in a combustion chimney - e.g. from a furnace or oven - is approximated by:
Q = Cd x A x √[2 x g x H x (T_i x M_o - T_o x M_i) / (T_o x M_i)]
...where: Q is the flow rate in m³/s, Cd is the discharge coefficient (typically assumed to be 0.65), A is the cross-sectional area of the chimney (m², e.g., 0.64 m² for Birkenau crematoria IV and V) , H is the height of the chimney (m, e.g., 16.87 m for crematoria IV and V), g is the gravitational acceleration (e.g., 9.81008 m/s² at Katowice, say 9.81 m/s²), T_i is the temperature of the exhaust gases in the chimney (K), T_o is the external air temperature (K), M_o is the molecular weight of the outside air (i.e., 28.97 g/mol), and M_i is the average molecular weight of the flue gases (g/mol).

(Here, T_i denotes the "inside" or interior temperature of the gases as opposed to T_o the "outside" air temperature; in the above section on the plane wall, T_i is elsewhere the "initial" temperature of refractory material. The usage should be apparent from the context.)

For many purposes, we can neglect differences in molecular weights and simplify to:
Q = Cd x A x √[2 x g x H x (T_i - T_o) / T_o]
...because a typical mix of CO₂ and H₂O products along with nitrogen in the combustion air will have a MW similar to that of air. For example, for a stoichiometric
C + H₂ + 1.5O₂ + 5.661 N₂ ===> CO₂ + H₂O + 5.661N₂
the products have an average molecular weight of 28.80 g/mol, compared to 28.97 g/mol for air. After averaging out for the hydrogen-carbon balance in the corpse's fats, proteins and carbohydrates, the combustion products should be mostly comprised as below:
C + 0.979 H₂ + 1.489 O₂ + 5.619 N₂ ===> CO₂ + 0.979 H₂O + 5.619 N₂ + 630.272 kJ

The average MW of the products is (44.009 + 0.979 x 18.015 + 5.619 x 28.014) / 7.598 = 28.83 g/mol, barely any change from the equal mixture of C and H₂. And any excess combustion air brings it closer to 28.97 g/mol. Even CO from a lack of combustion air has a MW of 28.01 g/mol. For the crematoria IV and V chimneys, at T_o = 281 K and T_i = 1,123 K, setting M_i at 28.97 g/mol predicts a volume flow rate of 13.10096 m³/s , which is an error of -0.3223% compared to the predicted 13.14332 m³/s at 28.83 g/mol for M_i. When T_i = 323 K and M_i = 28.97 g/mol, the predicted flow rate is 2.925983 m³/s, which is 1.817% below the prediction of 2.980118 m³/s for M_i = 28.83 g/mol.

(To recap, from our description of the Topf eight-muffle oven above, also q.v. Auschwitz: The Case for Sanity, each gasifier fed a linked pair of muffles; the carbon monoxide produced by the gasifier would burn to completion on entering the first muffle at the gasifier neck in the muffle's sidewall, flow into the second muffle, flow out into a duct that merged with another duct from another muffle-pair, with the exhaust gases from four muffles flowing into a chimney that had a square cross-section of 0.8 m x 0.8 m and a height of 16.87 meters. So given that one chimney served four muffles, when we're considering the conditions in a particular linked pair of muffles, it's going to be half the flow rate through the chimney when all four muffles are at the same stage in the cremation cycle. If the cremations in the particular muffle-pair under consideration are in an endothermic stage, whilst the corpses in the other two muffles are burning fats, the flow rate in the endothermic cremations would be higher than expected, increasing losses at the calcining stage, or if the inlet door was open during initial evaporation. It would also be higher than expected - the full rate instead of half the flow rate - if the other two muffles were not in use, but given that the Germans already need to have the ovens working about a hundred hours a day to keep up with Hoaxers' allegations, that's not very likely.)

There is a variation of the formula that's widely circulated and divides by T_i instead of T_o; it's used in calculating natural ventilation flow rates in buildings where there is relatively little difference between the inside and outside temperatures. And in a domestic chimney where the chimney height is barely more than the house's height, the temperature inside the house is warm in relation to the outside, and the chimney is partly surrounded by the warm air in the house, the house itself could provide more draft than the chimney; the warm air in the house is part of the "outside" air as far as the chimney is concerned. The Auschwitz-Birkenau chimneys were much taller than the buildings, and so the exterior air really is the cold outside air.

The above formula for volumetric flow rate, Q = Cd x A x √[2 x g x H x (T_i x M_o - T_o x M_i) / (T_o x M_i)], derives straight from Archimedes' principle. The hot gases in the chimney experience a buoyancy force equal to the weight of gas displaced, equal to
F_u = g x H x A x P x M_o / (R x T_o)
where P is the pressure (e.g., 101,325 Pa), and R is the gas constant 8.314 J/K.mol. At the same time, the hot gases experience the regular force of their own weight, equal to
F_d = g x H x A x P x M_i / (R x T_i)
The difference between these two forces, F_u - F_d, the net force acting on the hot gases in the chimney, is divided by the mass of the hot gases in the chimney, which is
H x A x P x M_i / (R x T_i)
and this obtains the acceleration a = g x (T_i x M_o - T_o x M_i) / (T_o x M_i)
This acceleration a is then inserted into V_f = √[2 x H x a] to get V_f = √[2 x g x H x (T_i x M_o - T_o x M_i) / (T_o x M_i)]
where V_f is the final velocity the hot gases would attain if they were instantly heated to Ti whilst stationary and then accelerated over the height (or length) of the chimney whilst experiencing the net force acting on them. Finally, the velocity is multiplied by a discharge coefficient, and multiplied by the area of the chimney to obtain the volume flow rate Q.

To find the natural draft pressure dp in Pa, it's dp = g x H x (ρ_o - ρ_i), where ρ_o and ρ_i are the densities of the outside and inside air respectively (kg/m³). The draft pressure is just F_u - F_d, the difference between the forces acting on the gas in the chimney, divided by the chimney's cross-sectional area, which is verified by the fact that each density ρ_n = P x M_n / (R x T_n). To find the natural draft pressure dp in mm of water column instead of Pa, it's the value in Pa divided by g, which is dp = H x (ρ_o - ρ_i). With outside temperature of 10 °C, inside temperature of 850 °C, and chimney height of 16.87 m, the natural draft is 15.73 mm-H₂O. In the experimental data quoted by Mattogno, a draft of around 15 mm of water column in a crematorium oven with a coke-fired gasifier would burn the coke on the hearth grid at a rate of about 135 kg/h per m² of grid, so the regular 35 kg/h would correspond to about 0.26 m² of coke on the grid. Now if the "Nazis" had wanted to burn the coke continuously at a rate of 3.2 kg/h per gasifier, and the draft was 15 mm of water column, they would need to use (3.2 / 35) * 0.26 = 0.024 m² of coke. Instead of having 0.51 m by 0.51 m (20 in by 20 in) of coke, they would need 0.155 m by 0.155 m (6.1 in by 6.1 in). How often do you see a real fireplace that is less than half the width of a laptop screen? And, depending on the "eyewitness", this was supposedly capable of cremating two corpses in an hour or less!

Another problem, as we shall see, is that the air flow rate through the gasifier needs to be considerably restricted by the resistance of the hearth grid and the layer of coke above it. As Mattogno says, "The highest resistance the combustion air encountered was, in fact, the resistance of the hearth grid and the layer of coke above it." That resistance needs to be in place because otherwise, given the relative size of the air inlet doors, the chimney draft would pull in too much combustion air through the gasifier, there would be an excess rather than a scarcity of oxygen, the semi-direct heating would have reverted to wholly indirect, and the oven efficiency would have plummeted. Since each muffle had a large door plus a standard type door for the ash chamber, and the gasifier had a standard type door, and the large doors were about twice the area of the standard doors, then if there was no layer of coke to resist the flow, each large door would pull in some 2/7 of the flow exiting the second muffle, each standard door would pull in 1/7 of that flow, and the flow through the gasifier at 1/7 the flow rate of the exiting gases would be too great for the required scarcity of oxygen. Now, if they decide to restrict the layer of coke to an area of 0.024 m² instead of 0.26 m² on the grid, the flow would greatly increase. However, apart from that, the 3.2 kg/hr of coke policy would still inevitably have required modifications to the gasifiers in order to restrict the combustion air in accordance with the decline in coke consumption.

So that's the correct formula, but the value of the discharge coefficient is an approximation, and before describing how the cremations would fail at the calcining stage, we want to look into how the major and minor losses would affect the flow rates. The higher the flow rate, the more energy needed to heat the combustion air. The lower the flow rate, the greater the probability that there would be insufficient combustion air during the most intense periods of burning, e.g., fat burning.

The following chart shows the predicted gas flow rates in m³/s for a linked pair of muffles in the Topf eight-muffle ovens at crematoria IV and V; i.e., it's the predicted flow rate from the above formula for the volume flow rate in a combustion chimney divided by two. The outdoor temperature T_o is taken as 8.2 °C (281.35 K), which is the mean annual temperature for Katowice, Poland. Another column shows the number of moles of gas flowing per second, which is useful when considering burning rates. The molar flow peaks at around 300 °C, since with further temperature increases the expansion of the gas dominates rather than the increase in volume flow. These values assume the outside air and the exhaust air to have the same molecular weight (28.97 g/mol), so it's the same as predicted by
Q = Cd x A x √[2 x g x H x (T_i - T_o) / T_o]. This would be correct for the lower flow rates at lower temperatures during the endothermic phases of the cremation cycle; if an allowance is made for a lower MW in the exhaust products at the higher temperatures when combustion is occurring, the flow rate would be marginally higher than as shown below at those temperatures. Of more interest is the flow rate during the endothermic stages - evaporation, and calcining of the bones, since this is when the cremations would ultimately fail. Failure would generally occur at the calcining stage, unless they were doing something crazy such as stuffing five corpses into the same muffle, in which case the refractory temperature would decrease so much that there would be a serious risk of failure to evaporate enough water and progress into fat burning.

StackFlowEightMuffle photo StackFlowEightMuffle_zps76a8fde9.png

Table 3

Of the major and minor losses, the biggest pressure drop is likely to be from the resistance to the gases flowing up through the chimney, since the pressure drop is directly related to the length of the pipe or conduit. Let's calculate the draft according to Dr = g x H x (ρ_o - ρ_i), and see how much of that is lost due to the frictional losses in the chimney. At T_o = 281.35 K and T_i = 1123.15 K, the densities ρ_o and ρ_i are 1.255 kg/m³ and 0.314 kg/m³ respectively. (For a quick calculation, use ρ_n = 353.065 / T_n. The 353.065 is from P x M_n / R, where P is 101,325 Pa, M_n is 0.02897 kg/mol, and R is the gas constant 8.314 J/K.mol.) So given the ambient temperature averaging 8.2 °C and exhaust gases temperature of 850 °C, and the 16.87 m tall chimney, the natural draft works out at 9.81 x 16.87 x (1.255 - 0.314) = 155.7 Pa. Divide by g, or remove the g in the formula, and the draft is 15.87 mm of water column.

If T_i = 303.15 K (just 30 °C), then ρ_i becomes 1.165 kg/m³ and the draft is 14.9 Pa or 1.52 mm of water column. To convert back to the flow rates, the velocity in m/s is:
V = Cd x √[2 x Dr x R x T_i / (P x M_i)], where Dr is the draft (Pa). Or it can be simplified to V = Cd x √[Dr x T_i / 176.533]. Then, dividing by two to allow for two pairs of muffles per chimney at crematoria IV and V, and multiplying by 0.64 m², gives the volumetric flow rate through one pair of muffles in the eight-muffle oven, as in the table above. It is seen that the massive reduction in draft, from 850 °C to 30 °C, does not translate into quite as large a decline in the flow rate, since even though T_i is a factor, the volumetric flow rate is proportional to the square root of those two variables. And given the higher density at low temperatures, the mass flow rate shows a much smaller decline.

The "major loss" in draft pressure due to friction in the pipe or duct is given by P_loss = λ x ρ x ½ x V² x L / Dh, where λ is the D'Arcy-Weisbach friction coefficient, L is the length of the pipe (e.g., 16.87 m for the crematoria IV and V chimneys), Dh is the hydraulic diameter (m), ρ is the fluid density (kg/m³), and V is the fluid velocity (m/s). At 303.15 K the density of the chimney gases is 1.165 kg/m³, and the velocity (before any correction for the major loss) is initially calculated (from V = Cd x √[2 x g x H x (T_i - T_o) / T_o]) at 3.292 m/s. (That's before dividing by two for the flow in one pair of muffles, and before multiplying by the area 0.64 m² to get the volume flow rate). The hydraulic diameter for the 0.8 m square chimney duct is 0.8 m, the length of one side.

The friction coefficient λ is found either by solving the Colebrook equation, or by consulting a Moody Diagram. (D'Arcy-Weisbach's friction factor is not to be confused with the Fanning friction factor, which is a quarter the value of the former.) In the Colebrook equation, the friction coefficient appears on both sides and so the solution is by "iteration", e.g., program in the known variables, and adjust the friction variable until it balances. The Colebrook equation is:
1 / λ^0.5 = -2 x log₁₀ [2.51 / (Re x λ^0.5) + (k / Dh) / 3.72] where Re is the Reynolds number, k is the absolute roughness of the pipe or duct surface (m), and Dh is the hydraulic diameter (m). Dh is 0.8 m as before, and the absolute roughness could be up to 5 mm, e.g. for "rough brickwork ducting". Note that k / Dh is the relative roughness ε, which appears on the right-hand side in Moody Diagrams. So taking 0.005 m / 0.8 m, the relative roughness is 0.00625. The Reynolds number can be calculated from:
Re = V x Dh / ν, where V is the fluid velocity (m/s), Dh is the hydraulic diameter (m), and ν is the kinematic viscosity of the fluid (m²/s). (For those unfamiliar with some of these Greek characters, nu (ν) used for kinematic viscosity, frequency, etc., is rather similar to a "v". Rho (ρ) isn't so bad, but is still a bit like a "p".)

So in our case of the 0.64 m² by 16.87 m chimney connected to four muffles from an eight-muffle oven, with the exhaust gases at 303.15 K, the velocity is initially calculated at 3.292 m/s, Dh is 0.8 m, and the kinematic viscosity ν (for dry air at 303.15 K) is 1.598 x 10-5 m²/s. Thus, the Reynolds number Re is 164,806. When the values are plugged into the Colebrook equation, the D'Arcy-Weisbach friction factor λ comes out as 0.0329737094150067, say 0.033. Compare that with a Moody diagram, where the given variables are relative roughness of 0.00625 and Re = 164,806; the friction factor is seen to be in the order of 0.033.

Now we have all the values to solve P_loss = λ x ρ x ½ x V² x L / Dh, and P_loss works out at (0.033 x 1.165 x 0.5 x 3.292² x 16.87 / 0.8 =) 4.393 Pa, which is 29.5% of the original 14.9 Pa draft. Since for a given temperature, the flow rate is proportional to the square root of the draft, the flow velocity for Dr = 10.507 Pa only decreases by 16.13% to 2.761 m/s. Moreover, since the pressure drop is proportional to V², the lower velocity reduces the pressure drop, thereby increasing the draft and increasing the velocity compared to the initially expected decline. After successive iterations, the flow velocity converges at 2.8937 m/s, a 12.09% reduction from the original 3.2917 m/s, and the draft converges on 11.541 Pa. (A program that in turn computed revised velocity and draft took eight iterations to converge to within five figures of its final 16-figure result, and 28 to reach that final result.)

The percentage reduction in draft, and velocity after we allow for a lower pressure drop due to the lower velocity, works out around the same for T_i = 850 °C. Although the velocity is higher, this is balanced out by the lower density of the gases.

Another "major loss" would arise from the length of horizontal flue duct. In Crematoria II and III, for example, furnaces number 3 and 4 had the shortest flue ducts at 6.5 and 10.5 m respectively. Whatever the parameters were of the Crematoria IV and V ducts, from the formula for P_loss it is seen that the loss in draft is directly proportional to the length, but any reduction in the pipe cross-section will considerably increase the loss by increasing the velocity. For example, if the length of horizontal duct was the same as the vertical length of the chimney, but the cross-section was only 0.6 m by 0.7 m as in the Crematoria II and III horizontal flue ducts instead of 0.8 by 0.8 m, the gas velocity increases by 0.64 / 0.42 = 1.524 times. The P_loss increases in proportion with the square of the velocity, which is 2.322 times. It also increases by 0.8 / 0.64615 = 1.238 times, because the hydraulic diameter has been reduced from 0.8 m to 0.64615 m. It also increases by 0.035112 / 0.032974 = 1.065 times, which is the increase in the friction coefficient λ due to the increased relative roughness that results from the reduced hydraulic diameter. Thus, if the horizontal duct cross-section is reduced to 0.6 m by 0.7 m, not much smaller than the 0.8 m square of the vertical duct in the chimney, the length would need to be no more than 16.87 / (2.322 x 1.238 x 1.065) = 5.510 m in order for the pressure drop across it to be no more than the 4.393 Pa introduced by the chimney.

A possible bottleneck in the flow is the openings in the sidewall between the two muffles in the linked pair, that let the gases pass from the first to the second muffle. If we allow 3 m³ as the volume of the two muffles, and (2 x 0.7 =) 1.4 m as the distance from the side of the first muffle to the far side of the second muffle, then the gas residence time (s) is 3 m³ / Q, where Q is the volumetric flow rate (m³/s), and the velocity of the gases passing through the muffles is 1.4 m / (residence time) = (1.4 / 3) x Q (m/s). This is equivalent to a cross-sectional area of 3 / 1.4 = 2.143 m². The muffle cross-section is 2 m (depth) by 0.8 m (height) for the main chamber, so a volume greater than 2 x 0.8 x 0.7 (1.12 m² per muffle) allows extra for the ash chamber. For various temperatures, the flow velocity through the muffle is shown in the above table; it's calculated as 0.4916 m/s at 303.15 K.

In general, since V = Q / A, the cross-section of the chimney duct is 0.64 m², the equivalent cross-section of the muffle is 2.143 m², and the flue ducts of two pairs of linked muffles join before going into the chimney duct, then the muffle velocity V_m is given by:
V_m = V_c x 0.5 x 0.64 / 2.143, where V_c is the velocity of chimney gases. There is also the oddity - or error - in the design of the eight- and triple-muffle ovens in which the last oven in the linked series didn't have its own gasifier, and received the gas products from the preceding muffle or muffles. So our V_m here for the eight-muffle corresponds to the gas velocity in the final muffle; the muffle adjacent to the gasifier has a lower flow rate that excludes the combustion air entering through the final muffle's inlet and the gasification of the final muffle's corpse. The final muffle had the disadvantages of lower gas residence time, a smaller share of heat received from burning the coke, higher rates of loss through conduction, and the fact that the much greater mass of combustion air that required heating would dramatically lower the gas temperature compared to the first muffle.

We'll suppose that the interconnecting openings in the eight-muffle oven sidewall are as used in the triple-muffle oven: "three large rectangular openings of about 200 by 300 mm", and there was some 250 mm of brickwork in this inner wall. (Elsewhere we have 150 mm as the partition thickness, in order to get the correct total refractory mass. Having a high estimate here will make the pressure drop as high as possible, so we can see if it is significant in relation to that of the chimney or flue ducts.) So each of these openings has 1/3 of the muffle volume flow passing through it. Their hydraulic diameter Dh = 4A / P = 4 x (0.2 x 0.3) / (0.2 + 0.3 + 0.2 + 0.3) = 0.24 m. Since Q = A x V, then for a given Q, V varies with the inverse of A. The three openings each have an area of 0.06 m², which is 1/35.72 of the 2.143 m² effective cross-section of the muffle. However, since there are three openings, the gas velocity through each one will be the muffle gas velocity V_m x 35.72 / 3 which is 11.91 x V_m. Given the muffle gas velocity of 0.4916 m/s at 303.15 K, the velocity V_o through each opening is 5.85 m/s. (Depending on whether you start from 1.053 m³/s or 0.4916 m/s in the table above, with the rounding errors V_o ranges from 5.843 to 5.855 m/s. It's actually about 5.852. Let's say 5.85.)

The Reynolds number is Re = V x Dh / ν = 5.85 m/s x 0.24 m / 1.598x10^-5 m²/s = 87,860. We'll suppose the absolute roughness is still as high as 0.005 m, so dividing that by the hydraulic diameter 0.24 m, we get the relative roughness 0.0208. On a Moody diagram, it is easily seen that relative roughness ε of 0.0208 and Re = 87,860 corresponds to a friction coefficient λ of around 0.05. From the Colebrook equation, λ works out at ~0.0497 so we'll use that. From:
P_loss = λ x ρ x ½ x V² x L / Dh, given ρ = 1.165 kg/m³, V = 5.85 m/s, L = 0.25 m (the 250 mm depth of the opening) and Dh = 0.24 m, the pressure drop is 1.032 Pa compared to the original 14.9 Pa at this temperature and the drop of 4.393 Pa for the resistance to the gases along the length of the chimney. So the resistance to flow by the interconnecting openings is less than that caused by the surface of the chimney, and in any case the pressure drop leads to a relatively small reduction in velocity and flow rate.

Let's do the same check for 1,123.15 K. The muffle gas velocity V_m is up to 3.055 m/s, and we multiply by 11.91 to find the velocity through the openings, which is 36.38 m/s. The density of the gas, assuming MW close to that of air, is 0.314 kg/m³. Taking the kinematic viscosity of air at 14.163 x 10^-5 m²/s, the Reynolds number is Re = 36.38 x 0.24 / 14.163x10^-5 = 61,648. The Moody diagram shows that at the relative roughness ε = 0.0208, as long as the Reynolds number doesn't go below about 30,000, the friction coefficient remains around 0.05, and the Colebrook equation indicates 0.0499 for λ. Thus, the pressure drop is:
0.0499 x 0.314 kg/m³ x 0.5 x (36.38 m/s)² x 0.25 m / 0.24 m = 10.8 Pa. This is 1/14.4 of the original 155.7 Pa, which compares with the 1.032 Pa pressure drop for 303.15 K being 1/14.4 of its original 14.9 Pa.

We'll see how this compares with the resistance to flow in the muffle itself. At 303.15 K the muffle gas velocity is 0.4916 m/s, and the kinematic viscosity of the air is 1.598x10^-5 m²/s. For the hydraulic diameter Dh = 4A / P for the muffle, we allow 2.143 m² for the cross-section A, which given the 2 m depth, makes the height 1.071 m. The extra 271 mm represents the allowance for the ash chamber; the excess volume in 1.5 m³ compared to 0.8 x 0.7 x 2 m. So the muffle's hydraulic diameter is 4 x 2.143 / (1.071 + 2 + 1.071 + 2) = 1.396 m. From Re = V x Dh / ν the Reynolds number is 42,946. The relative roughness is 0.005 / 1.396 = 0.00358. The Moody Diagram indicates around 0.03 for the friction factor, and the Colebrook equation confirms it as 0.0300.

From P_loss = λ x ρ x ½ x V² x L / Dh, the pressure drop is 0.03 x 1.165 x 0.5 x 0.4916² x 0.7 / 1.396 = 0.00212 Pa, which is negligible. If that's over a length of 0.7 m, it would take (0.7 x 14.9 / 0.00212 =) 4,920 m before the pressure drop matched the draft available.

The pressure drop from various "minor losses" in the system components is P_loss = ξ x ρ x ½ x V², where ξ (lower-case xi) is the minor loss coefficient and ranges from 0 to considerably more than 1. Take the case of T_i = 303.15 K where ρ = 1.165 kg/m³ and V_m = 0.4916 m/s (or lower if allowing for major losses). The term ½ρV² comes to 0.141 Pa. Even if we deduct an allowance for major losses from the original 14.9 Pa, say, if it went down to 11 Pa, then 0.141 Pa is still only 1/78 of the remaining draft. The pressure drop across a component with a minor loss coefficient of 1 would be 0.141 Pa, and so if the minor loss coefficients summed to 7.8, the resulting loss of 1.1 Pa is 10% of the total. In order to counter the draft completely, the minor loss coefficients have to sum to 78.

At 1,123.15 K the muffle gas velocity V_m is 3.055 m/s, and the density of the gas is 0.314 kg/m³. Thus, the term ½ρV² comes to 1.465 Pa, which is 1/106 of the original 155.7 Pa, just like the 0.141 Pa loss above for a minor loss coefficient of 1 was 1/106 of the original 14.9 Pa at 303.15 K, and would be around 1/78 of the remaining draft after deducting for major losses.

A ¾ closed gate valve has a minor loss coefficient of 17, and the eight-muffle ovens had a gate valve after the point where two horizontal flue ducts had merged into a single duct. Thus, they could use that to close off the exhaust of four muffles, but could not use it to control muffles individually.

Another possible cause of the flow rate being less than that predicted from stack effect, according to the temperature at which the spent gases exit the muffle, is cooling of the gases along the length of the chimney. Beek assumes a reduction of a mere 100 °F from 1,800 to 1,700 °F, which won't significantly reduce the flow rate. Firstly, the inside surface of the chimney would have already been heated during preheating, as the oven temperature is brought up to equilibrium at 850 °C or higher. Secondly, although there is going to be some cooling towards the other end of the chimney when the gases enter the chimney at high temperatures, the opposite could apply during endothermic stages of the cremation cycle, when the air would exit the muffle at relatively low temperatures and then actually be heated by convection from the chimney's inner surface, and possibly by radiation, depending on the H₂O and CO₂ content.

In his report on cremators, Beek says (p. 30) that 'Depending on the configuration of the cremator chambers, the average pressure drop across the unit may be taken as 0.25" W.G., requiring a draft at the base of the chimney of 0.35" W.G.'. This, for 'satisfactory operation', would then provide 'a minimum draft of 0.1" W.G. at the charging door'. Beek's 0.35 inches of water gauge is 87.2 Pa or 8.89 mm of water column, which compares with Heepke's experimental data ranging from 10 mm to 30 mm water column. 0.1 inch of water column is only 2.54 mm of water column. The "gross" draft provided by the chimneys at Auschwitz-Birkenau was really well in excess of requirements, and all of these various losses from ducts and components in the system would have brought it down considerably. But even then, it's not clear whether the various losses were sufficient, and it's quite likely that the gate valves would have to have been partly turned off as well. However, as in the analysis below, it is clear that with the gate valves adjusted as required, the coke consumption could have been brought down to around 17.5 kg of coke per corpse whilst maintaining satisfactory temperatures for cremation, but at 1.6 kg of coke per corpse the cremations would inevitably fail.

So throughout the range of exhaust gas temperatures, there is always going to be air flowing through the muffle unless the air inlet door is closed, and the flow rate does not vary linearly with the temperature, but is significant even at low temperatures, such as during endothermic stages of cremation such as calcining the bones. Now we have an idea of the range of gas flow rates, we can compare the rate of carbon monoxide production from the gasifier in relation to the incoming combustion air.

The gas generation rate from the gasifier, compared to the incoming combustion air flow rate

If the Germans had conspired to operate a massive extermination program to kill millions of people, and if the conspirators had simultaneously decided to embark upon a radical novel procedure for running their coke-fired cremators so that there was no massive spike in coke consumption just as they began the exterminations, and if the extermination program together with its radical new 90%+ fuel economy drive for all ovens had been decided upon in an ethereal "meeting of minds" that supposedly accounted for the total lack of evidence for either policy, such as not even a single letter from Topf about the radical procedure and not even a single photograph or piece of film footage of a homicidal "gas chamber" (we really need to suspend all disbelief here!), the gasifiers must have been run at a massively reduced rate of coke consumption compared to the regular 35 kg of coke per hour. Since the Germans had 1.6 kg of coke per corpse if we are to believe the extermination theorists' allegations, the gasifiers that fed a pair of linked muffles in the eight-muffle oven could have been consuming coke at a rate of no more than 3.2 kg of coke per pair of muffles, or 3.2 kg of coke per hour if we take an extremely optimistic assumption (given the almost total lack of an auxiliary heat source) of one hour per cremation, and also suppose that the coke consumed in preheating was trivial in comparison.

As described above, the coke is burnt in the gasifier hearth with a scarcity of oxygen, so that the carbon monoxide does not burn to completion until arriving in the first muffle of the linked pair, whereupon it meets fresh combustion air. Let's begin by describing this process with the regular 35 kg/hour of coke per gasifier, and then consider what happens under the disputed exterminationist scenario in which coke consumption is drastically cut back by at least an order of magnitude. The weights of the reactants and products are displayed so that for any given rate of carbon burning, the required combustion air and rate of generation of products is readily found. Atmospheric gases at concentrations of around 1% or lower such as argon and water vapor are approximated as 'nitrogen'.

From the reaction:

12.011 15.999 52.862 28.01 52.862
C + ½O₂ + 1.887 N₂ ===> CO + 1.887 N₂ + 110.53 kJ

...each mole of carbon (12.011 g) produces one mole of carbon monoxide (28.01 g). The "+ 110.53 kJ " is to show that the heat of reaction evolved can either remain in the products or be released to the environment; it's an exothermic reaction. The products have lower heats of formation than the reactants, and that is balanced out by the release of energy. (By convention, an exothermic reaction is said to have a "negative" heat of reaction because the products have the lower enthalpy. Some conventions are less helpful than others.) Of course, the process wouldn't work perfectly, as some carbon would be burned to CO₂ in the gasifier, resulting in more losses there, a lower oven efficiency, and a lower rate of production of CO from the gasifier. We'll consider an exterminationist scenario in which the process does work perfectly, and we'll make the optimistic assumption of 30 MJ per kg of coke, disregarding Kessler's findings that 4.8% of the coke was incombustible slag. When the second step of the combustion has completed:

28.01 52.862 15.999 52.862 44.009 105.725
CO + 1.887 N₂ + ½O₂ + 1.887 N₂ ===> CO₂ + 3.774 N₂ + 282.99 kJ

...adding the two steps, the combustion is as described in:

12.011 31.998 105.725 44.009 105.725
C + O₂ + 3.774 N₂ ===> CO₂ + 3.774 N₂ + 393.52 kJ

(The actual mechanisms involved in the CO oxidation are from the so-called "wet" carbon monoxide combustion route, since these mechanisms involving hydrogen or water vapor have much higher reaction rates compared to the CO + O₂ ===> CO₂ + O step, even at combustion temperatures. See, for example, Yetter et al, [1991]. The chain of reactions includes O + H₂O ===> 2OH, OH + CO ===> CO₂ + H, and H + O₂ ===> OH + O. At combustion temperatures above ~1,200 K, those H, O and OH radicals dominate. Below ~950 K, other mechanisms dominate involving HO₂ and H₂O₂ radicals. Carbon monoxide oxidation will only take the "bone dry" route when moisture or hydrogen levels are below about 20 ppm, in which case it is quite hard to burn, and the auto-ignition temperature goes up from a little over 600 °C to over 800 °C. As the hot CO and N₂ exits the gasifier neck and meets the incoming combustion air in the first muffle, the water vapor in that air is nearly 10,000 ppm by volume, and the gasifier products would also contain a little hydrogen produced from the coke burning. We could assume 393.52 kJ per mole of carbon is available as the CO burns in the muffle, including the enthalpy already in the CO and N_2/ gasifier products, although that's very optimistic due to neglecting losses to the gasifier walls, and the "wet" mechanisms certainly couldn't boost the yield above 393.52 kJ per mole of carbon.)

So the design calls for each gram of carbon burned to be combined with (15.999 + 52.862) / 12.011 = 5.733 g of atmospheric air, so that the carbon burns to CO. This is exactly half the 11.466 g of air it would require to burn to completion to CO₂. However, if the carbon burns to completion in the gasifier, that is the very inefficient system of wholly indirect heating, as opposed to the improved process of semi-direct heating in which the CO burns to CO₂ in the muffle (albeit in the first muffle only, not the next!). The indirect heating is particularly inefficient because the whole 393.52 kJ/mol-carbon reaction takes place in the gasifier, and then because of the carbon dioxide's high emissivity, it gives up much of its heat to the gasifier walls rather than to the muffle walls or the corpse. If the gasifier is at 900 °C, say, at equilibrium, the CO₂ product will rapidly cool to around this temperature, and then if it drops 100 °C when flowing through each muffle, it's wasted not only all its enthalpy between ambient and 700 °C in heating the flue duct, chimney, and external environment, but also the temperature drop between the adiabatic flame temperature and 900 °C has been transmitted to the gasifier. At 900 °C the enthalpy in the CO₂ + 3.774 N₂ is 145.622 kJ; at 700 °C it's 109.674 kJ; a difference of 35.988 kJ, which is only 9.1% of the 393.52 kJ total available for heating the (two!) corpses and muffles. With this technique, cremations would require much more than 20 kg of coke per corpse; it would be nearer 100 kg!

Each g of carbon produces (393.52 / 12.011 =) 32.76 kJ/g, and each g of coke is assumed to yield 30 kJ/g; thus, each kg of coke contains (30 / 32.76 =) 915.7 g of carbon which can be combined with oxygen to form (915.7 x 28.01 / 12.011 =) 2,135.4 g of CO. (If some of the energy released came from burning a small amount of hydrogen in the coke, then that would leave less CO, and would be a little more like the totally indirect heating; the water vapor has high emissivity and rapidly radiates heat to the gasifier walls.) Thus, each kg of coke will generate a maximum of 2.1354 kg of CO in the gasifier, although in practice some would burn to completion.

The 35 kg of coke per hour is (35 x 30 / 32.76 =) 32.05 kg of carbon per hour = 8.903 g/s of carbon, and the design calls for this to be combined with (8.903 x 5.733 =) 51.04 g/s of combustion air to produce 59.94 g/s of CO + N₂; that's 20.76 g/s of CO and 39.18 g/s of N₂. On the other hand, if the available air was exactly twice as much, at 102.08 g/s, the carbon would burn to completion. In this case, since the carbon burning rate is assumed to be the same, the products are being generated at a rate of 110.99 g/s, 85.2% higher than intended.

Now we have a range of gas flow rates and velocities in the table above, from stack effect. The molar and mass flow rates are useful for considering the results over a range of flue gas temperatures. It is seen that the molar flow rate remains fairly constant at ~70-80 mol/s for any gas temperatures of 100 °C and up. Given that the molecular weight of the gases remains similar to that of air (28.97 g/mol), the mass flow rate at 70 mol/s is in the region of 2 kg/s or more. We should allow for some reduction in the gas velocity as a result of reductions in the draft from friction as the gases flow along the length of the chimney, etc., as mentioned above. The predicted reduction in gas velocity from resistance to the flow in the chimney was about 12%, so if we assume all the various pressure drops reduce the flow rate by 20% in total, then the typical 2 kg/s mass flow rate for a pair of muffles becomes 1.6 kg/s.

Each muffle had one large door next to the muffle gate and a standard type door next to the ash chamber door for the combustion air feed, whereas the gasifiers had a standard type door next to the hearth door. The standard doors were 108 by 126 mm, and the large doors were approximately twice the area of the standard doors, probably about 150 by 175 mm. Given the arrangement of these doors, if they were all open, and if it weren't for the combustion air in the gasifier encountering the resistance of the coke layer above the hearth grid, then of the 1.6 kg/s of gases exiting the second muffle into the flue duct, each muffle would be responsible for approximately 3/7 of the total; i.e., 686 g/s, and the gasifier would be responsible for approximately 1/7; i.e. 228 g/s. The quantity of gases exiting each section is the sum of the combustion air entering the section and any mass lost by the fuel - the coke or corpses.

However, the gasifier is only supposed to have a coke mass loss rate of 9.72 g/s less incombustible slag or ash, which when combined with ~51 g/s of combustion air produces approximately 60 g/s of gas products. If 228 g/s was being pulled through the gasifier by the chimney draft, it would not only be enough to burn to CO₂, but would include plenty of excess air. The difference between 60 g/s and 228 g/s might be accounted for by the coke layer's resistance to the air flow. But if the Germans decided to burn the coke at a tenth the regular rate by reducing the area of coke on the grid by 90%, that would severely disrupt the delicately tuned balance.

After deducting 60 g/s from the 1.6 kg/s of gases flowing out from the second muffle, that leaves 770 g/s of combustion air flowing into each muffle through the inlet doors. The final muffle would pull in a slightly larger share through its inlet doors because the openings in the dividing wall between the muffles resist the flow of gases and have a pressure drop across them of about 7% of the total draft.

Let's say 750 g/s for the first muffle and 790 g/s for the last muffle. Gasification of the corpses only accounts for a minority of that, and does not apply during preheating. We can also divide that 750 g/s between the large inlet door for the main combustion chamber and the standard door in the ash chamber, so 500 g/s flows in through the large door and 250 g/s through the standard door in the first muffle. Thus, the 60 g/s of hot gases flows out from the gasifier neck and meets 500 g/s of combustion air flowing in through the large door in the first muffle.

The 20.75 g/s of CO and 39.17 g/s of N₂ generated from the gasifier are at 1,308 K, and both have very similar molecular weights at 28.1 and 28.14 respectively, say an average of 28.13. That's 2.139 mol/s in total, and from V = NRT/P, the volumetric flow rate of those hot gases is 0.229 m³/s. The density of the incoming combustion air at 293 K is 353.065 / T = 1.205 kg/m³, so its volume flow rate is 0.415 m³/s. If the large door is 175 x 150 mm, then from V = Q / A the velocity of the cold air as it enters the large door inlet is 15.8 m/s, and then decelerating as it spreads out into the muffle. Similarly, if the gasifier neck has similar dimensions to the large door, then the 0.229 m³/s of hot gases divided by the large door's area of 0.02625 m² predicts 8.72 m/s as the velocity of the fuel jet immediately as it enters the first muffle.

Even with the 35 kg/hr of coke burned, there is only 20.75 g/s of CO produced compared to the incoming combustion air at 500 g/s. When we add some 39 g/s of hot N₂ gasifier product, the CO is only 3.7% of the total by mass, and about the same by volume, given that its molecular weight is similar to that of nitrogen and oxygen. If the mixture was premixed, it would be too lean to burn even after allowing for the heated gasifier products CO + N₂. According to the modified Burgess-Wheeler Law suggested by Zabetakis, Lambiris and Scott for the lower paraffin hydrocarbons, the lean limit decreases linearly with increasing temperature, going from the specified value at 25 °C, up until the point where it hits zero at the flame temperature obtained when the mixture is burned at the lean limit at 25 °C ambient temperature. (See the 129-page paper by Zabetakis, pp. 21-23 and Figures 20 and 21.) If that constant adiabatic flame temperature approach can be applied to carbon monoxide with reasonable accuracy - and experiments up to a starting temperature of 300 °C are in reasonable agreement, the CO / air mixture in the first muffle would be too cold and lean to burn. If CO is burned in air at the lean limit of 12.5% at 25 °C, the CO / air molar proportions would be:

0.682CO + O₂ + 3.774 N₂ ===> 0.682CO₂ + 0.659O₂ +3.774 N₂ + 193.0 kJ

The 193 kJ suffices to heat the products to 1,393 K or 1,120 °C; a 1,095 degree temperature increase from the reference 25 °C. For example, if the ambient temperature was at the midpoint of 572.5 °C, the expected lean limit would be 6.25%. However, the 60 g/s of CO and N₂ emerging from the gasifier at 1,308 K is much less than half of the 560 g/s total of gasifier products and incoming combustion air, and the 20.75 g/s of CO is only ~3.7% of the total.

(For carbon monoxide, the prediction would be L_t = -0.01141 T + 12.785, where T is the temperature (°C) and L_t is the lean limit (volume %) for CO at that temperature. Because of the "wet" oxidation mechanisms, the flammability limits are very sensitive to the level of atmospheric water vapor. For example, the limits widen up to 3% water vapor by volume, and narrow after that. The flame temperature would be a little lower if the water vapor wasn't approximated as nitrogen, but that's accurate enough for our purposes here.)

Since the combustion would involve turbulent diffusion rather than premixed flames, then the system could be expected to support combustion where the overall fuel / air proportions in the muffle were outside the premixed flammability limits. The combustion air is flowing through the muffle at a much higher rate than the CO gasifier product, but there is going to be a boundary layer of slow-moving air adjacent to the shared muffle / gasifier sidewall, with the velocity increasing at greater distances from the refractory surface. The gasifier products emerge at a slow velocity where friction of the gasifier neck has created another slow-moving boundary layer, but at relatively high velocity from the center of the gasifier neck. At some point in the muffle, the ratio of fuel flow to air flow would be the stoichiometric ratio, allowing combustion.

For turbulent diffusion flames, it is known that when there is too much discrepancy between the volumetric flow rates or velocities of fuel and air, a stable flame is not possible. For example, as the fuel flow rate is increased there is an increasing "liftoff" height (the distance between the points where combustion begins and where the fuel jet exits its source), and eventually "blowoff" or "blowout" occurs. Moore et al (2008) stated, "If the reaction zone moves further downstream, it eventually enters a region that can no longer support combustion due to the low fuel concentration and all reaction abruptly ceases, a condition known as flame blowout (Kalghatgi [5], Pitts [6], Coats [7], Chao et al. [8, 9]."

Dahm and Mayman (1990) conducted experiments with coaxial jets of fuel and air. (The air entering the Topf muffle from the front would be turning sideways as it encounters the sideways fuel jet from the gasifier, so that both would be flowing sideways across the muffle. Both would slow considerably as they enter the muffle, given that its cross-section is large compared to that of the large inlet door and the gasifier neck, but the issue is the ratio of fuel flow to air flow.) It is seen that at a given air velocity, there is a range of fuel velocities that supports stable combustion. If the fuel velocity becomes too low, then blowout occurs. In the example below, an air velocity of 15.8 m/s - the velocity of the 500 g/s of combustion air as it enters the large inlet door at the front - and a fuel velocity of 8.72 m/s - the velocity of the 0.229 m³/s or 60 g/s of hot CO and N₂ gasifier products as they flow through the gasifier neck - is around the limit of the "stable" region that could support combustion. If the fuel flow were to be decreased by an order of magnitude, then it would certainly be well into the "unstable" region, and blowout would occur - or ignition would not be possible to start with.

TurbulentDiffusionBlowout photo TurbulentDiffusionBlowout_zpsd7874468.png

Source: Dahm and Mayman (1990)

If the Germans suddenly decided to reduce the rate of coke burning in the gasifier hearths from 35 kg/hr to 3.2 kg/hr, the CO production would plummet from 20.75 g/s to 1.9 g/s. Even at 20.75 g/s, there are issues regarding the stability of combustion, and whether or not a significant amount of CO would fail to burn. At 1.9 g/s of CO and 500 g/s of combustion air, there would have to be serious doubt as to whether the CO could burn at all, and whether the rush of combustion air would quench any flame as surely as blowing out a candle. It's quite probable that some combustion would persist at the lower fuel flow levels, but there would be an increasing flame instability, with periodic extinguishing and re-ignition of the flame, and a reduction in the oven efficiency as a larger fraction of the carbon monoxide remained unburned.

A focus for future research, for those with facilities for simulating a Topf muffle, would be to have a fixed extraction rate (e.g. 500 g/s) determined by a pump or chimney draft in the sidewall; the incoming combustion air comes in from the front, and then varying amounts of heated CO and N₂ are fed in from the opposite sidewall, to determine the minimum rate that could sustain combustion. Or better still, coke could be burned at mass burning rates of 35 and then 3.2 kg/hr in an adjacent "gasifier", with just enough oxygen allowed for it to burn to CO.

What is undeniable is that under the 1.6 kg of coke per corpse fuel economy drive demanded by the exterminationist scenario, in which the eight-muffle oven gasifiers were restricted to 3.2 kg instead of 35 kg of coke per hour, it would have been necessary for modifications to the ovens, so that the coke would still burn with a scarcity of oxygen and produce CO rather than simply burn to completion. If there were no change to the combustion air flow rate, the more than tenfold reduction in coke burning rate would transform the oxygen-scarce gasifier into a miniature coke burner with excess oxygen, in which case the cremator would have reverted to the inefficient technique of totally indirect, rather than semi-direct, heating for the muffle. By reducing coke consumption by more than ten times, they would have reduced the heat available to the corpse and muffle by about fifty times, which would be absurd. And as mentioned above, the tiny amount of coke would decrease resistance to the combustion air flowing through the gasifier, providing an even greater excess air for the tiny quantity of fuel. Thus, it would have been necessary to build a new air inlet that was much smaller than the standard type door, in order to allow in the correct input of combustion air. The door could be opened to boost the combustion air when the coke was being ignited, but would need to be closed for preheating and cremation.

The exterminationist is forced to postulate that the decision to modify the ovens for the lean burn strategy was carried in an "incredible meeting of minds", and rather than reams of paperwork and correspondence from Topf about the adaptations, it was all covered up, just like the exterminationist must argue that the death books were faked to make it appear like there were only deaths from natural causes and there was no extermination of Jews, with the "Nazis" even going to the trouble of faking the death books to show more Roman Catholic than Jewish victims, and 2,584 registered deaths under the age of ten, and so on. But apart from all this supposed faking of evidence by telepathic conspirators, isn't it a little odd that neither Kurt Prüfer nor Karl Schultze testified as to how they'd adapted the ovens for the new lean burn regime? After all, Prüfer 'confessed': "I have known since spring 1943 that innocent human beings were being liquidated in Auschwitz gas chambers and that their corpses were subsequently incinerated in the crematoriums." He could have still argued that he thought the hypothetical modifications of 1942 were to save fuel on the cremations of those who died from natural causes. And Schultze, who said he thought "criminals were being killed" at Auschwitz, could have used a similar tack.

Even at 35 kg of coke per hour, that is insufficient to heat 500 g/s of air to 850 °C. There is an alternative scenario to the 500 g/s of combustion air going in through the first muffle's large inlet door, and the 1,600 g/s of gases exiting from the second muffle into the flue duct. We could suppose that this was considerably reduced by nearly closing off the flue duct gate valve. But firstly, let's look at how much excess combustion air there is with that 500 g/s of combustion air meeting the output from the gasifier. It's also required for combustion of two corpses, so it's not necessarily excess by then, but it clearly is as it meets the gasifier fuel jet. With the 35 kg/hr of coke yielding 20.75 g/s of CO and 39.17 g/s of N₂, the balance looks like this:

CO + 1.887N₂ + 4.9O₂ + 18.5N₂ ===> CO₂ + 4.4O₂ + 20.387 N₂

The reaction releases 282.99 kJ, but since the CO + 1.887N₂ is freshly heated following the coke burning, some of the 110.53 kJ/mol from that previous reaction should be included too. Let's neglect the energy lost to the gasifier walls and suppose that the entire 393.52 kJ/mol from burning the carbon to completion is available for heating the products. The CO₂ + 4.4O₂ + 20.387 N₂ can be heated to 793 K or 520 °C.

(At this point a program was written that accepted the two inputs: coke burning rate in kg/hr and combustion air mass flow rate in g/s. The formula for the reaction was generated in the form:
CO + 1.887N₂ + aO₂ + bN₂ ===> CO₂ + (a-0.5)O₂ + (b+1.887)N₂
...normalized to a constant CO + 1.887N₂ from the gasifier. Data from the JANAF tables for the enthalpies of CO₂, O₂ and N₂ at temperatures from 300 K to 3,000 K in 100 K steps was loaded into memory, and a loop running from 301 to 2,999 K in 0.l K steps compared the energy required to heat the products to that temperature with the assumed heat of reaction, which was optimistically taken as 393.52 kJ including the energy from burning the coke. Intermediate values between the JANAF data points, which are at multiples of 100 K, were calculated by linear interpolation. The temperature with the lowest absolute difference was displayed as the result. The flow rate could either represent the incoming air flowing through the large door in the first muffle and encountering the gasifier products, or the combustion air after including the inflow through the standard door in the ash chamber, plus both doors in the second muffle. Of course, the flow rate in the second muffle is considerably larger, and the gas temperature correspondingly cooler!)

In order to sustain combustion, as mentioned above, it appears that the minimum flame temperature required is in the order of 1,100 - 1,200 °C. If the flow rates of incoming air and gasifier products are such that the gases in the first muffle can only be heated to some temperature below 1,100 °C, then because of the slow-moving incoming air in the boundary layer adjacent to the muffle / gasifier partition wall, and the turbulent conditions, there will be points where the fuel-air mixture is stoichiometric and the flame is sufficiently hot. But as the combustion air flow exceeds the gasifier product generation rate by a greater and greater margin, those relatively hot pockets will be few and far between, and it is likely that an increasing amount of CO will fail to burn.

Gas temperatures available, based on the gasifier output / combustion air inlet flow rate ratio

By the time the incoming air from the other three doors has been included, the 60 g/s from the gasifier has to heat up 500 g/s and 250 g/s of air into the first muffle and 520 g/s and 270 g/s into the second muffle. Thus, at the worst point, the ash chamber in the second muffle - and note, temperatures of at least 600 °C are required to calcinate the bones in less than seven hours; considerably higher if it is to be done in 20-30 minutes - there is certainly not enough energy to heat the air even to the 520 °C of the first muffle. A coke burning rate of 35 kg/hr can heat 1,540 g/s of air to 204 °C, compared to the 520 °C for the 500 g/s before reaching the ash chamber in the first muffle. The 1,270 g/s in the second muffle before reaching the ash chamber can be heated to 240 °C.

850 °C or higher would be an optimum temperature for calcinating the bones; not surprisingly, the process takes longer at lower temperatures. Apart from recrystallizing the apatite, the calcium carbonate in the bone must be decomposed into calcium oxide and carbon dioxide, an endothermic reaction that absorbs 1.781 MJ/kg of CaCO₃. In order for calcium carbonate to outgas CO₂ "rapidly", the equilibrium pressure of CaO over CaCO₃ must exceed the total atmospheric pressure of air at 101 kPa, which requires temperatures above 898 °C. The outgassing of CO₂ will start to occur, albeit much less rapidly, when the equilibrium pressure exceeds the partial pressure of the ambient CO₂. By 550 °C the equilibrium pressure is a little above the 0.039 kPa partial pressure of atmospheric CO₂, but an oven or furnace will have a higher concentration of CO₂ and a correspondingly higher partial pressure, and so a higher temperature is required.

CaCo3EquilibriumPressure photo CaCO3EquilibriumPressure_zps5026f984.png

Source: Wikipedia

Some sources indicate that cremations might just about be possible in the 500 to 600 °C temperature range, but at a minimum time of seven hours per body. For example, "According to McKinley (1989), the body requires a minimum temperature of 500° Celsius over seven to eight hours to achieve complete calcination of the bone." These would be open-air cremations where the CO₂ partial pressure is only that of the atmosphere, and apart from the excessive time required per cremation, each corpse would require several hundred kg of wood or the equivalent in coke, given the massive losses from radiation and convection. If cremations were taking seven or eight hours per body, the ovens would still be full of partially cremated corpses by the time the next batch of bodies were dragged up from the gas chambers, and the Sonderkommando would face summary 'justice'. And rather than 42 (forty-two) hours per day (as with one-hour cremations), the ovens would have to have operated for more than 294 hours per day! Thus, 600 °C can be taken as an absolute minimum requirement, and one that would certainly not be consistent with cremation rates of one hour per corpse. This is consistent with Mattogno's figure of "700 to 600°C" as a minimum practical limit (albeit sub-optimal) for cremations that don't merely carbonize the corpse.

Now, if the coke burning rate is reduced to 3.2 kg of coke per hour as required in the exterminationist scenario, the 500 g/s in the first muffle (before counting the inlet into the ash chamber) can be heated to 77 °C, i.e., not enough to boil the water! By the time we include the other three doors and get along to the 1,540 g/s in the ash chamber of the second muffle, the energy is sufficient to heat the air to 42 °C (that's starting from the JANAF reference temperature of 25 °C; elsewhere here, the oven room temperature has been taken as 20 °C). And that's assuming that combustion is even possible at such a lean fuel-air equivalence ratio. The worst-case formula is like this:

CO + 1.887N₂ + 164.756O₂ + 622.961N₂ ===> CO₂ + 164.256O₂ + 624.848 N₂

Suppose the Germans were running the gasifier at the rated 35 kg/hr of coke and they wanted to set the combustion air flow, such that it could be heated to 850 °C. The flow would be reduced by nearly turning off the gate valve in the flue duct to reduce the draft considerably. It turns out that this would correspond to a combustion air flow rate of 263.7 g/s (61.2 g/s-O₂ and 202.5 g/s-N₂), and the reaction would look like this:

CO + 1.887N₂ + 2.579O₂ + 9.752N₂ ===> CO₂ + 2.079O₂ + 11.639N₂

In debunking the absurd notion that the ovens could successfully cremate with tiny amounts of fuel, it is desirable to try to understand why the corpses were successfully cremated with realistic amounts of fuel, and to try to pin down the dividing line between success and failure.

If the flow rate out of the final muffle is 1,600 g/s, that poses several problems. It is unnecessarily high in relation to the required combustion air, it is much too high even at 35 kg/hr of coke in the gasifier to be able to heat to 700 - 850 °C for calcining the bones, and it either needs to be assumed that the coke offered a very high resistance to air flow in the gasifier, or the gasifier would have needed another, smaller, fixed air inlet, with the standard type door being open only when the coke was being ignited. If the air couldn't flow around the 0.3 m² of coke on the hearth grid, and the layer of coke did provide a very high resistance so that the gasifier flow rate was essentially set by the coke rather than the inlet size, then this resistance would have been constantly fluctuating as the coke burned and fresh fuel was loaded. If the resistance of the layer of coke was low enough to be neglected, the gasifier with its standard type door should be providing ~1/7 of the total flow exiting the system, if all doors are open and the muffles' large inlet doors each provide 2/7 and their standard type doors for the ash chamber each provide 1/7.

If the resistance of the coke layer was not so great that the flow rate would have fluctuated wildly, and if after allowing for resistance of the coke the gasifier was providing, say, 1/10 of the total, then 160 g/s out of the gasifier is an excess of 100 g/s. It's only supposed to be producing 60 g/s of CO + N₂; 8.9 g/s from the carbon, plus 51.1 g/s of combustion air, which designs for a scarcity of oxygen so the carbon can only burn to CO. An extra 100 g/s of combustion air would not only provide enough oxygen to burn to completion to CO₂, but would include excess oxygen.

How the ovens could be used to cremate successfully at ~17.5 kg of coke per corpse

Reducing the flow rate out of the system certainly solves the problem of excess combustion air for the corpses and the coke. And it helps to achieve higher gas temperatures. But even with 35 kg/hr of coke for a pair of muffles, if both air inlets in both muffles are open, the gasifier produces too low a fraction of the total gases flowing out of the second muffle to be able to heat the gases to 850 °C in the ash chamber of the second muffle. This suggests that the standard size door for the ash chamber was opened during calcination, and the large door was opened during fat burning of a corpse in the main chamber, but both doors would not be open simultaneously.

In the case of 35 kg/hr of coke and a total combustion air into both muffles of 263.7 g/s, which is a ratio that allows heating of the gases to 850 °C, the gasifier is generating about 60 g/s and the total flow rate exiting the second muffle is 323.7 g/s. So the gasifier would be providing about 1/5.4 of that total, which would be too large a fraction to be consistent with all inlet doors being open. We can deduct the 8.9 g/s from gasifying the carbon in the coke, but that leaves 51.1 / 315.1 or 1/6.17 of the total flowing out of the gasifier, which is still too much. However, this ratio of flow rates could be consistent with closing the two large doors, so that combustion air enters via the three standard type doors; two in both ash chambers, and the one for the gasifier. With the gasifier providing less than a third of the total, that could allow for the extra resistance of the layer of coke. This arrangement would be suitable for the calcination phase.

During preheating, the same ratio of gasifier output to combustion air is required. Instead of three standard type doors open, the large door in the first muffle and the standard door in the gasifier are open; the remainder are closed. As with calcination, the area of the gasifier's standard type door is one-third the area of that standard type door plus the large door for the first muffle, and with the resistance to flow from the layer of coke, the flow rate out of the gasifier is 1/5.395 of the sum of the gasifier flow and the incoming combustion air; a fraction that can support a temperature of 850 °C. The gate valve is set for a flow rate of around 648 g/s in total, which includes the spent gases from two pairs of linked muffles, and so ~324 g/s exits the final muffle of one linked pair. The resistance of the coke layer, plus the gasifier door being half the size of the standard door leads to a scarcity of oxygen in the gasifier which just allows it to burn to CO, which then burns to completion on meeting the combustion air entering the muffle through the large door.

For the first ten minutes or so when cremations commence, the corpses are in the endothermic evaporation phase. No extra combustion air is required, and so the set up remains as per preheating; the standard type gasifier door is open (as always), and the large door in the first muffle supplies the combustion air for the CO to burn to completion.

Then fat burning begins. Certainly at this point the large door in the second muffle would need to be opened. Depending on whether the ash chamber doors are opened too, the area of the gasifier inlet to the total air inlet area is either 1/5 or 1/7. With the resistance of the coke layer, the output flow rate from the gasifier might be 1/7 or 1/9 of the total, or 1/6 or 1/8 of the maximum combustion air flow rate. Since the coke burning rate in kg/hr is 1/1.714 of the flow rate in g/s from the gasifier, the 1/8 fraction would correspond to the maximum combustion air flow rate being 13.71 times the coke burning rate in kg/hr, which can sustain a gas temperature of 538 °C (by the time the incoming air to the second ash chamber is included). At the 1/8 ratio, with a coke burning rate of 35 kg/hr generating 60 g/s from the gasifier, the maximum combustion air flow rate is 480 g/s. Even with all inlet doors open, the 538 °C would ignite fat burning, and during this period, relatively little auxiliary heat would be required.

When the cremation goes into the calcination phase and the ashes drop into the ash chamber, the muffles' large doors would be closed and the standard doors for the ash chambers open. As described above, this arrangement has ~60 g/s exiting the gasifier and 263.7 g/s as the maximum combustion air flow rate in the final muffle, a ratio of 1:4.395 or 1 to (4.395 x 1.714 =) 7.533 in terms of the maximum combustion air flowing in g/s and the coke burning rate in kg/hr, and can support a gas temperature of 850 °C in the second ash chamber, which is very good for calcination.

With coke burning rates in the region of 35 kg/hr, there could be some scope for overlap, with the next corpses introduced into the muffles before the previous corpses' bones were fully calcinated. Provided the fat was burning, high temperatures could be maintained in the ash chambers even when all inlet doors were open. However, the fat burning phase does not last as long as the calcinating phase. The amount of overlap possible would be limited, as a backlog of partly calcinated bones would pile up in the ash chamber, especially in the second muffle.

The impossibility of cremating at 3.2 kg of coke per hour per gasifier

Once the coke burning rate goes down to 3.2 kg/hr, the situation is hopeless, and burning the coke at such a low rate - if it were even possible - would be counter-productive, since the carbon dioxide would hinder calcination and, due to its significant absorptivity, would increase heat losses in the second ash chamber by absorbing heat radiated from the walls and the corpses. In contrast, the absorption with atmospheric air comprised of about 99% dry air (nitrogen, oxygen and argon) would be much lower (water vapor accounts for most of the absorption of radiant heat). There would no longer be a scarcity of oxygen in the gasifier; modifications to the ovens would be necessary, so that the air inlets were substantially reduced. Since the tiny amount of coke would take up too little an area, the layer of coke would offer little resistance to the flow of air, and so the inlet size would need to be reduced by more than (35 /3.2 =) 10.9 times. At 3.2 kg/coke per hour, the total flow rate exiting the ash chamber of the second muffle could be no greater than 24.1 g/s in order to sustain a gas temperature of 850 °C. Alternatively, it could be no more than 38.2 g/s to support a temperature of 600 °C.

The cremator designer must provide sufficient combustion air to cope with the peak heat release rates, as seen by Beek's calculation of 3,470 lb/hr for the charge, plus his additional 3,062 lbs/hr of combustion air for the natural gas. The 3,470 lb/hr alone is 1,574 kg/hr = 437.2 g/s. Beek's charge included a coffin, whereas the 'evil' "Nazis" are accused of mass murder which included the cremations of 1.3 million naked corpses at Auschwitz-Birkenau. Our estimate above concluded "376 g of air required per second". That's for a single corpse. Two corpses in a pair of linked muffles would not necessarily require twice that amount, since the fats burn quite rapidly and so peak burning in both corpses would not necessarily be simultaneous. Alternatively, if a typical "moderately thin" victim has fats amounting to 6.4 kg x 36.02 MJ/kg = 230.53 MJ, and if three-quarters of the fat burns over a period of 5 minutes, then for two corpses in a pair of muffles that's 345.8 MJ / 300 seconds = 1.15 MJ per second. Given that typical hydrocarbon combustion requires 1 g of oxygen for every 13.1 kJ of heat released, then 1.15 MJ per second requires 1,150 / 13.1 = 87.8 g/s-O₂, which requires 87.8 / 0.232 = 378 g/s of combustion air.

Of course, almost wherever you look, there is about an order of magnitude difference between on the one hand the real world of a little more than 100,000 deaths at Auschwitz, most of them Roman Catholics rather than Jews, with the deaths almost exclusively resulting from natural causes such as malnutrition and typhus as a consequence of the Allied forces declaring war on Germany and bombing supply lines, etc., years after Jewish extremists had already declared war on Germany, and on the other hand the wartime propaganda legend of a massive, invisible conspiracy by telepathic 'Nazis' to "exterminate" millions of Jews, including 1.3 million at Auschwitz, around 900,000 at Treblinka, etc., with these 'Nazis' not only successfully managing to avoid leaving any trace of material evidence such as photographs or film footage of gas chambers, written orders and a budget for the conspiracy, etc., but also somehow being capable of "psychic" powers that would enable a suspension of the law of conservation of energy, such that bodies would burn by themselves with negligible fuel.

The 263.7 g/s of combustion air mentioned above, which is capable of supporting gas temperatures of 850 °C given a coke burning rate of 35 kg/hr, would probably be a better compromise than 376 or 378 g/s of combustion air. If some fat merely pyrolyzes and fails to burn due to insufficient oxygen, that's no big deal when there is a decent auxiliary power source, whereas a lower temperature for calcination will lengthen cremation times. The flow rate out of the second muffle at 323.7 g/s includes the 60 g/s of hot CO and N₂ from the gasifier, but after air has flowed in from large and standard doors in each muffle, there is the 263.7 g/s of combustion air to be heated, and at 35 kg/hr of coke the gasifier is able to maintain a gas temperature of 850 °C as far as the second ash chamber. If the total incoming combustion air remains at 263.7 g/s whilst the coke consumption is reduced to 22.1 kg/hr, the temperature drops to 600 °C. If the total incoming combustion air remains at 263.7 g/s whilst the coke consumption is reduced to 3.2 kg/hr, the temperature drops to 123 °C. At 3.2 kg/hr of coke, the energy release rate would be sufficient to heat only 26.2 g/s of air to 800 °C, or 38.2 g/s to 600 °C.

This, then, could be the dividing line between cremation success and failure. The orthodox model has already failed because of the absurdity of the Germans ordering tonnes of Zyklon B to save their prisoners' lives at Auschwitz-Birkenau at the very same time that they were allegedly already using kilograms of Zyklon B for "liquidating" them, and because of the technical impossibility of getting 25,000 cremations per muffle when the refractory material needs replacing after 3,000 cremations and barely any of the refractory had ever been replaced, and because of the physical impossibility of running the ovens for 42 (forty-two) hours per day. It fails even at a coke consumption of 11 kg of coke per hour per muffle, because at this point the temperature in the final ash chamber has dropped to 600 °C, cremation times would have lengthened so much that the ovens would need to be operating much more than 42 hours per day, and the consumption of coke per corpse would be well over 11 kg. It fails at the available 1.6 kg of coke per corpse, because at that level cremation is not even possible.

The calcination phase of the cremation cycle

The lack of any evidence of modifications to the ovens in order to facilitate a new lean burn regime of 3.2 kg/hr of coke per gasifier hearth, and the sheer absurdity of running the ovens in that manner, rules out such a possibility. However, if the Germans had decided to use their coke merely for preheating, hoping that they could cremate from energy stored in the refractory walls, let's look at what would happen during the calcination phase.

We'll suppose that the fat burning phase has restored the refractory walls to thermal equilibrium, after cooling during the evaporation phase (and that stage alone, according to the analysis above, would have taken more than half an hour per corpse on subsequent attempted cremations!). Provided the refractory walls have been heated, the gate valve is not turned off completely, and the air inlet doors are not all closed, there will always be some flow of gases through the system due to stack effect in the chimney. Even when no coke is being burned, and when the corpses are not releasing energy, and if the air in the muffles was initially at rest apart from free convection (e.g. if the inlets had only just been opened), then the air within it will have a lower density than the exterior air outside the chimney because: (i) The atmospheric water vapor (and carbon dioxide, but there's only about 1/20th as much of it) within the muffle would absorb infra-red radiation from the walls, and conduct energy to the non-absorbing gases. (ii) The boundary layer of air adjacent to the refractory wall will absorb heat by conduction; free convection currents would start to flow within the muffle even if the gases were not flowing out into the flue duct. Once the gases start flowing out of the muffle, this layer is constantly being replaced by fresh air, and there is a convective heat transfer coefficient between the air and the walls, which is proportional to the velocity of the gases. (iii) The air in the oven room is already significantly warmer than the exterior air outside the chimney, since each muffle is transmitting kilowatts of power to the oven room by conduction through the walls, or by infra-red radiation escaping through open inlet doors, or when the corpses were loaded, which heats the floor, ceiling, walls, etc., and incoming combustion air is heated by convection.

The relative humidity for Katowice, Poland, averages around 80%, making the dewpoint 4.95 °C. Thus, assuming a typical barometric pressure of 101,325 Pa (1,013.25 hPa) or 760 mm Hg, the absolute humidity is 6.72 g/m³ and the density of the air is 1.25 kg/m³. That makes the water vapor about 0.54% of the atmosphere by mass (or 0.87 % by volume). The density of the air in the muffle at 293 K is given by ρ = 353.065 / T = 1.205 kg/m³. Taking the volume of each muffle as 1.5 m³ including the ash chamber, in one muffle the mass of air is 1.807 kg and the mass of water vapor is 9.7 g. If the water vapor is to be heated from 20 °C to 820 °C, and taking the specific heat for water vapor at 700 K as 2,080 J/kg.K, the energy required is 0.0097 x 2080 x 800 = 16,140 J.

The heat being radiated per second from one muffle's walls of area 8.25 m² after heating to 850 °C is 8.25 m² times the emissivity (we'll assume ε = 1 initially, and then consider the case of 0.75) times 5.67x10^-8 x 1123.15⁴ = 744,369 J. At around 1,123 K, the spectral peak for the radiation emitted is at a wavelength of 2.58 µm (from Wien's displacement constant divided by the temperature).

1123KRadiator photo 1123KRadiator_zps4977ddc1.png

Source: SpectralCalc.Com

For photons with a wavelength of 2.58 µm, water has a mass absorption coefficient (typically denoted by µ) of about 100 cm²/g, and a (linear) absorption coefficient (typically denoted by α) of about 100 cm^-1. The mass absorption coefficient multiplied by the density ρ gives the absorption coefficient, or in other words, α = µ x ρ. In the case of liquid water, since its density is 1 g/cm³, both coefficients are the same numerical value. Note how there is a peak around 3 µm, a wavelength at which the spectral radiance from an 1,123 K radiator is still barely off its peak value, with an absorption coefficient of more than 10,000 cm^-1. Although there is less absorption in the 1 to 2 µm region, the absorption coefficient from 3 to 10 µm is consistently greater than 100 cm^-1, and so 100 cm^-1 is a very fair value to take as the average in the range of an 1,123 K radiator.

WaterAbsorptionInfraRed photo WaterAbsorptionInfraRed_zps303a4ce1.png

Source: Wieliczka et al

(Further sources are listed at this page, or see the data here.)

For water in other forms such as ice or vapor, the mass attenuation coefficient is exactly the same as for liquid water, so we can take the value of 100 cm²/g. That must be multiplied by the density or concentration in order to obtain the absorption or attenuation coefficient in cm^-1. The water vapor in the muffle from atmospheric air has a typical concentration of 6.5 g/m³ or 6.5x10^-6 g/cm³, which is 6.5x10^-6 times the density of liquid water. Thus, the water vapor has a linear attenuation coefficient of 6.5x10^-6 g/cm³ x 100 cm²/g, which is 6.5x10^-4 cm^-1. The proportion of photons that are not absorbed by a layer of thickness L is given by:
N/N_o = e^-αL where N is the number of transmitted photons, N_o is the number of incident photons, e is 2.71828... the base of natural logarithms, α is the attenuation coefficient in cm^-1 for the substance at the wavelength(s) of interest, and L is in cm.

Therefore, for a layer of water vapor 70 cm thick (the distance between the sidewalls in one muffle) and concentration of 6.5x10^-6 g/cm³, the proportion of 2.58 µm photons that are not absorbed and are transmitted across to the opposite wall or the corpse is N/N_o = e^{(-0.00065 x 70)} = 0.95552, and so the proportion of photons that are absorbed by the water vapor is 0.04448. Alternatively, the photons might travel between front and back (200 cm) or top and bottom (80 cm, or more if they go into the v-shaped ash chamber), or even diagonally (less than 226.5 cm, since it's not a perfect cuboid). So the average path length is greater than 70 cm, although the front and back sides have a lower area, and will therefore radiate a lower proportion of photons. Sticking with 70 cm as the path length, of the 744,369 J radiated each second by the 1,123 K refractory walls, (744,369 x 0.04448 =) 33,110 J is absorbed by the water vapor. So the water vapor could be heated by 800 K in (16,140 / 33,110 =) 0.487 seconds.

(It is seen that when the corpse is being dried out at the start of the cremation, the coke or refractory walls must provide energy for heating the water vapor beyond 100 °C. When the quantity of water vapor in the muffle exceeds the amount typical of atmospheric air, the energy required to heat it increases in accordance with the mass, but the absorption or probability of photon interactions increases almost in the same proportion, so the degree of heating is primarily a function of the flow rate and the refractory walls temperature. For example, doubling 6.5x10^-4 cm^-1 to 1.3x10^-3 cm^-1 gives N/N_o = e^{(-0.0013 x 70)} = 0.91302 = 1 minus 0.08698, which is 1 minus about 1.955 as much as before.)

Interestingly, this radiative loss to the (not perfectly dry) air is inevitably present throughout the cremation cycle, as well as during preheating. Normally it is all included as part of the cost of heating the combustion air, but there's no escaping it, even in the Hoaxer scenario of a massive fuel economy drive of attempting to cremate with 1.6 kg of coke per corpse, which demands skimping by not bothering to heat the air and merely hoping that the cremations could somehow be powered from stored energy in the refractory walls. Of course, the water vapor will not all become 800 degrees hotter; the heated water molecules would conduct their heat to non-absorptive molecules such as nitrogen and oxygen, and the heating for stack flow purposes from this radiation-conduction-convection will be equivalent to more than the six degrees or so from heating all the water vapor to a temperature approaching the walls temperature. Being randomly distributed within the air, the water vapor molecules should always have plenty of adjacent non-absorbing molecules to conduct their heat to. After sufficient collisions with cold molecules, a water molecule is more than ready to absorb another infra-red photon and the process can be repeated. There would not be sufficient time for the incoming combustion air to "top out" at a temperature approaching the walls temperature (at which point these radiative losses would slow down and almost stop), since the increased temperature and reduction in density from radiative heating of the water vapor and CO₂ will cause the air to start flowing out through the flue duct and chimney (even if for some bizarre reason the air coming into the muffle had not been heated at all above the exterior temperature, and if no heat was being conducted from the refractory walls to the boundary layer of air). In order to prevent that stack flow, the gate valve would need to be completely closed, or the air inlets would all need to be closed. (Under the no-auxiliary-fuel exterminationist scenario, the air inlets might be closed for a time during the evaporation phase, but they would need to be open for calcining the bones.)

The inevitable large heat losses in the calcination phase

For a pair of linked muffles, radiative losses from the refractory walls that go towards heating the water vapor (and adjacent, non-absorbing gases) amount to 16.5 m² x 5.67x10^-8 x 1123.15⁴ x 0.04448 = 66,219 W = 238.4 MJ per hour = 7.95 kg of coke per hour (3.97 kg per muffle per hour) if the oven efficiency was 100% (which it isn't!). That's 6.11 kg of coke per muffle per hour after allowing for an oven efficiency of 65%, which compares with the 1.6 kg of coke per muffle per hour (at best, assuming one-hour cremations and neglecting preheating) that is available in the Hoaxers' legend of murderous 'Nazis' (who were substituted for the murderous Romans at Bethar alleged to have killed four billion Jews!!!!), even if it would burn satisfactorily at such a lean fuel-air equivalence ratio. That's when the oven walls are heated to 850 °C. If the wall temperature cools to 600 °C (by which time the cremations would be even more assured of failure), the rate of radiative losses from the walls decreases by a factor of 873⁴ / 1123⁴ = 0.3652. However, at the lower temperature, the wavelength of the emitted radiation increases further into the infra-red, and so the absorption coefficient increases. At 693 °C (966 K), the spectral peak is at 3 µm, which coincides with the massive peak in water absorption - where the absorption coefficient increases by more than 100-fold. And these absorption calculations are based on the minimum path length of 70 cm, so photons that take a longer path have a higher probability of absorption.

To be fair, there is an effect that could lower the rate of this heat transfer to the water vapor and subsequently to the dry air. Depending on the mass flow rate and how much the air warms up, there will be some expansion of the gases. If the temperature increase was as much as 200 °C for example - and this would be after including convective heat transfer as well, then the volume change is 293 K / 493 K = a 40.6% reduction. That is by the time it exits the muffle. The gas is expanding and going from 293 K to 493 K as it passes through the muffle(s), so on average it would have increased in temperature to about 393 K and the density would have reduced by a factor of 293 / 393 = 0.7455 times which is a 25.4% reduction. The photons emitted from the walls have about a 25.4% lower concentration of water vapor to interact with, and the absorption rate decreases by about 25.01%. This would take the 6.11 kg of coke per muffle per hour losses down to 4.58 kg of coke per muffle per hour. But the losses from convective transfer need to be added to that, even 4.58 kg of coke per muffle per hour is still well in excess of the quantity that is available to support the legend, reducing the rate of heating will reduce the temperature increase, and in any case, attempts to calcinate at 120 °C would be doomed to utter failure.

We could decide to assume 0.75 for the emissivity of the refractory walls, which would take that 4.58 kg of coke per muffle per hour down to 3.43 kg of coke per muffle per hour, which is still well in excess of 1.6 kg of coke per muffle per corpse for a one-hour cremation time. The lower rate of heating means that there isn't as much expansion of the gas, the photon absorption rate does not reduce as much, and consequently the 4.58 and 3.43 kg figures should be increased. More importantly, the lower emissivity reduces the rate of heat transfer from walls to corpse, so the evaporation phase lengthens by one-third, and during calcination the corpses are still being cooled convectively by the cold air whilst receiving less heat by radiation from the walls. The reduced heating of the corpses lengthens cremation time (if it worked!) to well over an hour, and the already increased 3.43 kg of coke per muffle per hour becomes more than 3.43 kg of coke per muffle per hour for more than an hour per corpse, well in excess of the available 1.6 kg of coke per corpse.

Thus, combining the facts that energy equivalent to considerably more than 1.6 kg of coke per muffle per hour is inevitably consumed in a partial heating of combustion air by radiative heating of atmospheric water vapor and conductive heating of adjacent nitrogen and oxygen molecules before even beginning to count numerous other energy sinks, that the exterminationist legend has only 1.6 kg of coke available per corpse (including preheating!), that the massive 95% fuel economy drive demanded by the exterminationist legend would lengthen cremation times considerably beyond an hour per corpse, and cramming multiple corpses into one muffle could not possibly provide any improvement in fuel economy or cremation time, suffices to hole Hoaxers' lies below the waterline!

During calcination, which requires a flow of fresh combustion air in order to avoid merely carbonizing the bones, there is a flow of air past the corpse in the no-auxiliary-power Hoaxer scenario because of (i) radiative heating of water vapor and conductive heating of adjacent nitrogen and oxygen, which raises the air temperature (ii) conductive heating of the boundary layer of air adjacent to the refractory walls, with the convective heat transfer coefficient increasing with increased velocity of air (iii) the incoming air is already warmer than the exterior air outside the chimney because heat from the ovens escapes into the oven room. We would like to know what is the temperature and the flow rate of this air.

It was shown above that by nearly closing off the gate valves, under conventional operation of the ovens with 35 kg of coke per gasifier per hour, there would still be sufficient air flow for combustion, and yet it would still be possible to heat the air in the ash chamber of the final muffle (by which time the air flow rate is at its maximum with air inlets from both muffles and gasification from both corpses all having merged together) to 850 °C. Let's consider the two situations: (i) There is no additional reduction of the flue gases flow rate by turning off the gate valve in the exterminationists' no-auxiliary-fuel lean burn scenario, and so the 2,000 g/s is merely reduced by 20% (e.g. by the resistance of the chimney) so that the total exiting the second muffle is typically around 1,600 g/s. (ii) The flow rate has been significantly reduced from 2,000 g/s to 323.7 g/s, a rate that at 35 kg of coke per hour per gasifier would be capable of sustaining a gas temperature of 850 °C as far as the ash chamber in the second muffle.

In the case of (i), the stack flow rate will be calculated for the particular gas temperature, divided by two to allow for one out of two pairs of muffles feeding into the particular chimney and multiplied by 0.80 to allow for a 20% reduction in flow rate resulting from various pressure drops within the system. In the case of (ii), it's as for (i), except the multiplying factor is 323.7 / 2,000 = 0.16185. In both cases the result should be arrived at by iteration. For the convective heat transfer from the refractory walls surface, increasing the temperature increases the flow rate which increases the convective heat transfer coefficient. So there is some positive feedback, although it can only go so far. (That positive feedback assumes that forced convection dominates over natural convection, which is not necessarily so, and it turns out not to be so in this case.) Moreover, the increased flow rate reduces the residence time and therefore the heating time and the temperature rise. With the radiative heating of water vapor and conduction to the dry air, there is only the negative feedback. If the air inlets and gate valve remained closed so that the air could not flow away, it would continue to heat up until it approached the walls temperature, whereas the infra-red absorption would heat flowing air by some smaller amount dependent on the flow rate. And the expansion of the gas reduces the rate of water vapor absorption.

Initially, as explained in the section above on stack flow rate, the volumetric stack flow rate is calculated from the temperature T_i by:

Q = Cd x A x √[2 x g x H x (T_i - T_o) / T_o]

...and this is divided by two to find the flow rate out of a single pair of linked muffles. The mass flow rate Q_m is obtained by multiplying by the density, and given that the gases' molecular weight remains almost equal to the molecular weight of air, the density is found by ρ = 353.065 / T. So we plug in the known variables of Cd = 0.65, A = 0.64 m², g = 9.81 m/s², H = 16.87 m, T_o = 281.35 K, and get:

Q_m = 0.5 x 0.65 x 0.64 x √[2 x 9.81 x 16.87 x (T_i - 281.35) / 281.35] x 353.065 / T_i
and so
Q_m = 79.653 x √[T_i - 281.35] / T_i

That gives the "Mass flow rate per muffle pair" in kg/s from Table 3 above. Then it is multiplied by either 0.8 or 0.16185; the latter assumes that the oven had been set up to enable gas temperatures of 850 °C in both muffles, and was not readjusted when the hypothetical extermination program and lean burn regime was introduced. It is also necessary to have the volumetric flow rate in order to find the residence time and gas velocity in the muffles (e.g. for finding the Reynolds number); the volumetric flow rate is merely the mass flow rate divided by the density, or Q = Q_m x T_i / 353.065.

(Gasification of the corpses accounts for quite a small proportion of the total flow. For example, 323.7 g/s amounts to 1,165 kg or 2,569 lb per hour. Two 55 kg (121 lb) "moderately thin" corpses - which leave a few lb of ashes, are about 10% the mass of the combustion air. Beek allowed for 3,470 lb per hour of combustion air for his charge that included a coffin, but it was one corpse rather than two. Since the exterminationist model with its 95% fuel-saving lean burn regime employs no auxiliary fuel apart from preheating, nearly all of the flow rate is accounted for by combustion air.)

The calcination phase would work best with both standard type doors open and the large doors closed. The pair of linked muffles can be considered as a single unit. The second muffle would have about twice the flow rate of the first muffle. Gas from the first muffle would travel 70 cm from side to side across the second muffle, whereas the air entering a muffle for the first time might travel halfway from front to back (100 cm) and halfway from side to side (35 cm), a typical path length of 135 cm. Thus, the average path length is 170 cm. If the volume of two muffles including ash chambers is taken as 2 x 1.5 m³ = 3 m³, then the volume divided by the volumetric flow rate gives the residence time, and the gas velocity in the muffles is the average path length of 1.7 m divided by the residence time. So the residence time is 3 m³ / Q m³/s and the gas velocity (m/s) in the muffle is 0.5667 x Q. We'll start with the case of the various losses reducing the flow rate by just 20%.

Let's forget for the moment about the lengthier time needed to dry out the corpses under the brave new lean burn regime, and suppose the initial part of the cremations proceeded satisfactorily and the burning of fats, carbohydrates and proteins have restored the refractory walls to an equilibrium state. The surface is at 850 °C and the far side adjacent to the insulating material is at 714 °C, with similar ratios between the thermal gradients as in Schläpfer's diagram, except his example has the walls at 600 °C instead of 850 °C. The temperature of combustion air entering the muffles is taken as 20 °C. Within the pair of linked muffles, the total heat radiated from the refractory walls is 16.5 m² x 5.67x10^-8 x 1123.15⁴ = 1,488,737 J/s. The water vapor content in the incoming combustion air is typically 6.5 g/m³ at 20 °C, and multiplying the 1,488,737 J/s by the previously calculated 0.04448 provides the 66,219 W as obtained above.

The combustion air entering the muffle is assumed to be at 293.15 K after being heated as it passes through the oven building, and T_i is the temperature of the gases in the flue duct and chimney after being heated in the muffles. As discussed above, in order to allow for expansion of the heated gases and a corresponding decrease in the concentration of water vapor, the 66,219 W should be multiplied by a factor of 293.15 divided by the mean of 293.15 and T_i, which is a factor of 2 x 293.15 / (293.15 + T_i). Thus, the heat transfer rate from the walls through radiative heating of water vapor is:
q_rad = 66219 x 2 x 293.15 / (293.15 + T_i), corresponding to 66,219 W at T_i = 293.15 K, 49,376 W at T_i = 493.15 K, etc.

Most of that heating transfers into conductive heating of dry air adjacent to the water vapor. Since the water vapor molecules are randomly distributed, there should be ample cold nitrogen / oxygen / argon molecules adjacent to them, avoiding cold spots of dry air where there is insufficient time to heat through conduction.

The specific heat of water vapor at 300 K is 1,864 J/kg.K and the specific heat of dry air at 300 K is 1,005 J/kg.K. The water vapor is 0.54% of the atmosphere by mass, and so each kg requires 0.0054 x 1864 + 0.9946 x 1005 = 1,009.6 J/kg.K. The average temperature in the muffle is likely to be above 300 K making the specific heats a little higher, so let's take a constant 1,010 J/kg.K. To find out the temperature rise in the air flowing through the muffles - in the ash chamber of the second muffle where the mass flow rate is at a maximum, the energy transferred to the air per second can be divided by the mass flow rate per second, and by 1,010 J/kg.K. (For this, we don't need to find the gas residence time. If it's two seconds, say, instead of one, twice the energy absorbed divided by twice as much mass flowing in that time produces the same temperature rise.)

However, the radiative transfer rate from walls to water vapor is affected by variations in temperature and density that change the concentration of water vapor. In order to prevent the calculations from becoming fiendishly complex, we'll take the rate of radiative transfer to the water vapor as a constant q_rad = 50,000 W, representing a reduction from 66,219 W, which allows for expansion as the gases are heated. (Cf. 3.2 kg/hr of coke per gasifier at 65% oven efficiency, which is 19.5 MJ/kg of coke; the heat release rate is 17,333 W.) So the temperature rise of the air ΔT = T_i - 293.15 = 50,000 / (1010 x Q_m) = 49.5 / Q_m, where Q_m is the "Mass flow rate per muffle pair" in kg/s in Table 3 above, which, without allowing for any losses due to friction, etc., is, as derived above, given by:
Q_m = 79.653 x √[T_i - 281.35] / T_i. That must be multiplied by either 0.8 or 0.16185, so for the first case we have: Q_m = 63.722 x √[T_i - 281.35] / T_i.

ΔT = T_i - 293.15 = 49.5 / Q_m, and so Q_m = 49.5 / (T_i - 293.15)

The radiative heating from the walls is absorbed by the water vapor, conducted to the dry air, and the buoyancy force pulls the air out into the flue duct and up through the chimney. As the flow rate increases, the residence time and the temperature rise decreases, and an equilibrium state should have Q_m = 49.5 / (T_i - 293.15) and Q_m = 63.722 x √[T_i - 281.35] / T_i. This is easily solved by a program that accepts inputs for T_i, calculates and displays Q_m according to both formulas, displays the difference and allows one to converge on the answer. The point at which each equation gives the same value for Q_m occurs at T_i = 329.923 K (57 °C) and Q_m = 1.34609 kg/s.

Before finding the convective heat transfer from the walls, we can sneak a look at the alternative case of the nearly closed off gate valve, with the flow rate 0.16185 instead of 0.8 of the lossless value. So Q_m = 12.892 x √[T_i - 281.35] / Ti. Combine that with Q_m = 49.5 / (T_i - 293.15), and the equilibrium state occurs at T_i = 428.744 K (156 °C) and Q_m = 0.36506 kg/s. The flow rate has decreased by only 3.687 times when there is a ratio of 4.943 between the multiplying factors, and so as expected there is some negative feedback. Turning off the flow increases the radiative heating, which boosts the temperature and the buoyancy force that drives the stack flow.

Additional losses from convection, in addition to radiation

After determining the rate of convective heat transfer, the total heat transfer rate will be some value greater than 50,000 W. The formula containing the 293.15 can be adjusted to allow for that, and the same values used as before for the formula with the 281.35 linking flue gas temperature with flow rate. (It turns out that forced convection doesn't dominate, and so the flow rate has little effect upon the convective heat transfer rate.)

The rate of convective heat transfer depends on a convective heat transfer coefficient that can be calculated according to formulas based upon "correlations" that have been experimentally determined for various situations. Firstly, heat will be transferred from the walls to the cooler air (which has also been heated through radiative heating of its water vapor, and by coming through the relatively warm oven room). Secondly, heat is transferred between corpse and air. And we need to have a value for the temperature of the air after being heated on its way through the oven room, by radiative heating, and by convective heating, in order to find out how much the corpses are going to be cooled.

And in this convective transfer, there are two types of convection: forced and natural. If we were dealing with the flow in the chimney then the convection would obviously be natural, since there's no blower or forced draft device extracting the spent gases in Crematoria IV and V. But from the point of view of the gases within the muffle, an external force is pulling them out and causing a horizontal flow across the muffle, in addition to natural convection currents within the muffle.

The standard method for determining which type of convection dominates is to compare the Reynolds (Re) and Grashof (Gr) numbers, and this test will indicate that natural convection is dominant. The ratio Gr / Re² is known as the Archimedes number. When it is between 0.1 and 10, both natural and forced convection are involved. For Archimedes numbers greater than 10, forced convection may be neglected, whereas if Re² is more than ten times Gr, forced convection is sufficiently dominant that natural convection may be neglected.

It is useful to have some values to hand for characteristics of air (the fluid) at the temperatures of interest. The "film temperature" T_f approximates the conditions within the boundary layer of relatively slow-moving fluid adjacent to the solid boundary wall; it is the arithmetic mean of the temperature of the solid boundary wall T_w and the temperature of the free-flowing stream T_∞. In our case of the muffle, T_w is taken as 850 °C (1,123.15 K), although it will decrease during evaporation and calcination. For dry air, or at low values of T_w where radiative heating of water vapor was negligible, T_∞ would be 20 °C and T_f 435 °C. However, the two predicted temperatures above due to radiative heating were 57 °C and 156 °C, increases of 37 and 136 degrees respectively. Taking the average increase at 86.5, and given that the temperature rise at half the residence time is half of that, we can take 20 + 43 = 63 °C as T_∞, and so T_f becomes 456.5 °C. Let's round these three temperatures to T_∞ = 336 K, T_f = 730 K, and T_w = 1,123 K.

Table 4 shows, for air at 336 K, 730 K and 1123 K, the absolute (or dynamic) viscosity µ in N.s/m² (or Pa.s or kg/m.s), the kinematic viscosity ν in m²/s, the density ρ in kg/m³, the Prandtl number (dimensionless), the thermal conductivity k in W/m.K, and the specific heat C_p in J/kg.K.

DryAirProperties photo DryAirProperties_zpsbe5f35ee.png

Table 4

The Prandtl number Pr is the ratio of momentum diffusivity (which is kinematic viscosity ν) to thermal diffusivity (which is α or k / (C_p x ρ), and since kinematic viscosity ν = absolute viscosity µ divided by density ρ, the Prandtl number can be found either by Pr = ν / α or by Pr = µ x C_p / k. Another dimensionless number used in natural convection is the Rayleigh number, Ra = Pr x Gr.

The Grashof number is found from Gr = g x α x ΔT x L³ / ν² where g is the gravitational acceleration (9.81 m/s²), α is (not thermal diffusivity here but) the thermal expansion coefficient, which for air at constant pressure is 1/T, with T taken as T_f = 730 K, ΔT is the temperature difference between the free-flowing fluid and the solid, L, sometimes denoted as D, is a characteristic length (m), and ν is the kinematic viscosity (m²/s). α is taken as 1/730, the reciprocal of the film temperature. ΔT is 1123 - 336 = 787 K. ν is taken at the film temperature, making it 7.076 x 10-5 m²/s. The characteristic length is not so easy to define; several alternatives have been used in the case of free convection over plates. For internal flow, if the muffle is treated as a large pipe, the length L becomes the diameter D. There are three possible cross-sections for the muffle: the 0.7 x 2 m sideways flow, the 0.7 x 0.8 m front to back flow, and the 0.8 x 2 m bottom to top flow. The best choice here was considered to be the hydraulic diameter Dh = 4A / P as calculated above at 1.396 m for 1.071 m x 2 m, which includes some additional height to allow for the volume of the ash chamber, and is not far off the mean of 0.8 and 2 m.

The Grashof number works out as 9.81 x (1/730) x (1123 - 336) x 1.396³ / (7.076x10^-5)² = 5.75x10⁹, and natural convection dominates at Reynolds numbers below 75,805. We need the gas velocity to find Re = V x Dh / ν. In the example of multiplying by 0.8 to allow for friction losses, the temperature T_i was 329.923 K (57 °C) and the mass flow rate Q_m was 1.3461 kg/s. The volumetric flow rate Q is the mass flow rate divided by the density, Q = Q_m x T_i / 353.065 = 1.3461 x 329.923 / 353.065 = 1.2579 m³/s. The gas velocity is V = Q * 0.5667 = 0.7128 m/s. Thus, the Reynolds number is 0.7128 x 1.396 / 7.076x10^-5 = 14,063, and the Archimedes number is 5.75x10⁹ / 14063² = 29.07. (The sideways gas velocity in the muffle from the chimney draft would have to be up at 3.842 m/s in order for Re = 75,805.)

In the case of the nearly turned off gate valve and multiplying by 0.16185, Q_m is down to 0.36506 kg/s and T_i is up to 428.744 K (156 °C). From Q = Q_m x T_i / 353.065, Q = 0.4433 m³/s. V becomes 0.2512 m/s. The Reynolds number decreases to 4,956, which makes the Archimedes number 234.1. Thus, not surprisingly, natural convection is even more dominant.

So in the muffle, the sideways velocity of the gases isn't so great as to be able to stop warmer gases from rising to the top. That's consistent with a compartment fire, where there is an upper layer of smoke and hot gases and the cooler air is towards the bottom. One ramification of this is that the corpses, being at the bottom of the muffles, will be hit by this relatively cool air. That's partly countered by the corpses being partly in the relatively hot boundary layer, rather than the free-flowing stream.

Another point about the no-auxiliary-fuel scenario demanded by the exterminationist legend, is that the temperatures calculated from the radiative and convective heating by the muffle walls are final gas temperatures as the gases exit into the flue duct. The gases are initially at 20 °C, and then heating occurs during the residence time that the gases are in the muffle. As the gases pass the corpses, the temperature will be less than the maximum, since they have not been heated for the full residence time. In contrast, in the semi-direct heating, the coke burns in the gasifier producing CO, the CO burns to CO₂ as it emerges into the first muffle and mixes with the combustion air, the heat released from the combustion reaction contributes to heating the corpse and the refractory walls, and there is sufficient enthalpy in the CO₂ for the excess combustion air and combustion product to reach the specified temperature.

The correlations provide the Nusselt number Nu, which represents the "effective thermal conductivity" of the fluid (the air) within the muffle. In the case where only the top surface was heated, for example, no convection currents would form because the warmer air would already be at the top and could rise no further. That would make Nu = 1, so that the "effective thermal conductivity" is no more than pure thermal conductivity. (The radiative heating of water vapor is totally separate to this.) Heated vertical surfaces, or a heated horizontal surface, contribute to convection, and Nu becomes much more than 1, with the effective thermal conductivity including the contribution from convection as well as conductivity, greatly boosting the rate of heat transfer.

The convective heat transfer coefficient h (in W/m².K) is calculated from the Nusselt number Nu according to h = Nu x k / L where k is the thermal conductivity of the fluid (W/m.K) and L is a characteristic length (m.). The thermal conductivity would be evaluated at the film temperature, the average temperature in the boundary layer. The length L should be taken in the direction of increasing thickness of the boundary layer. In this case, since natural convection dominates, the direction is up. The best choice would appear to be a little over the 800 mm height, to allow for the ash chamber, so let's make it 1 m.

Finally, when the convective heat transfer coefficient has been determined, the rate of heat transfer between fluid and solid surface is found from: q = h x A x ΔT where q is the rate of heat transfer (W), A is the area of the heat transfer surface (m²), and ΔT is the temperature difference (K) between the free-flowing stream and the solid surface. The area A is taken as 16.5 m², to give the total heat convected from the refractory walls of two muffles. The two formulas h = Nu x k / L and q = h x A x ΔT can be combined to give q = Nu x k x A x ΔT / L. From this, it is seen that for the special case of Nu = 1, the equation is the heat conduction equation.

The Rayleigh number, Ra = Pr x Gr = 0.686 x 5.75x10⁹ = 3.94x10⁹.

There are many correlations available for all sorts of situations. The Nusselt Number Correlation Classification System Homepage has documented many of these correlations, and one that is quite similar to the case of the muffle and moreover has the advantage of a relatively simple formula, is the "Natural Convection with Internal Flow on a Parallelepiped that is Horizontal with respect to gravity." A Rayleigh number of 3.94x10⁹ is within the applicable range of this correlation. The formula, by Globe and Dropkin, is:

Nu_L = 0.069 x Ra_L^1/3 x Pr^0.074

For Ra_L = 3.94x10⁹ and Pr = 0.686, Nu_L = 106.0.

In a paper by de Moura et al modelling natural convection in a "cavity parallelepiped" in which the temperature inside the cavity is initially uniform at T₀ and all six walls are "subjected to a temperature T_w, greater than T₀", their Figure 3 cites a couple of experimental correlations. Tollini (1996) gave the correlation for a parallelepiped: Nu = 0.2497Ra^0.2751, and Lin and Akins (1983) gave the correlation for a cube: Nu = 0.6Ra^0.235. At Ra_L = 3.94x10⁹ they give the predictions Nu = 108.9 and Nu = 107.9 respectively, quite consistent with the figure above. Strictly speaking, the Globe and Dropkin correlation is for a cavity heated from the bottom surface, but those from Tollini and Lin are for "all the walls" being "heated suddenly". There is little difference between the predictions, and the exterminationist allegations are favored by taking the lowest figure to reduce the rate of heat losses from the walls.

And as mentioned above, the cooler air was found to be at the bottom: "...the coldest region is always at the bottom of the cavity", although this "thermal stratification" was "not as pronounced" further away from the vertical walls, where the buoyancy-induced velocities were lower. The bones calcining in the v-shaped ash chamber are at the bottom of the cavity, and are adjacent to part-vertical, albeit oblique, walls, confirming that the air flowing at this point will be cooler than the average for the muffle.

So we take the Nusselt number as 106, and the characteristic length as 1 m. Since the thermal conductivity of air at T_f is 0.0540 W/m.K, the convective heat transfer coefficient is found from h = Nu x k / L = (106 x 0.054 / 1 =) 5.724 W/m².K. The rate of heat transfer is found from q_c = h x A x ΔT = (5.724 x 16.5 x 787 =) 74,329 W. Adding that to the 50,000 W from radiative heating of water vapor, the total becomes 124,329 W. That's 447.6 MJ per hour, so in order to obtain the same energy from burning coke at an oven efficiency of 65% and 19.5 MJ/kg, 22.95 kg/hr of coke per gasifier is needed, or 11.48 kg per muffle (or per corpse). The coke available in the exterminationist legend is 3.2 kg/hr per gasifier. Thus, losses from the stored energy in the refractory walls are (22.95 / 3.2 =) 7.172 times higher than the rate that can be supported by the exterminationist legend! And that's assuming one-hour cremations, which, if we forget for a moment that the cremations would fail, is wildly optimistic for the heat accumulator cremators scenario demanded by Hoaxer mythology, and so the gulf between propaganda and reality approaches the full order of magnitude that is indicated even by a cursory examination of the facts.

There is also the heat transferred by radiation between walls and corpses, but the rate of this transfer would become relatively low during the calcination as the temperature of the remaining tissues approaches the walls temperature. For example, if the walls are at 1,123 K, by the time the corpses are at 1,073 K we have q_rad = 2.6 m² x 5.67x10^-8 x (1123⁴ - 1073⁴) = 39,050 W for both muffles, and decreasing as corpse and wall temperatures approach each other. Then something very interesting occurs, which we'll get to later!

So, adjusting the above formula which was for radiation without convection, the temperature rise of the air ΔT = T_i - 293.15 = 124,329 / (1010 x Q_m) = 123.1 / Q_m, where Q_m is the "Mass flow rate per muffle pair" in kg/s in Table 3 above, which, without allowing for any losses due to friction, etc., is given by:
Q_m = 79.653 x √[T_i - 281.35] / T_i. That must be multiplied by either 0.8 or 0.16185, so for the first case we have: Q_m = 63.722 x √[T_i - 281.35] / T_i.

ΔT = T_i - 293.15 = 123.1 / Q_m, and so Q_m = 123.1 / (T_i - 293.15)

Now the equilibrium state should have Q_m = 123.1 / (T_i - 293.15) and Q_m = 63.722 x √[T_i - 281.35] / T_i. The point at which each equation gives the same value for Q_m occurs at T_i = 369.237 K (96 °C) and Q_m = 1.61788 kg/s.

In the alternative case of the nearly closed off gate valve, with the flow rate 0.16185 instead of 0.8 of the lossless value, we have Q_m = 12.892 x √[T_i - 281.35] / Ti. Combine that with Q_m = 123.1 / (T_i - 293.15), and the equilibrium state occurs at T_i = 614.625 K (341 °C) and Q_m = 0.38292 kg/s.

In reality, the radiative heating of water vapor would heat the air uniformly, whereas the convective heating would result in hot boundary layers adjacent to the walls, with the upper layer being the hottest, and with the remainder only subject to the radiative heating. But to favor the exterminationist legend, we will suppose that the air flowing past the corpses at the bottom is the temperature that the air could be heated to, if all heated uniformly, and all having already received the full quantity of heat for the full residence time as it passes the corpses. The buoyancy force or stack effect from a lower density is essentially determined by the average gas temperature, and is almost the same whether or not the gas is isothermal.

It is this second version, with the nearly closed off gate valve, that is most favorable both to the actual cremations that occurred with some 35 kg/hr of coke per gasifier and the Hoaxers' fantasy scenario of a massive lean burn fuel economy drive in which 1.3 million corpses were allegedly so efficiently cremated using a mere 1.6 kg of coke per corpse that they became, "in a sense, invisible." It works so well with the actual reality of up to 170,000 deaths at Auschwitz-Birkenau, almost all from natural causes, with the ovens consuming somewhere in the order of 20 kg of coke per corpse, because such conditions allow for gas temperatures of 850 °C which are ideal for calcination, and the process satisfies the law of conservation of energy. The Hoaxer scenario is not feasible either way, but by economising on the gas flow rate the gulf between the real world and Hoaxer fantasy narrows marginally (albeit still a giant chasm!).

Note that the gas temperature even in the most favorable case of 341 °C is well below the absolute minimum of 500 °C for calcining bones, which even at 500 °C takes seven to eight hours! And this assumes the refractory walls have an emissivity of 1; a lower emissivity will result in a lower gas temperature. In any case, the 341 °C is based on a refractory wall surface temperature of 850 °C. The refractory temperature will decrease as soon as the walls are transferring their heat to the corpses, and the temperature of the exposed surface - which is a determinant of the radiative transfer rate and the convective transfer rate - will drop relatively rapidly.

If the heat transfer rate is lower than predicted above, then the air temperature will be lower and failure is even more assured at the calcination stage, if the cremation gets that far. If the heat transfer rate is higher, then the deficit between losses and the coke supply available in the Hoaxer model becomes even more pronounced, and the temperature of the refractory walls declines even more rapidly.

During the calcination, the refractory material is losing energy at a rate of ~124,000 W (plus heat transferred to the corpses). Even under ideal conditions, calcining the bones is known to take 20 to 30 minutes, before increasing to seven to eight hours at 500 °C. A transfer rate of 124,000 W over 25 minutes amounts to 186 MJ, but the rate would be expected to decrease somewhat as the temperature drops.

In the section above about the evaporation stage, it was shown how the surface temperature and the quantity of energy transferred from a plane wall could be calculated, given two dimensionless variables: the Biot number and the Fourier number. During calcination, the heat lost from the refractory material is mostly by convection, and partly by radiation. When we adjust the convective heat transfer coefficient h of 5.724 W/m².K by a factor of 124329 / 74329 to allow for the extra 50,000 W from radiative transfer, h becomes 9.574 W/m².K. The Biot number is h x L / k, where L for the refractory material is 0.122 m and k is 0.767 W/m.K, and so Bi = 1.523. And in this calcination case, since the air inlets need to be open, the refractory temperature and the corpses would eventually cool to the temperature of the incoming air at 20 °C. Thus, the initial condition assumes the refractory material to average 800 °C, at which the surplus energy in excess of 20 °C is 4,014 kg x 930 J/kg.K x 780 K = 2,912 MJ. It would be interesting to find how much energy is lost from the walls, and how much the surface temperature will drop, after a time of 25 minutes.

Since a Fourier number of 1 corresponds to 36,091 seconds, Fo = 0.04156 corresponds to 25 minutes. The combination Bi = 1.523, Fo = 0.04156, predicts the proportion of energy transferred is 0.05193, which is (0.05193 x 2912 =) 151.2 MJ. The dimensionless temperature of the exposed surface is 0.7274, which works out at 20 + 0.7274 x 780 = 587 °C. Under ideal conditions, if gas temperatures are maintained at 850 °C, say, a calcination time of 25 minutes would not be unreasonable. However, in the exterminationist lean burn heat accumulator cremations, conditions are anything but ideal; the gas temperature is only 341 °C at the start. After 25 minutes, even the walls' surface temperature is down to under 600 °C, and by this time the gas temperature will be well under 341 °C. The bones would be at an intermediate temperature between the walls and gas temperature. After 25 minutes, the system would continue to cool.

If the Germans had somehow managed to run the gasifiers at 3.2 kg/hr of coke per gasifier, then at 65% oven efficiency and 19.5 MJ/kg, that provides 26 MJ in 25 minutes, so the 151.2 MJ deficit has been reduced to 125.2 MJ; which is a fairly insignificant 17.2% reduction. If we pretend that the calcination could somehow work at gas temperatures around 300 °C or lower, with the walls at 500 to 600 °C, by the time we allow for seven-hour cremations, the gasifiers would have to be run at 0.457 kg/hr of coke in order to maintain the required 1.6 kg of coke per corpse. In any case, the idea that the gasifiers were run at 3.2 kg/hr of coke - or lower! - can already be discounted as mentioned above by the lack of any evidence for adaptations to the ovens in which additional small inlets, smaller than the standard type door, would have had to have been built into all the gasifiers so that they could still run with a scarcity of oxygen at such a low coke burning rate. And by the failure of Prüfer and Schultze to say a word about any such adaptations, when Prüfer had 'confessed' to 'knowing' that innocent people were being "liquidated" in Auschwitz "gas chambers", and Schultze 'confessed' to being aware of 'killings' at Auschwitz, of people whom he believed to be "criminals".

So could the gate valve have been turned off even more, further reducing the flow, and helping to increase the temperature and reduce losses in the exterminationist scenario? The air flow rate has already been reduced to 379 g/s, which is below the minimum for two corpses. Our estimate above concluded 376 g/s of air for a single corpse. Beek recommended 3,470 lb/hr, which is 437.2 g/s, for one corpse with a coffin, excluding the natural gas. Turning the combustion air down further would leave the corpses with a greater scarcity of combustion air during the exothermic stage, so that the corpses would gasify rather than combust. Since the corpses are the only remaining heat source in the no-auxiliary-fuel scenario, the conspirators could not afford to waste any more of that energy, which would certainly happen in the region of 100-200 g/s for two corpses.

At the available 3.2 kg/coke per hour per gasifier, the total flow rate exiting the ash chamber of the second muffle could be no greater than 24.1 g/s in order to sustain a gas temperature of 850 °C. Alternatively, it could be no more than 38.2 g/s to support a temperature of 600 °C. Under the 35 kg/hr of coke per gasifier regime, it's very feasible that each gate valve could have been carefully adjusted to the optimum setting that would work throughout the cremation cycle, and once a suitable setting was found, it would not be changed until some major maintenance was performed. But under the no-auxiliary fuel scenario, it would be absurd to have the Sonderkommando frequently adjusting the gate valves between very nearly closed and even more very nearly closed, according to whether a cremation was in the fat burning or calcination phase. The eight-muffle oven had only one gate valve for every four muffles, and given that some bodies are much easier to cremate than others, four cremations would soon go out of sync. And the possibility that new, tiny inlet doors were built into every muffle, just as a massive "extermination" program began, when Prüfer and Schultze did not breathe a word about any such adaptations, and there is not the slightest evidence for any such adaptations, is easily dismissed.

The fat burning exothermic phase, at best, is only going to be able to restore the refractory walls to the equilibrium state that was obtained after preheating, with the surface temperature around 850 °C (which is already well over Schläpfer's 600 °C, so 850 °C is rather optimistic!) and the thermal gradient having a satisfactory negative slope right along to the outer surface of the normal brickwork. If the first cremations make it as far as the calcination phase before failing, then when the Sonderkommando attempt to cremate a second set of corpses, they are going to be starting out from a lower initial temperature. The subsequent attempts will probably not even make it to the fat burning phase, and failure is even more assured.

Why the exterminationist thesis requires suspension of the law of conservation of energy

It's now time to deliver the coup de grâce to Hoaxer mythology. For modelling the convective heat transfer between air and corpse (or bones), we can use the Morgan correlation, displayed at the Nusselt Number Correlation Classification System Homepage as "Natural Convection with External Flow on a Cylinder that is Horizontal with respect to Gravity". For Rayleigh numbers between 10⁴ and 10⁷, the Nusselt number is simply:
Nu_D = h x D / k = 0.48 x Ra_D^0.25

(The formula can be shown with a bar over the top of Nu and h, to denote that those are the averaged out values for Nu and h, which is what we need to know. The D subscript shows that the Ra and Nu numbers apply to a characteristic length D.)

In this case of the calcining bones in the muffle, the Rayleigh number comes within those limits; the correlation includes a table showing which values to use for the coefficient C, in this case 0.480, and the index n, in this case 0.250, for other ranges of Ra numbers. There is also a more complex formula "for a wide Rayleigh number range". At the Rayleigh number of interest, its predicted Nusselt number is within 7% of the simpler formula's prediction. These correlations are only approximations for engineering purposes, and even at best, would not be expected to have an accuracy better than about 20%. Changing the assumed values for variables such as the diameter D do not have as much effect on the Nusselt number as one might expect. In any case, as we shall see, the value of the convective heat transfer coefficient h doesn't actually change the conclusion. It could be as low as 0.001 W/m².K, and the cremation would still fail. But curious minds will want to know what happens, such as how the temperature of the remaining organic material will change over time. Those who run the program provided will be able to assess the effects of changing various assumed values.

The Grashof number is Gr = g x α x ΔT x D³ / ν². This is almost the same as before, except the diameter D has replaced the length L. We'll use D = 0.1 m as the diameter of the remains of the corpse, but also consider how other values affect the results. g remains at 9.81 m/s². In order to find the other variables, we need the temperatures. The temperature T_∞ of the air flowing past the corpse is higher than 20 C, because of radiative and convective transfer from the refractory walls. In order to make the model as favorable as possible to the exterminationist allegations, we'll take the "best" case as described above, where the gate valve is almost closed off, and the walls heat the incoming air to a temperature of T_i = 614.625 K (341 °C) at a mass flow rate of Q_m = 0.38292 kg/s. That T_i is supposed to be the final temperature as the gases exit the second muffle after having been fully heated by radiation (to the water vapor) and convection, whereas the air flowing past the corpse is at some lower temperature. Nevertheless, let's suppose T_∞ is that T_i, at 614.625 K. Moreover, to simplify the computations, we'll suppose that T_∞ remains at 614.625 K rather than recalculating it at each time step of a second, when in fact it would decrease along with the wall temperature.

Moreover, we'll simplify the computations by treating the wall as if its Biot number is infinitely low, so that the "lumped capacitance method" can be used, and the walls' surface temperature is assumed to drop by 1 °C for every (4,014 kg x 930 J/kg.K =) 3,733,020 J transferred from it. Of course, in reality, the Biot number is probably about 1.5, and the exposed surface temperature would decay relatively rapidly. Moreover, we'll simplify the computations by assuming a constant 5,000 W in losses from the walls to the air (we also count the radiative transfer from walls to corpses), when in fact as calculated above, those losses would initially be ~124,000 W, and then decrease with the wall temperature, so that after 25 minutes instead of 186 MJ, it would amount to 151.2 MJ, which is an average transfer rate of 100,800 W (and still much more than 5,000 W!).

The temperature T_c of the corpse or bones is assumed initially at t = 0 seconds to be 553.15 K (280 °C), the auto-ignition temperature of the fats. The time t = 0 seconds is assumed to be the point where the fats, proteins and carbohydrates are sufficiently consumed that the heat released from any remaining combustibles becomes lower than the heat absorbed by the endothermic calcining of the bones, which includes recrystallizing the apatite and decomposing the calcium carbonate into calcium oxide and carbon dioxide; in other words, the endothermic calcination phase takes over from the exothermic burning of organic material. It makes no difference to the outcome if T_c is assumed to be higher at t = 0; in fact, the time at which the corpse temperature peaks and starts to fall is brought forward. With an initial T_c = 1,073.15 K (800 °C), it takes 3.183 minutes, as opposed to 5.733 minutes for T_c = 553.15 K.

The film temperature T_f is the mean of the corpse temperature T_c and T_∞, the temperature of the free-flowing stream of air outside the boundary layer between that and the corpse remains. The thermal expansion coefficient α of the air is the reciprocal of the film temperature T_f, and ΔT is the difference T_c - T_∞. The kinematic viscosity ν of the air would be taken at the film temperature. We recalculate the film temperature and ΔT with each time step, to be used for finding the Grashof number. However, a number of simplifications have already biased the model massively in favor of the Hoaxer allegations, and it is not worth developing formulas to recalculate the kinematic viscosity, thermal conductivity, and Prandtl number at each step. The corpse temperature will typically be in the region of 1,073.15 K (800 °C), which, given a temperature T_∞ of 614.625 K, would make the film temperature T_f = 843.89 K. Let's round it to 844 K. At that temperature, air has a kinematic viscosity ν of 8.959x10^-5 m²/s, a thermal conductivity k of 0.0600 W/m.K, and a Prandtl number Pr of 0.693.

So from Gr = g x α x ΔT x D³ / ν², at T_c = 1,073.375 K, T_f = 844 K, and T_∞ = 614.625 K, Gr = 9.81 x (1/844) x (1073.375 - 614.625) x 0.1³ / (8.959x10^-5)² = 664,330. The Rayleigh number is Gr x Pr = 664330 x 0.693 = 460,381. From the Morgan correlation, the Nusselt number is:
Nu_D = 0.48 x Ra_D^0.25 = 12.50. The convective heat transfer coefficient is h = Nu_D x k / D, which is 12.5 x 0.06 / 0.1 = 7.5 W/m².K.

The rate of convective heat transfer between corpse and air is q_conv = h x A_conv x (T_c - T_∞). At this stage, with nearly all the combustible organic material consumed, we take the remaining mass at 10 kg per corpse. 80% of the bone mass in the adult human skeleton is comprised of cortical (or compact) tissue, with a specific heat of 1,313 J/kg.K. Cancellous (or trabecular) bone tissue has a specific heat of 2,274 J/kg.K, so we will take the specific heat of the remaining organic material as 1,500 J/kg.K.

The area for radiative transfer purposes is 1.3 m² out of the total 1.8 m², based on the view factor from the walls, but for convective transfer purposes this would be closer to the 1.8 m². We'll suppose A_conv = 1.6 m², which makes some deduction for the area in contact with the bottom surface. By the time the bones are exposed, the total surface area for convective transfer purposes might be considered to have increased. The beagle, for example, has a total bone surface estimated at 2.9 m², compared to the 1.8 m² of the intact human body. However, the area "seen" by the oven walls, if anything, is going to be less than the original 1.3 m² for the intact corpse. Nevertheless, let's stick with A_conv = 1.6 m² and A_rad = 1.3 m². Raising A_conv would not help Hoaxer claims, but the effect of changing these values is marginal, and will certainly not change the outcome. In fact, apart from lies, lies, and more lies, indoctrination, laws restricting free speech, book burnings, bombs, thugs, a suspension of the law of conservation of energy, or variations in the fundamental physical constants, there isn't really anything that can save exterminationist allegations!

The model treats the pair of linked muffles as a single system; we're using 4,014 kg as the mass of refractory material for calculating the change in wall temperature. The cremations would still fail if we did this but did not double the 10 kg, 1.3 m² and 1.6 m² per corpse. However, so many concessions have already been made, and there is no reduction in complexity to be gained from failing to double those values.

So the program (download calcin1code.htm; see above for how to run) is initialised with the following variables: ν = 8.959x10^-5 m²/s, k = 0.06 W/m.K, Pr = 0.693, D = 0.1 m, A_conv = 3.2 m², A_rad = 2.6 m², g = 9.81 m/s², T_∞ = 614.625 K, T_c = 553.15 K, T_w = 1,123.15 K, m_corpses = 20 kg, and cp_corpses = 1,600 J/kg.K. For each time step of one second, the Grashof and Rayleigh numbers are found (α and ΔT are recalculated, ν remains at the typical film temperature value), the convective heat transfer coefficient h is calculated, followed by the rate of convective transfer from corpses to air, the rate of radiative transfer from walls to corpses, the corpses' temperature based on the net transfer to the corpses, and the walls temperature based on the losses from the walls. The program displays the Nusselt number, heat transfer coefficient, temperatures of corpses and walls, etc., and defaults to stepping forward when a key is depressed, allowing one to pause, and to run through the results at a speed that allows for easy viewing of the figures.

The corpses start from T_c = 553.15 K at time t = 0; setting this initial value higher would shorten the time before T_c peaks and inevitably starts to decrease. At first, the rate of convective transfer, corpses to air, is negative; i.e., the corpse temperature is lower than the surrounding air, so the corpses are absorbing heat by convection, as well as by radiation from the walls. The rate of radiative transfer, walls to corpses, starts at more than 200,000 W, declining as the corpse temperature rises towards the wall temperature. The corpse temperature is increasing at nearly 7 °C per second, and it only takes 11 seconds for the corpse temperature to go above the air temperature T_∞. At that point the convective transfer rate, corpses to air, turns positive, indicating that the corpses are transferring heat to the air. So far, the corpses are receiving very much more by radiation from the walls than they are giving up by convection to the air, and the corpse temperature continues to increase. However, the rate of increase is continually decreasing.

As the corpse temperature increases, the rate of heat loss to the air by convection increases, whilst the rate of absorption from the walls decreases. The net transfer to the corpses decreases. Finally, at 5.683 minutes (341 seconds), the net transfer to the corpses turns negative, as the corpses are losing 12,932 W to the air but receiving only 12,930 W from the walls. The corpse temperature is 827.83 °C and the wall temperature is 843.90 °C. At 10.8 minutes, the net transfer to corpses hits a negative peak at -152.6559W, with the corpse temperature at 826.55 °C and the wall temperature at 842.44 °C. Thereafter, the magnitude of the net transfer to corpses remains around that rate, declining very slowly. At t = 30 minutes, the net transfer to the corpses is still at -151.2 W. The corpse temperature is 821.08 °C and the wall temperature is 836.99 °C. So the corpse temperature remains about 16 °C below the wall temperature, as it tracks the decline in wall temperature.

Calcining of bone is an endothermic process, requiring an absorption of heat into the organic material. However, in the calcination stage of the cremation, the heat accumulator cremation scenario demanded by Hoaxer mythology can only support a net transfer of heat to the corpses for less than six minutes, which is way below the minimum time for calcining bones even under optimum conditions such as an air supply that is heated to 850 °C. If the Germans had been capable of calcining bones whilst those bones were net emitters of heat, the Germans would have been capable of circumventing the law of conservation of energy, which is equivalent to building a perpetual motion motion!

Of course, this simplified model massively favors the Hoaxer allegations. In reality, the walls temperature would decline much more rapidly, the air temperature would also drop in line with the reduced transfer by radiation and convection from the accumulated heat in the walls, and the corpses would cool much more rapidly. The Germans would have ended up with 1.3 million skulls, 2.6 million femurs, 31.2 million ribs, etc., that were difficult to crush, leaving so much physical evidence of genocide that they might as well have taken photos and film footage of the "gas chambers", conducted autopsies on the "gassed" victims proving death by cyanide poisoning, and ordered someone to fly with it to Scotland. That's before we count the fact that the ovens would need to be in operation for more than 42 (forty-two) hours per day, the firebricks would need to survive for 25,000 cremations per muffle when the upper limit was around 3,000, and it would have been absurd for the Germans to have used tons of Zyklon B in delousing chambers to save their prisoners' lives by killing typhus lice, at the exact same time and place that they were allegedly using kilograms of that very same Zyklon B to kill their prisoners.

Can anyone, even in their wildest fantasies, imagine that an evil regime bent on industrialized mass murder would choose merely to partially cremate the victims, leaving a tremendous amount of physical evidence to be discovered? Especially when this very same regime is alleged to have become so panicky about the possibility of mass graves being discovered at Treblinka that they are alleged to have dug up 900,000 bodies and burnt them all in open-air cremations using green (wet) wood as fuel, all in the space of seven months!

A longer version of the program (download calcin2code.htm) includes a solution to the cooling of a plane wall problem, showing more accurately how the wall surface would cool during calcination. Most of the time, this predicted surface temperature is not only well below the other predicted surface temperature based on the "lumped capacitance" method of an infinitely low Biot number, but the more accurately predicted surface temperature is well below the predicted corpse temperature that was based on the "lumped capacitance" prediction. It shows how these simplifications are so overwhelmingly in favor of the exterminationist allegations. And it doesn't even allow for cooling of the air hitting the corpse. Of course, the heat accumulated in the refractory material is the only source of energy for heating that air, and as the wall surface cools, the mean air temperature cools towards the incoming 20 °C.

Let's suppose we chose a value of 0.01 m instead of 0.1 m for D. In the Grashof number formula (Gr = g x α x ΔT x D³ / ν²,), the Grashof number is proportional to D³, so it might be expected that lowering the value of D would greatly lower the rate of convective heat transfer. To recap, in the original calculation, at T_c = 1,073.375 K, T_f = 844 K, and T_∞ = 614.625 K, Gr = 9.81 x (1/844) x (1073.375 - 614.625) x 0.1³ / (8.959x10^-5)² = 664,330. The Rayleigh number is Gr x Pr = 664330 x 0.693 = 460,381. From the Morgan correlation, the Nusselt number is:
Nu_D = 0.48 x Ra_D^0.25 = 12.50. The convective heat transfer coefficient is h = Nu_D x k / D, which is 12.5 x 0.06 / 0.1 = 7.5 W/m².K.

So we change D to 0.01 m, and: Gr = 9.81 x (1/844) x (1073.375 - 614.625) x 0.01³ / (8.959x10^-5)² = 664.33; a thousand-fold reduction as expected. The Rayleigh number is Gr x Pr = 664.33 x 0.693 = 460.38. In the Morgan correlation, given that Ra_D is now in the range 10² to 10⁴ instead of 10⁴ to 10⁷, alternative values of the C coefficient and n index are used (as in the table in the correlation), and so the Nusselt number is:
Nu_D = 0.85 x Ra_D^0.188 = 2.692. The convective heat transfer coefficient is h = Nu_D x k / D, which is 2.692 x 0.06 / 0.01 = 16.15 W/m².K; more than twice as much as before!

Suppose the convective heat transfer coefficient h is very, very low. Let's say it is only 0.01 W/m².K. Take out the "REM***" so that h = 0.01 overrides the previously calculated h value in the program, and it takes until t = 6.517 minutes (391 seconds) before the corpse temperature starts to decrease and the net rate of transfer to the corpses turns negative. The wall temperature continues to decay; the effect of reducing h is that the corpse approaches it much more closely before reaching the equilibrium point; in this case, to within about 0.018 °C, as opposed to the 16 °C with the more realistic value of h. After changing h by such a large amount, it takes only 50 seconds longer for the corpses to become net emitters of heat. (Or try setting h to -1. The time only increases by another 15 seconds, to 6.767 minutes!) Bones cannot be calcined in six or seven minutes. In any case, that simplified prediction with h = 0.01 W/m².K has the wall surface temperature at 844.635 °C at t = 6.517 minutes, with the corpse temperature at 844.617 °C. Using the more exact plane wall solution for the surface temperature, the prediction for that time is 720.15 °C, which still overestimates the refractory surface temperature, given that the Biot number hasn't been adjusted up to compensate for radiative transfer accounting for a significant proportion of the wall losses. The emissivity is still assumed to be 1, to favor the Hoaxer model, and the reduction in air temperature as the walls cool down has not even been taken into account.

The system needs an auxiliary power source, in order to maintain the wall surface temperature and the air temperature, so that the corpses can be net absorbers of heat during the calcining. And that is not provided by the Hoaxer scenario, which doesn't even have enough fuel to heat the air for more than 2.4 minutes, even if we discount the fuel required for preheating.

Conductive losses

For the sake of completeness, we can include details of conductive losses through the muffle walls, to show how that compares with the available 1.6 kg of coke per corpse in the exterminationist scenario. The double-muffle oven had 15 cm of refractory brick, 7 cm of insulating brick, and 20 cm of ordinary brick; the construction of another oven shown in Prof. Schläpfer's diagram referred to above was very similar, and so we'll use this as a basis for specifications of the eight-muffle oven. An individual thermal conductance is:
C_n = k_n / x_n
where C_n is the conductance in W/m².K, k_n is the thermal conductivity in W/m.K, and x_n is the thickness of the conductance in meters. Conductors in series are like resistors in parallel; the overall conductance, often denoted as U, is the reciprocal of the sum of the reciprocals of the individual conductances:
1 / U = x₁ / k₁ + x₂ / k₂ + x₃ / k₃ ... = 1 / C₁ + 1 / C₂ + 1 / C₃ ...

Taking the figures in Schläpfer's diagram, Document 48 on p. 727, Auschwitz: The Case for Sanity, he writes thermal conductivity (lambda) as 0.66 for the refractory brick, 0.12 for the insulating brick, and 0.4 for the normal brickwork. From the values, and from his use of kcal/min on his radiation transfer diagram, his units are apparently kcal/m.hr.°C. The conversion from kcal/m.hr.°C to W/m.K is 4184/3600 = 1.162, so in W/m.K that's 0.767 for the refractory brick, 0.139 for the insulating brick, and 0.465 for the ordinary brick.

So we have: 1 / U = 0.15 / 0.767 + 0.07 / 0.139 + 0.2 / 0.465 = 1.129, and so U = 0.886 W/m².K. (With the total thickness at 0.42 m, the average thermal conductivity is k = U x Δx = 0.886 x 0.42 = 0.372 W/m.K.) The rate of heat conducted through the walls, Q, is given by:
Q = k x A x ΔT / Δx = U x A x ΔT = 0.886 x A x ΔT

Referring to the above analysis of the likely distribution of refractory material in the eight-muffle oven, if we exclude the internal walls, that leaves: Outer muffle:- Exterior side, 2 x 0.79 m = 1.58 m². Front, 0.79 x 0.7 + 0.192 = 0.745 m². Top, 2 x 1.1 m = 2.2 m². Bottom, 2 x 0.7 m = 1.4 m². Total, outer muffle, 5.925 m². Inner muffle:- Front, 0.79 x 0.7 + 0.192 m = 0.745 m². Top, 2 x 1.1 m = 2.2 m². Bottom, 2 x 0.7 m = 1.4 m². Total, inner muffle, 4.345 m². Average area of exterior walls per muffle = 5.135 m², or 10.27 m² for a pair of linked muffles.

(We suppose that all muffles are operating, so there are no losses through internal partitions into an unheated muffle and out through exterior walls.) Taking the pair of muffles together, the conductive losses are:
Q = 0.886 x 10.27 m² x ΔT = 9.1 x ΔT

If the cold side is 20 °C and the inside of the refractory brick is heated to 850 °C, then ΔT = 830 K and the conductive loss is at a rate of 7,553 W, which amounts to 27.19 MJ/hr. Assuming 65% oven efficiency, the coke yields 0.65 x 30 = 19.5 MJ/kg, and so the conductive losses require 1.39 kg of coke per hour, compared to the 3.2 kg of coke that Hoaxers have available (for two muffles and two corpses), which leaves ~0.9 kg of coke per corpse. That neglects the higher rate of loss through the front, which doesn't have all the insulating bricks and normal bricks in order to allow access, and has radiative losses out through the air inlet during calcining. And that assumes one-hour cremations, which would not be possible given the available fuel, even if we pretend the cremations would have succeeded when in fact they would have failed. The conductive loss through the walls is dwarfed by the convective and radiative losses to the air that must flow through the system in the calcining stage. However, the conductive loss remains at all times, only decreasing as the refractory temperature decreases.

Conclusion

In Hoaxer dreamland, apart from the prisoners who did die from natural causes at Auschwitz-Birkenau, there are more than a million additional prisoners who are murdered, cremated with non-existent fuel or burned by themselves when bodies cannot burn by themselves, and kept off the registers and the death books to conceal the evidence, the Germans are devious enough to fake registered deaths under the age of 10 and over the age of 80, and to send a 15-year-old Jewish girl with scabies from Auschwitz to Bergen-Belsen, to make it seem like these people weren't murdered routinely, there are gas chambers that worked when they could not have worked and left no cyanide traces when they should have, there are delousing chambers with massive residues of cyanide on their walls that were used to save prisoners' lives at the very same time and place that homicidal gas chambers were used to kill them with cyanide that didn't leave a trace, amateur woodcutters in a death camp and slave labor camp are able to achieve 81 times the productivity of professional woodcutters in peacetime, there is an extermination program that was communicated by telepathy, there are secret codes and euphemisms that were never cracked by the Allies until it was too late such as "special treatment" for extermination, it's just supposed to be a coincidence that claims of death camps in Germany proper, four million killed at Auschwitz, Jews made into soap and lampshades, murder by quicklime, vacuum chambers, electric plates, pedal-operated brain-bashing machines, etc., all turned out to be a pack of lies, and it's another string of coincidences that the Germans destroyed all the evidence of an extermination program and systematically eradicated the witnesses, that not a single German thought to take a photograph or film of a gas chamber that he would later be able to sell for a fortune, that people were beaten up and autopsies conducted to find out how they died but no autopsies were conducted on any gassed victims, that people making documentaries to inform the world about the atrocities also made schoolgirl howlers that they should not have made, that people informing the world about gassings with gasoline exhaust fumes incorrectly believed it to be Diesel exhaust fumes and incorrectly testified to people's skin turning blue until skeptics demonstrated that they were wrong, that the only evidence for extermination consists of forced confessions, documents that were falsified or are open to interpretation, and eyewitness testimony from those under peer pressure or financial incentive to testify for the exterminationist thesis, that a group of Jewish fanatics gained immense wealth and political power as a consequence of the extermination program, that Jewish fanatics have alleged holocausts and exterminations against them since time immemorial, that Rabbi Stephen Wise spoke of "six million" dying Jews in 1900 and was among the first to make allegations in 1942 of an extermination program, that his allegation of mass murder by firing squad was quickly abandoned for mass murder by gas chambers as soon as Germany's accusers became aware of the opportunity of claiming delousing chambers as gas chambers, and that people who point out the absurdities, impossibilities and lack of evidence for an extermination program are vilified, beaten up, blown up, fined, jailed, and evidence presented in their defense at trial is either ignored or classed as illegal.

The choice is between the Hoaxer model, which requires that we revise the laws of nature and posits that revisionists lie in order to have their careers ruined, face jail sentences or heavy fines, get blown up / beaten up, etc., and the revisionist model, in which witnesses lie for money, because of peer pressure, because they were brainwashed and confused, or to try to avoid further torture, and is consistent with our scientific and natural law. It is the physical impossibility of Hoaxer claims that enable the rest of us to know with certainty that "eyewitnesses" were either lying, mistaken, brainwashed or confused. And the fact that most people - including Jews - are not lying but are relaying what they sincerely but erroneously perceive as 'truth' after decades of indoctrination, is why there should be no backlash against any ethnic or religious group, when the entire flimsy house of cards is blown down by a tidal wave of reality.

Hoaxers have to trick newcomers into imagining that those who debunk the Hoaxers' preposterous, physically impossible yarn of mass exterminations are doing it not because they love truth and justice, but because they "hate" Jews for no reason at all, or they're "neo-Nazis", etc. The fact is that whenever there are two sides at war with each other, each side will exaggerate the other's losses and play down their own. If there really were all these "neo-Nazis" and "anti-Semites" running around, and if there really had been a "Holocaust" in which six million Jews were murdered in gas chambers, the "neo-Nazis" and "anti-Semites" (who would perceive themselves as being in some sort of 'war' against the Jews) wouldn't be denying that six million were murdered, and writing long articles to explain why not. They'd be boasting about it, joking about it, and exaggerating the numbers. These "neo-Nazis" would be making comments such as "Hitler killed twelve million Jews, and they all richly deserved it", whilst high-fiving, taking "selfies" whilst flicking lighters with photos of the Topf ovens in the background, hugging each other, telling macabre jokes, smiling, etc., in celebration, rather in the manner of the "dancing Israelis", before the second plane crashed into the South Tower. Instead, historians, chemists and patriots risk having their car blown up, their home pipe-bombed, their jaw broken, years in jail, massive legal costs, etc., merely for the 'crime' of telling the truth!

The Hoaxer strategy relies upon the fact that years of mainstream media brainwashing has led people to believe that Hitler and the 'Nazis' were "anti-Semites" and evil monsters who systematically "exterminated" "six million" Jews in "gas chambers" because they hated Jews for no reason at all. People who subscribe to the "Holocaust" religion do so because they obtain all their 'information' about it from Hoaxer sources - mainstream media that is dominated by Zionist Jews, conformist 'historians' who were either brainwashed themselves or soon learned what was best for their careers, and "Holocaust survivors" with sob stories who soon learned what a racket the Holohoax is. Obtaining 'information' from a single, biased source is recognized as "crippled epistemology". Meanwhile, those who have taken the time to study the facts and have learned that the "Holocaust" fable is a tissue of lies know that WWII - far from being a "good" war to fight the "evil" 'Nazis' and save Jews from being killed - was actually instigated for political and business purposes by Zionist Jews and their lackeys such as Britain's biggest ever traitor and war criminal Winston Churchill, who has the blood of tens of millions on his hands, yet ironically is supposed to be a hero. Churchill and the Allied attackers escalated a little local war that would have killed no more than thousands (which is much less than the death toll of warmongers Bush, Blair et al in purely aggressive wars for profit and power launched on a false prospectus) into a world war that slaughtered tens of millions. Churchill should have been tried and executed for crimes against humanity. But there is still time to bring Bush and Blair to justice.

Hoaxers would have people believe that revisionists are all "neo-Nazis" or "anti-Semites" who lie, and "deny" "the Holocaust" because they are "haters" who want to rehabilitate Hitler. In fact, revisionists are ordinary people from all over the political spectrum with a love of truth and justice, who looked into the 'evidence' for "the Holocaust" and found it wanting.

Humans will lie for power and profit, but the laws of thermodynamics and thermochemistry cannot be suspended. The forensic evidence does not lie, whereas the word of liars is hearsay that cannot be substantiated. It doesn't matter whether there are six, six thousand or six million eyewitnesses who make claims that cannot possibly be true, or how many Hollywood movies have been made, or how many newspaper opinion pieces have been written; they are still drowned out by the laws of nature. In the case of the "Holocaust", what we have is thousands of liars whose lies contradict each other, and millions of dupes who have been brainwashed by the lies.

The "Holocaust" is simply a new religion that was fabricated in the 20^th century for the benefit of the ruling elite. It exploits the fact that many people have a psychological need to believe that the world is more complex than it actually is, with miracles happening such as bodies that burn with negligible fuel and about ten times quicker than dictated by the laws of thermodynamics, and Germans who inexplicably use 0.1% of their Zyklon B to kill their prisoners whilst using 99.9% of it to save their prisoners' lives. Religious fables such as the "Holocaust" require a suspension of disbelief, a wilful disregard of logic, and a rejection of natural law.

When justice is finally done, and the Hoaxers are stripped of their ill-gotten gains and exposed as the lying, snivelling charlatans that they are, there are several groups who should have priority claim upon the massive fortunes to be redistributed: revisionists who have been jailed, fined, sued, beaten up, etc., for telling the truth, Germans whose nation has been the victim of a despicable libel and forced to pay "reparations" for a crime of which she was entirely innocent, Palestinians whose land has been turned by foreign, Asiatic settlers into a racist, apartheid State that treats those indigenous Palestinians as second-class citizens or worse. But we mustn't forget the millions of ordinary, innocent Jews who were also duped by the scam. Those of us who aren't part of a minority group who for decades have labored under the misapprehension that they'd been the victim of a terrible, systematic extermination, in which millions of its members were murdered in cold blood, and who lived in constant fear that because such an atrocity had already happened once it might happen again, will never begin to imagine their fear and anguish. Hoaxers must also compensate the Jewish people for their mental suffering.

Religions are supposed to induce people into doing the right thing, and to provide psychological comfort in an imperfect, often unfair world. The "Holocaust" religion served to enrich and empower its promoters, whilst financially and psychologically impoverishing its adherents. It's time for "the Holocaust" to join the flat Earth, the "Donation of Constantine", and the geocentric solar system in the dustbin of history.

Continue to Volume Three: Israel's 9/11 False-Flag

Return to Volume One: The Protocols of Joly